드디어 푸아송 분포까지 왔다. 푸아송 분포는 확률론과 수리통계를 배울 때 갑툭튀하여 수많은 중도포기자를 발생시키는 데 악명이 높다. 그 이유는 분포를 이해하는 데 핵심사항인 확률변수 ($X$)의 정의와 모수 ($\lambda$)의 정의를 잘 모르는 것일 수도 있고, 난해한 PMF 때문일 수도 있다. 이번 글에서는 푸아송 분포의 모수와 확률변수를 설명하는 데 중점을 두고, 그 PMF를 직접 유도할 것이다. PMF의 유도과정에서 $e$가 왜 튀어나오는지, 팩토리얼은 왜 달려있는지 등을 자연스럽게 이해할 수 있을 것이다.
#1. 푸아송 분포의 정의
확률변수 $X$가 모수가 $\lambda$인 푸아송 분포(Poisson Distribution; 泊松分布)를 따를 때, $X \sim \mathrm{Pois}(\lambda)$라고 표현하고, $X$는 다음과 같은 PMF를 갖는다:
$$
f_{X}(x)=
\frac{e^{-\lambda}\lambda^{x}}{x!}
$$
푸아송 분포의 확률변수 $X$, 모수 $\lambda$는 다음과 같은 의미를 갖는다:
$\space$
$X$: 어떤 사건의 단위시간 또는 공간 내 발생횟수.
$\lambda$: 어떤 사건의 단위시간 또는 공간 내 평균 발생횟수.
#2. 확률변수 $X$, 모수 $\lambda$의 의미
푸아송 분포의 모수는 $\lambda$ 하나 뿐이다. 푸아송 분포는 이 $\lambda$를 이해하는 것이 관건이다. 다음과 같은 예제를 해결해보자.
“1시간에 평균 5대의 꼴로 버스가 지나간다는 사실을 알고 있다. 어느날 1시간에 버스가 3대 밖에 지나가지 않을 확률은 얼마일까?”
확률변수 $X$를 1시간안에 지나간 버스의 대수로 정의하면, $X\sim\mathrm{Pois}(5)$이고, PMF는 $f_{X}(x)=\frac{e^{-5}5^x}{x!}$이다. 그러므로 1시간안에 지나간 버스의 대수가 3일 확률은 $f_{X}(3)=\frac{e^{-5}\cdot5^3}{3!}$이다.
즉, 푸아송 분포는 ~시간안에 또는 ~공간안에 어떤 사건이 평균 $\lambda$회 발생한다는 사실을 이미 알고 있을 때, 그 사건이 실제로 $X$회 발생할 확률의 분포이다.
#3. 푸아송 분포의 PMF 유도
그런데 푸아송 분포의 PMF는 왜 이런 형태일까? 그 PMF를 직접 유도해보기로 하자. 먼저 이항분포에 대해 잘 알고 있어야 한다. 확률변수 $X$가 모수가 $(n,p)$인 이항분포(Binomial Distribution; 二项分布)를 따를 때, $X \sim \mathrm{Bin}(n,p)$라고 표현하고, $X$는 다음과 같은 PMF를 갖는다:
2022.10.06 - [확률론과 수리통계] - 이항분포
$$
f_{X}(x)={n \choose x}p^{x}(1-p)^{n-x}
$$
이항분포의 확률변수 $X$, 모수 $(n,p)$는 다음과 같은 의미를 갖는다:
$\space$
$X$: $n$번의 독립적인 베르누이 시행에서 성공 횟수.
$n$: 베르누이 시행의 횟수.
$p$: 각 베르누이 시행의 성공 확률.
$\space$
이항분포의 PMF에서 $p=\frac{\lambda}{n}$으로 놓고, $n \rightarrow \infty$을 가정하자. 이항분포의 PMF로부터 푸아송 분포의 PMF를 아래와 같이 유도할 수 있다.
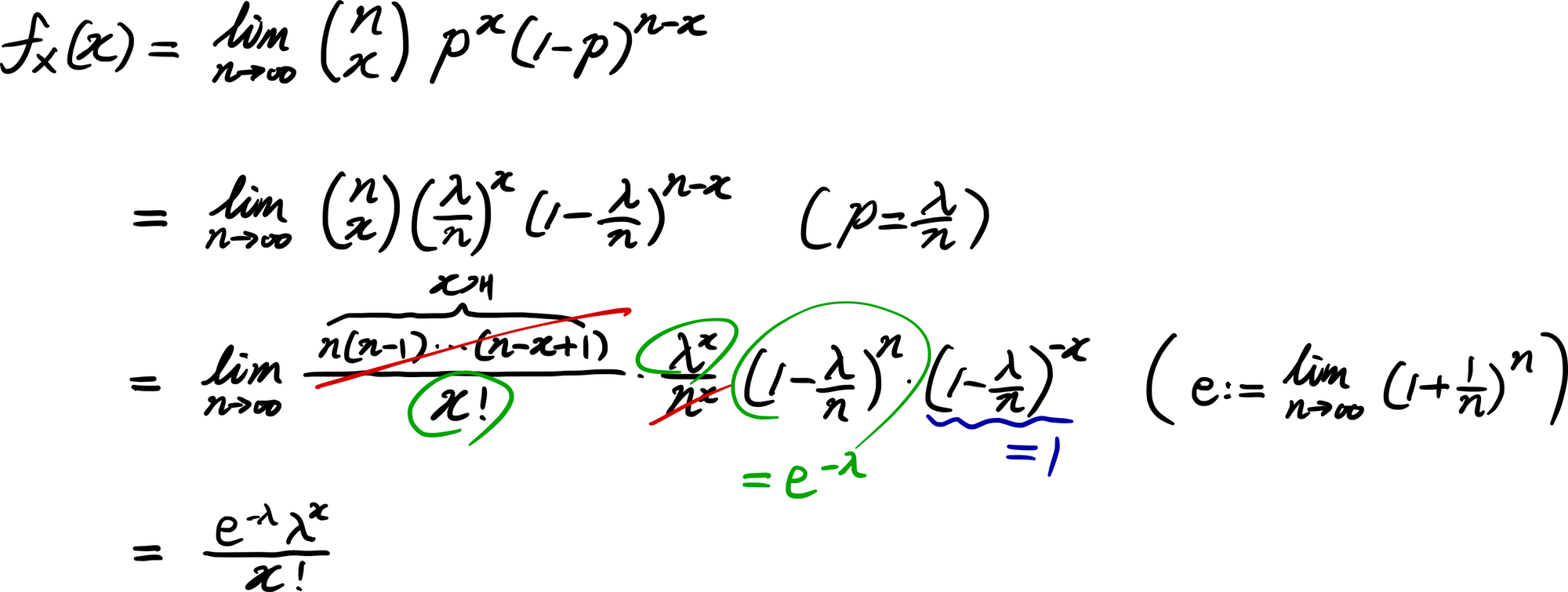
한편, $n \rightarrow \infty$이고 $\lambda$는 비교적 작은 상수이므로, 자연스럽게 $p \rightarrow 0$이다. 요약하자면, $\mathrm{Bin}(n,p)$은 $n \rightarrow \infty$, $p \rightarrow 0$일 때 $\mathrm{Pois}(np)$로 근사시킬 수 있다. 이처럼 $n \rightarrow \infty$일 때 두 분포가 같아지는 현상을 두고 분포수렴(Convergence in Distribution; 依分布收敛)이라고 한다. 즉, 푸아송 분포는 이항분포의 극한이라고 볼 수 있다.
#4. 푸아송 분포의 탄생계기
그런데 왜 이항분포를 극한으로 보내는 것을 생각해 냈을까? 큰 수를 다루는 이항분포의 확률을 직접 손으로 계산하려고 할 때 푸아송 분포가 유용함을 알 수 있다. 예를 들어 1%의 확률로 오판을 일으키는 AI판사가 1000 건의 사건을 심리했을 때, 오판인 사건이 5회를 넘어가는 확률을 계산해보자. 다음과 같이 식을 쓰는 것까지는 어렵지 않다. 여사건으로 접근하면 되기 때문이다.
$$
1-\sum_{k=0}^{5}{1000 \choose k}\left(0.01\right)^{k}\left(0.99\right)^{1000-k}
$$
이제 이것을 손으로 계산한다고 해보자. 시그마를 전개하면 분명 ${1000 \choose 5}$를 계산해야하는 순간이 온다. ${1000 \choose 5}=\frac{1000\cdot999\cdot998\cdot997\cdot996}{5!}$이므로 손으로 계산하기에는 매우 지저분한 숫자이다. AI판사가 1000 건이 아니라 10만 건을 심리한다면, 숫자는 더욱 지저분해진다. 심리 건수가 이보다 더 커지면 컴퓨터로도 계산할 수 없을지도 모른다.
푸아송 분포는 이런 계산을 수행할 때 도움이 된다. 이 예시는 이항분포에서 $n$이 매우 크고, $p$가 0에 가깝게 매우 작은 상황이라고 할 수 있다. 그러므로 이항분포에서 $n \rightarrow \infty$, $p \rightarrow 0$인 경우의 확률을 계산하는 것으로 볼 수 있다. 즉, 이항분포 $\mathrm{Bin}(1000,0.01)$을 푸아송 분포 $\mathrm{Pois}(10)$에 근사시키고, 다음과 같이 계산한다.
$$
\begin{split}
&1-\sum_{k=0}^{5}{1000 \choose k}\left(0.01\right)^{k}\left(0.99\right)^{1000-k}
\
&\approx1-\sum_{k=0}^{5}\frac{e^{-10}\cdot10^{k}}{k!}
\
&=1-e^{-10}\sum_{k=0}^{5}\frac{10^{k}}{k!}
\end{split}
$$
식이 여전히 복잡하지만, ${1000 \choose 5}=\frac{1000\cdot999\cdot998\cdot997\cdot996}{5!}$따위를 계산하는 것보다 $\frac{10^5}{5!}$의 계산이 편하다는 것은 자명하다.
note: 실제로 푸아송 분포는 프랑스 수학자 시메옹 드니 푸아송(Siméon Denis Poisson)이 민형사재판에서의 확률을 연구하면서 사용한 분포이다.
#5. 단위공간 또는 시간의 의미
푸아송 분포의 핵심 아이디어는 엄청나게 큰 $n$과 엄청나게 작은 $p$를 곱하면 서로 상쇄되어 적당한 수 $\lambda=np$가 나오는 것을 이용하는 것이다.이항분포가 엄청나게 큰 $n$을 갖는다는 것은 무슨 의미일까? 이항분포에서 $n$은 시행횟수이다. 그러므로 시행횟수가 매우 많은 상황을 뜻한다. 그렇다면 시행횟수가 매우 많은 상황은 어떤 상황일까?
흔히 낚시를 하는 상황으로 푸아송 분포를 설명하곤 한다. 강물에 낚시대를 드리우자. 그리고 시간을 잰다. 시간은 1초, 2초, …처럼 1초 간격으로 잴 수도 있지만 0.0001초, 0.0002초, …처럼 아주 작은 간격으로도 잴 수 있다. 강박증이 심한 어떤 사람 B씨가 이렇게 아주 작은 간격으로 시간을 재고, 매 간격초가 지날 때마다 물고기가 낚였는지 여부를 확인한다고하자. 이는 베르누이 시행이 아주 많은 것과 같다. 이런사람이 12567번째 시행, 즉 1.2567초가 지났을 때 물고기가 낚인 것을 확인할 확률은 0에 가깝다.
note: 푸아송(Poisson)은 프랑스어로 물고기라는 뜻이다.
그런데 강박증이 없는 사람 P씨는 보통 1시간 단위로 낚시를 즐긴다. 1시간 동안 낚시대를 드리우고, 옆의 친구와 잡담을 하거나 고민거리를 생각한다. 그리고 1시간안에 10마리 정도는 낚는다. 그런데 P씨에게 1시간, 즉 3600초라는 시간은 B씨에게 36000000회의 시행과 같다. B씨도 그 수많은 시행에서 10마리 정도의 물고기를 낚았을 것이다. 그럼 물고기를 낚을 확률은 얼마인가? B씨의 입장에서, 확률은 10/36000000으로 매우 작다. P씨의 입장에서도 확률은 똑같이10/36000000이지만, ‘1시간에 10마리의 물고기를 낚았으니 꽤 많이 낚았다’고 생각할 것이다.
똑같은 시간에 똑같은 마리 수의 물고기를 낚았지만, 두 사람의 기분에 차이가 생기는 이유는 사건을 보는 관점이 다르기 때문이다. P씨는 36000000회라는 수많은 베르누이 시행을 하나의 단위시간으로 보았기 때문에 여유를 가질 수 있었던 것이다. B씨는 그러지 않고 그 시행의 결과를 하나하나 따졌다. 바로 이것이 푸아송 분포와 이항분포의 차이이다. 1시간 동안 낚은 물고기의 마리 수를 확률변수 $X$로 놓았을 때, P씨와 B씨의 입장은 다음 두 분포로 요약할 수 있다.
$\space$
(1) P씨: $X\sim\mathrm{Pois}(10)$
(2) B씨: $X\sim\mathrm{Bin}(36000000, \frac{10}{36000000})$
$\space$
즉, 푸아송 분포는 이항분포에서 수많은 베르누이 시행을 묶어서 하나의 단위로 생각한다라고 이해하면 된다. 이 단위는 시간일 수도, 공간일 수도 있다. 한 페이지 당 오탈자가 평균 3개 발생한다고 알고 있을 때, 오탈자가 $X$개일 확률 같은 것은 ‘한 페이지’라는 공간을 단위로 한다.
note: $\lambda$를 어떤 사건의 단위시간 또는 공간 내 ‘평균’ 발생횟수라고 정의했다. 그런데 ‘평균’이라는게 정확히 무엇을 뜻할까? 실제로 푸아송 분포의 평균을 구해보면 $E(X)=\lambda$이다. 즉, 문자 그대로 평균 값이다. 그런데, 이항분포에서 $E(X)=np$이다. $\lambda=np$임을 감안할 때, 이것은 매우 재미있는 사실이다.



