분위수는 모수추정, 가설검정 등 각종 통계기법에 등장하므로 반드시 정리해두어야 한다. 당장 오늘 본 논문도 구간추정을 하는데 이 개념을 자연스럽게 쓰고 있었다.
#1. 정의
어떤 모집단의 확률분포 $F$(또는 확률변수 $X$)의 제$(1-\alpha)$ 분위수(Quantile; 分位数) $F_{\alpha}$는 다음 등식을 만족하는 모수다.
$$ F(F_{\alpha})=P(X\le F_{\alpha})=\int_{-\infty}^{F_{\alpha}}f(x)\space dx=1-\alpha $$
분위수를 누적분포함수의 역함수로 나타내기도 한다.
$$ F_\alpha:=F^{-1}(1-\alpha) $$
분위수는 수식보다 그림으로 접근하는 편이 이해가 쉽다.

쉽게 말해 어떤 데이터를 크기 순으로 나열했더니, 그 중 ‘어떤 수’보다 작거나 같은 값이 전체 데이터의 $(1-\alpha)$만큼, 보다 큰 값이 전체 데이터의 $\alpha$만큼 차지했다고 할 때, 이 ‘어떤 수’가 바로 제$(1-\alpha)$ 분위수가 된다.
만약 분포가 0을 기준으로 대칭이라면 $F_{1-\alpha}=-F_{\alpha}$가 성립한다.

분위수의 개념이 헷갈리는 것은 제$(1-\alpha)$ 분위수의 기호가 $F_{1-\alpha}$가 아니라 $F_{\alpha}$이기 때문이다. 하지만 그림과 기호만 기억하고 ‘제$(1-\alpha)$ 분위수’라는 개념은 머리속에서 삭제해버리면, 조금 덜 헷갈린다. 큰 쪽, 오른쪽만 신경쓰는 것이다. 마찬가지로 $F_{1-\alpha}$도 오른쪽에 $(1-\alpha)$만큼의 면적이 있다.
특히 자주 쓰이는 분위수의 표기를 알아두자. $F$가 해당하는 분포를 상징하는 문자로 대체된다. 뒤에 괄호가 붙기도 하는데, 괄호 안의 숫자는 분포의 모수(특히 자유도), 또는 베이즈 추정의 경우 관찰된 데이터, 조건 같은 것을 의미한다. z분포는 평균=0, 분산=1인 것을 굳이 표기할 필요가 없다.
$z_{\alpha}$: z분포
$\chi^2_{\alpha}(n)$: 자유도가 $n$인 카이제곱분포
$t_{\alpha}(n)$: 자유도가 $n$인 t분포
$F_{\alpha}(n,m)$: 자유도가 $n$, $m$인 F분포
#2. 백분위수, 사분위수, 5수요약
제$(1-\alpha)$ 분위수보다 작거나 같은 데이터가 ‘전체 데이터의 $1-\alpha$만큼 차지한다’는 것은 전체 데이터를 무한히 잘게 쪼개서 그중 $(1-\alpha)$만큼을 차지한다는 뜻이다.
그런데 실생활에서 쓰는 분위수는 데이터를 무한히 잘게 쪼개지 않고, 특정한 숫자로 쪼갠다. 대표적인것이 데이터를 100등분하는 백분위수(Percentile; 百分位数)와 데이터를 4등분하는 사분위수(Quartile; 四分位数)다.
백분위수는 특히 상대평가인 시험에서 성적을 산출할 때 많이 쓰는데, 어떤 사람의 시험성적 백분위가 99%=99/100라는 말은 그 사람보다 시험점수가 낮거나 같은 사람이 전체의 99%라는 말이며, 그 사람보다 시험을 잘 본 사람이 전체의 1% 밖에 안된다는 뜻이다. 이때, 이 사람의 시험점수는 제99 백분위수가 된다. 일반적으로 시험점수의 분포는 표준정규분포를 가정하므로 (보통 원점수를 표준점수로 환산해서 이렇게 되도록 만든다.) 시험점수는 $z_{0.01}$가 된다.
사분위수는 어떤 데이터의 대략적인 모습을 파악하는 데 쓰인다. 데이터를 크기 순으로 4등분하면, 총 5개의 숫자-최소값($\min$), 제1 사분위수($Q_1$), 중앙값($\mathrm{Med}$), 제3 사분위수($Q_3$), 최대값($\max$)이 나오는데, 이렇게 데이터를 4등분하는 5개의 숫자를 나타내는 것을 5수요약(Five-number Summary; 五数概括)라고 한다.
다음과 같은 상자그림(Box Plot; 箱线图)은 5수요약을 시각화하는데 적합한 그림이다.
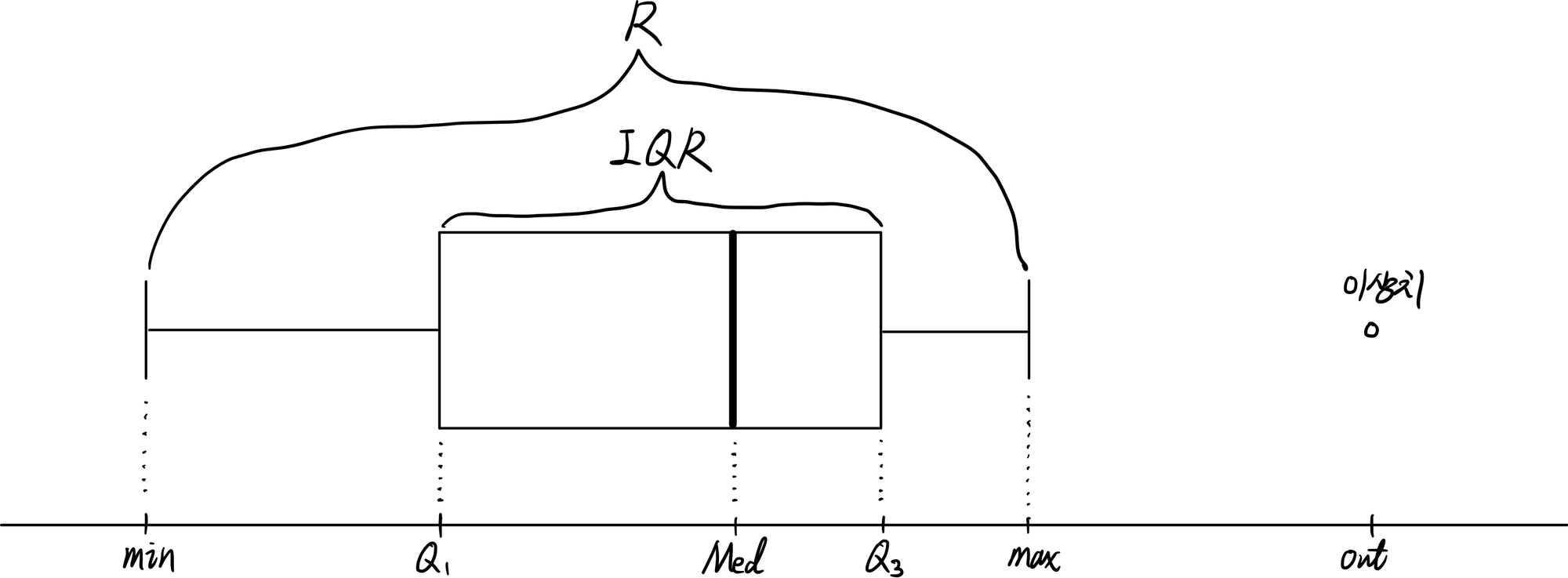
제1 사분위수와 제3 사분위수는 각각 Lower Quartile(下四分位数), Upper Quartile(上四分位数)라고도 한다. 이 두 숫자 사이의 거리를 사분위수 범위(Interquartile Range, IQR; 四分位距)라고 하며 $\mathrm{IQR}=Q_3-Q_1$로 계산한다. 데이터의 범위(Range, R; 全距)는 최대값과 최소값 사이의 거리인 $R=\max-\min$으로 계산한다.

