요약:

#1. t분포의 2가지 정의
$Z$ 통계량과 그것의 분포인 z분포는 유용하지만 단점이 하나 있는데, 바로 통계량에 모분산 $\sigma^2$이 들어가는 것이다. 실제 응용에서는 모분산을 알 수 없으므로, 이 모분산을 표본분산 $S^2$으로 대체한 $T$ 통계량과 t분포를 생각하게 된다.
(t분포의 1번째 정의) 다음과 같이 정의된 통계량 $T$의 분포를 자유도가 $(n-1)$인 t분포라고 하며, 기호로는 $t(n-1)$로 나타낸다.
$$ T:=\frac{\overline{X}-\mu}{S/\sqrt{n}}\sim t(n-1) $$
t분포의 자유도가 $(n-1)$인 이유는 표본분산의 자유도가 $(n-1)$이기 때문이다.
한편, $T$ 통계량은 다음과 같은 변형이 가능하다.
$$ T:=\frac{\overline{X}-\mu}{S/\sqrt{n}}={\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}}{\huge/}{\frac{\sqrt{\frac{(n-1)S^2}{\sigma^2}}}{\sqrt{n-1}}} $$
즉, 분자는 z분포를 따르는 확률변수로, 분모는 카이제곱분포를 따르는 확률변수의 변형으로 나타낼 수 있다. 물론 모집단은 정규분포를 따른다는 가정이 있어야 한다. 따라서 t분포를 다음과 같이 재정의할 수 있다.
(t분포의 2번째 정의) 통계량 $Z\sim\mathrm{N}(0,1)$, $\chi^2\sim\chi^2(n-1)$이며, $Z\perp\chi^2$일 때, 다음과 같이 정의된 통계량 $T$의 분포를 자유도가 $(n-1)$인 t분포라고 한다.
$$ T:=\frac{Z}{\sqrt{\chi^2/(n-1)}}\sim t(n-1) $$
그런데 매번 $(n-1)$로 쓰기 귀찮으니까 이걸 $v$로 바꿔서 간단히한다.
$$ T:=\frac{Z}{\sqrt{\chi^2/v}}\sim t(v) $$
주의점: $(n-1)$을 $n$으로 바꿔서 다음과 같이 표기하는 경우도 흔하다. 이때 $n$과 $(n-1)$에서 $n$이 갖는 의미는 다르므로 주의할 것. 아래의 식에서 $n$은 표본의 크기가 아니라 자유도를 나타내는 하나의 부호라고 이해하면 편하다.
$$ T:=\frac{Z}{\sqrt{\chi^2/n}}\sim t(n) $$
만약 t분포의 자유도를 $n$이라고 놓았다면, 표본의 크기는 $(n+1)$임을 염두에 두자.
#2. t분포의 확률밀도
t분포의 1번째 정의는 탄생계기, 목적에 가깝고, 2번째 정의는 확률밀도를 구하는데 이용된다.
지난 글에서 확률변수의 변환과 사칙연산의 분포를 다뤘다. 이 내용을 t분포의 확률밀도를 유도하는 데 써먹을 것이다.
유도의 로직: 분모의 분포를 2단계에 걸쳐서 구하고, 마지막으로 분자에서 분모를 나눈 것의 분포를 구해서 총 3단계에 걸쳐서 유도한다.
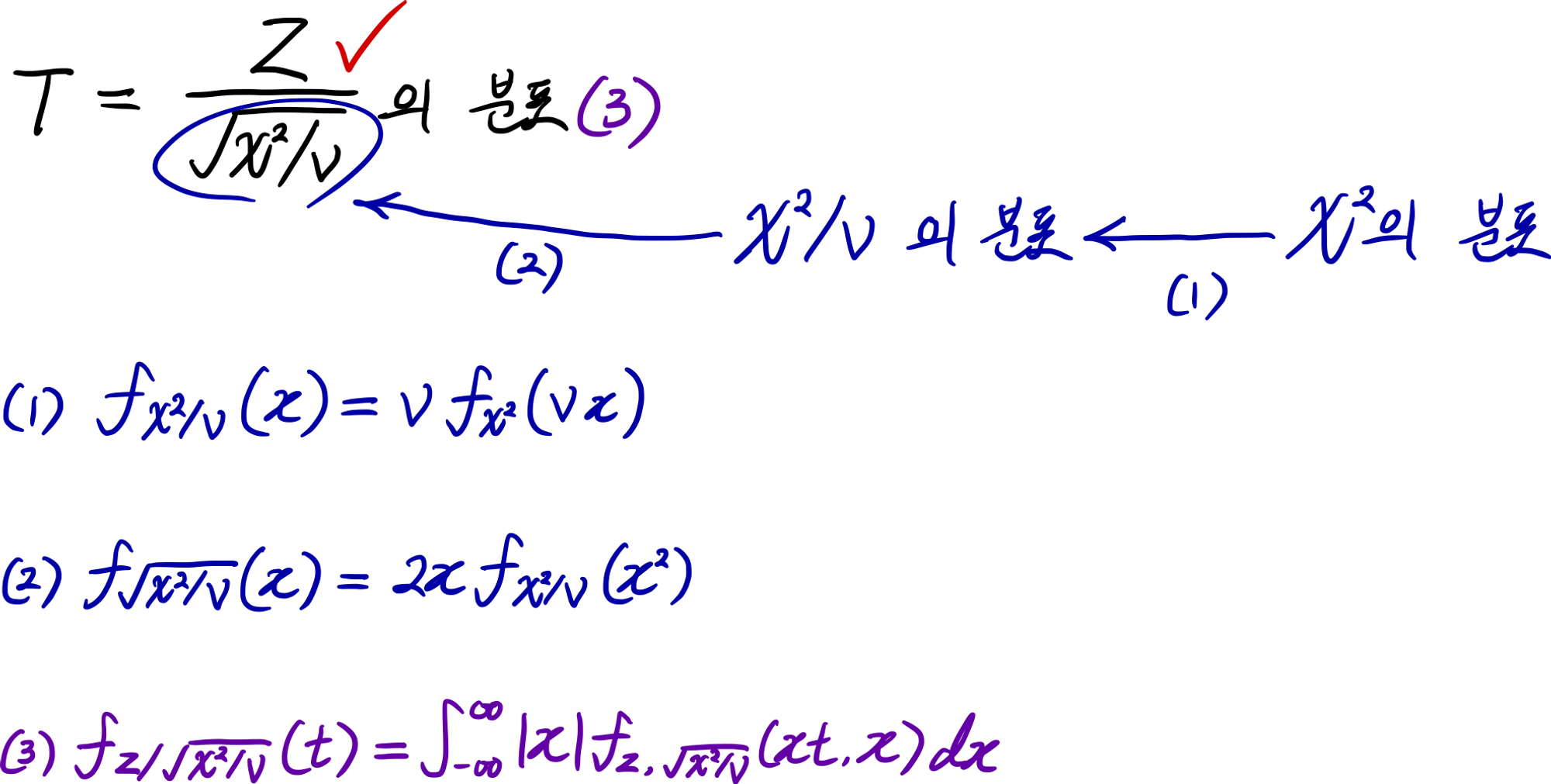
계산과정: $u$의 거듭제곱과 $e^{-u}$를 곱한 것의 적분을 감마함수로 나타낼 수 있음을 생각하면서 그런 형태가 되도록 적절히 치환해야 됨. $Z$ 통계량과 $\chi^2$ 통계량이 서로 독립인 점도 이용해야 함. (‘표본분산의 분포’의 이해와 증명 참조.) 지시함수는 적분구간을 전체 실수구간에서 양의 실수구간으로 바꾸는 역할을 한다.

결과물: $t(v)$의 확률밀도는 다음과 같다.
$$ f_{T}(t)=\frac{\Gamma(\frac{v+1}{2})}{\sqrt{v\pi}\Gamma(\frac{v}{2})}\left(1+\frac{t^2}{v}\right)^{-\frac{v+1}{2}} $$
#3. t분포의 성질
(1) 자유도가 $v$인 t분포의 $n\to\infty$일 때의 극한은 z분포다.
$$ \lim_{v\to\infty}t(v)=\mathrm{N}(0,1) $$
t분포는 z분포의 대체품이므로, 두 분포 사이의 관계는 매우 중요하다.
증명: 먼저 t분포의 정규화상수 $\frac{\Gamma[(v+1)/2]}{\sqrt{v\pi}\Gamma(v/2)}$는 무시하고, 뒤의 $t$에 관한 항 $\left(1+\frac{t^2}{v}\right)^{-\frac{v+1}{2}}$을 보자. 딱봐도 $v\to\infty$일 때 $e$와 관련있게 생겼다. 실제로 계산을 해보면
$$ \begin{split} \lim_{v\to\infty}\left(1+\frac{t^2}{v}\right)^{-\frac{v+1}{2}}&=\lim_{v\to\infty}\left[\left(1+\frac{1}{v/t^2}\right)^{v/t^2}\right]^{-t^2/2}\left(1+\frac{t^2}{v}\right)^{-1/2} \\ &=e^{-t^2/2} \end{split} $$
이므로, $\lim_{v\to\infty}f_{T}(t)=Ce^{-t^2/2}$이다. 여기서 $C$는 새로운 정규화 상수가 될 것이고, 그 값은 다음과 같다.
$$ C=\frac{1}{\int_{-\infty}^{\infty}e^{-t^2/2}\space dt}=\frac{1}{\sqrt{2\pi}} $$
따라서 t분포의 자유도 $v$가 충분히 크면 z분포에 수렴한다. 자유도 $v=n-1$을 늘리는 방법은 표본의 크기 $n$을 키우는 것으로, 표본을 많이 뽑아야한다고 강조하는 이유다.
(2) t분포는 좌우대칭이다.
z분포와 마찬가지로 $t_{1-\alpha}=-t_{\alpha}$가 성립한다.
#4. t분포와 중심극한정리, 큰 수의 법칙
흔히 “표본의 크기가 충분히 크다면 모집단의 분포와 상관없이 t분포를 사용가능하며, 반면 표본의 크기가 작을 때 t분포를 사용하기 위해서는 모집단이 정규분포를 따른다는 가정이 들어가야 한다.”고 한다. 정말 그런지 CLT와 LLN을 이용해서 확인해보자.
#4.1 모집단이 정규분포일 때
우선 모집단이 정규분포 $\mathrm{N}(\mu,\sigma^2)$를 따른다고 가정해보자. 그러면 $T$ 통계량은 다음과 같이 변형이 가능하다.
$$ T:=\frac{\overline{X}-\mu}{S/\sqrt{n}}={\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}}{\huge/}{\frac{\sqrt{\frac{(n-1)S^2}{\sigma^2}}}{\sqrt{n-1}}} $$
분자를 보면, 모집단이 정규분포를 따르기 때문에 그것의 선형변환인 $Z:=\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}$은 당연히 정규분포를 따른다. 그런데 하필이면 이 선형변환은 표준화 변환이므로 변환 후의 평균과 분산은 각각 0과 1이 된다. 따라서 $Z:=\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim\mathrm{N}(0,1)$이다.
분모를 보면, 모집단이 정규분포이므로 $\frac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1)$이다.
t분포의 2번째 정의에 의해, $T$ 통계량은 $t(n-1)$을 따른다. 여태까지의 논의에서 표본의 크기 $n$은 어떤 역할도 하지 않는다. 따라서 모집단이 정규분포를 따를 때, 표본의 크기와 상관 없이 $T$ 통계량은 $t(n-1)$을 따른다.
#4.2 모집단이 정규분포가 아닐 때
모집단이 정규분포가 아닌 다른 분포라고 가정해보자. 이번에도 $T$ 통계량의 정의는 같고, 이 통계량이 과연 t분포를 따르는지가 중요하다. 이번에는 다음과 같이 변형해보자.
$$ T:=\frac{\overline{X}-\mu}{S/\sqrt{n}}={\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}}{\huge/}{\frac{S}{\sigma}} $$
분자를 보면, 표본의 크기 $n\to\infty$일 때, $Z:=\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}$는 모집단의 분포가 무엇이든 상관없이 표준정규분포를 따른다. 중심극한정리의 핵심내용이다.
분모를 보면, 표본의 크기 $n\to\infty$일 때, 표본분산 $S^2$은 모분산 $\sigma^2$에 a.s. 수렴한다. 큰 수의 법칙의 핵심내용이다. (표본평균과 표본분산의 극한 참조.) 따라서 분모는 1에 a.s. 수렴한다.
이상을 종합하면, 모집단이 정규분포가 아닐 경우 $T$ 통계량은 표준정규분포를 따르는 확률변수에 a.s. 수렴하는데, 위에서 표준정규분포는 t분포의 극한임을 밝혔다.
결론적으로 표본의 크기가 충분히 크다면 $T$ 통계량은 모집단의 분포와 상관없이 t분포를 따른다고 볼 수 있다.
'확률론과 수리통계' 카테고리의 다른 글
| 적률 추정법 (0) | 2023.02.21 |
|---|---|
| 표본평균과 표본분산의 극한 (0) | 2023.02.16 |
| ‘표본분산의 분포’의 이해와 증명 (0) | 2023.02.12 |
| 자유도 (0) | 2023.02.12 |
| 카이제곱분포 (0) | 2023.02.12 |
