# $\alpha$오류, $\beta$오류
지금까지 했던 논의를 되돌아보면, 통계적 가설검정법은 제1종 오류의 발생률인 유의확률(=p값) $p$와 제1종 오류의 발생률의 상한선인 유의수준 $\alpha$의 비교가 핵심이다. 구체적인 p값과 유의수준을 비교하거나, 우회적으로 관측값과 임계값을 비교하는 방법을 쓰거나, 결국 핵심은 제1종 오류, 즉, 옳은 영가설을 기각할 오류의 발생률을 줄이는 것이다.
‘옳은 영가설을 기각’한다는 것은, 다시 말해 ‘실제로 없는 차이를 있다’고 하는 것이다. 그런데 실제 응용측면에서는 ‘틀린 영가설을 채택’할 오류, 즉, ‘실제 있는 차이를 없다’고 하는 오류도 신경써야 한다. 이것을 제2종 오류라고 한다.
제2종 오류는 제1종 오류와 달리 유의확률이나 유의수준 같은 개념이 없다. 그만큼 가설검정에서는 상대적으로 경시되는 개념인 것이다. 하지만 실전에서는 분명히 제1, 2종 오류를 동시에 신경써야 하는 상황이 온다.
두 오류를 함께 논의하는 경우, 제1종 오류의 발생률을 $\alpha$로 놓고, 제2종 오류의 발생률을 이것에 대응해서 $\beta$로 놓는다. 제1종 오류와 제2종 오류를 간단히 $\alpha$오류와 $\beta$오류라고 한다.

# 두 가지 오류의 trade-off 관계
$\alpha$나 $\beta$나 작을 수록 좋다. 그런데 늘 그렇듯 두 마리 토끼를 다 잡을 수는 없다. MMSE 문제에서 편향과 분산이 trade-off 관계에 있었듯이, $\alpha$와 $\beta$도 trade-off 관계에 있다.
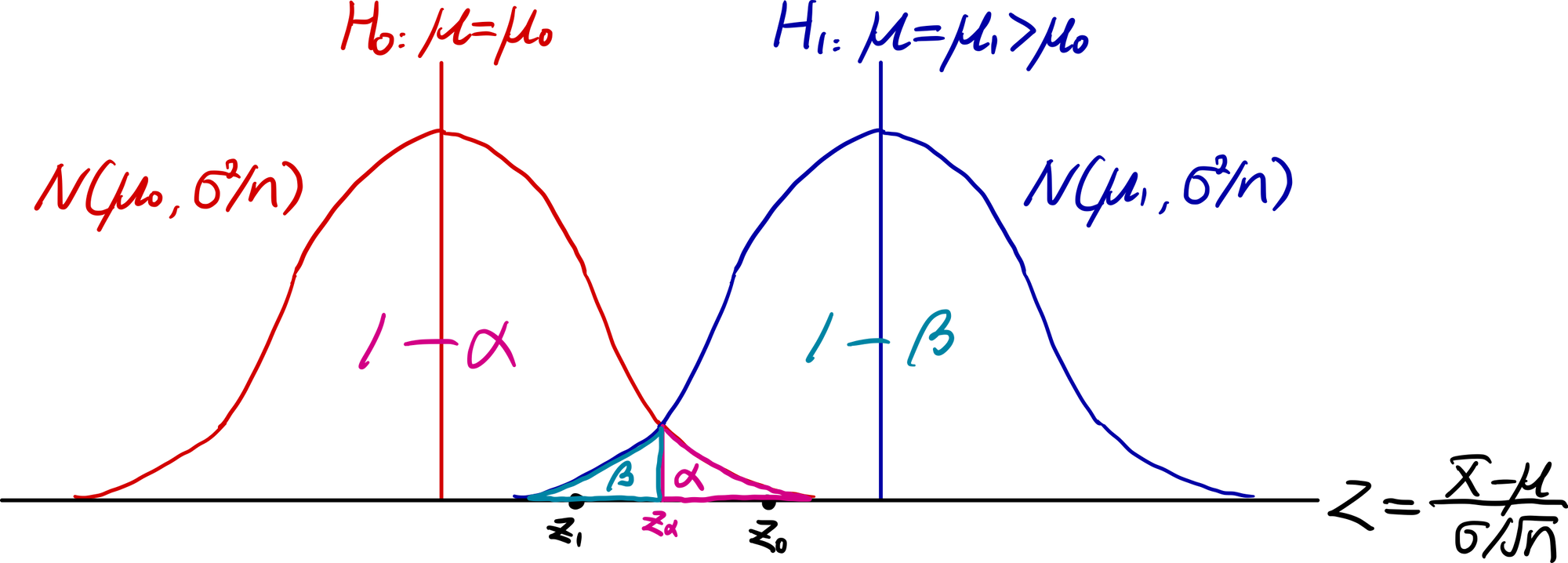
단일표본 우측 z검정을 예시로 생각해보자. 유의수준 $\alpha$에 영가설 $H_0:\mu=\mu_0$과 대립가설 $H_1:\mu>\mu_0$을 제안할 것이다. 그리고 $H_0$이 옳다는 가정하에 적당한 검정통계량 $Z:=\frac{\bar X-\mu_0}{\sigma/\sqrt{n}}$의 확률분포를 그래프로 나타낸다. 검정통계량의 임계값은 $z_\alpha$가 된다.
데이터를 얻어 검정통계량의 관측값 $z$를 계산한 뒤, 임계값 $z_\alpha$와 비교한다. $z<z_\alpha$이면 기각역 밖에 있으므로 $H_0$을 채택하고, $z>z_\alpha$이면 기각역에 속하므로 $H_0$을 기각한다. 그림처럼 점 $z_0$에서 영가설 채택이, 점 $z_1$에서 영가설 기각이 발생한다.

상술한 과정이 바로 제1종 오류만 신경썼던 전통적인 z검정이다. 이제 제2종 오류를 고려해보자. 위의 빨간색 분포는 $H_0$을 기반으로 만든 분포인데, 사실 원래 얻어야할 실제 분포는 파란색이었다고 ‘가정’하자. 파란색 분포는 빨간색 분포와 평균만 다를 뿐, 분산은 같다.
파란색 분포는 대립가설 $H_1:\mu>\mu_0$에 기반한 분포다. $H_0$이 틀렸다는 가정 하에 $\mu>\mu_0$이므로 $\mu$의 실제 값은 $\mu_0$이 아닌 $\mu_1$로 놓자.

이렇게 실제 분포(가정)와 영가설의 분포를 나란히 놓고 영가설 채택점 $z_0$을 보자. 실제 분포가 옳다는 가정하에, $z_0$은 제2종 오류를 범한 것이 된다. 실제 분포가 옳다는 가정하에 $H_0$은 틀렸고, $z_0$은 틀린 $H_0$을 채택하는 것이 되기 때문이다.
note: $H_0$의 기반한 분포든 실제 분포든 모두 하나의 가정일 뿐이다. 실제로 평균이 $\mu_0$인지 $\mu_1$인지는 알 수 없다.
반면, 실제 분포가 옳다는 가정하에, $z_1$은 옳은 판단이 된다. 실제 분포가 옳다는 가정하에 $H_0$은 틀렸고, $z_1$은 틀린 $H_0$을 기각했기 때문이다. 이 논리를 그대로 따르면 실제 분포(가정)의 확률밀도함수를 $(-\infty,z_{\alpha})$ 구간에서 적분한 값이 $\beta$가 되며, $(z_{\alpha},\infty)$ 구간에서 적분한 값이 $1-\beta$가 된다.
만약 $\beta$를 줄이고 싶다면, 임계값 $z_\alpha$를 왼쪽으로 이동시켜야만 한다. 이 과정에서 필연적으로 $\alpha$가 증가한다. 반대로, $\alpha$를 줄이고 싶어서 임계값 $z_\alpha$를 오른쪽으로 이동시키면 $\beta$는 증가한다.

그래프 아래 면적을 통해 논의하지 않고, 직관적으로 생각해보자. $H_0:무죄$, $H_1:유죄$와 같이 프로그래밍 된 AI 판사가 있다. AI 판사가 범죄자를 놓치기 싫어서 유죄판결 성향이 강한 경우, 실제로 유죄일 때 무죄판결을 할 확률($\beta$)은 감소한다. 범죄자를 놓칠 확률은 감소하는 것이다. 하지만 이와 반대급부로 실제로 무죄일 때 유죄판결을 할 확률($\alpha$)은 증가한다. 동시에 억울한 사람이 생길 확률도 증가하는 것이다. 반면, 무죄판결 성향이 강한 경우 억울한 사람이 생길 확률($\alpha$)은 감소하지만 범죄자를 놓칠 확률($\beta$)이 증가한다.
note: 범죄자를 놓치는 것(제2종 오류, $\beta$오류)보다 억울한 사람이 생기는 것(제1종 오류, $\alpha$오류)이 더 심각하므로 ‘무죄추정의 원칙’에 의해 무죄판결 성향이 더 강하도록 프로그래밍 하는 것이 옳다고 본다.
$\alpha$와 $\beta$는 trade-off 관계에 있지만, $\alpha+\beta$를 최소화하는 것은 가능하다. 다음 그림처럼 $\alpha=\beta$가 되도록 임계값을 설정하면, $\alpha+\beta$가 최소화된다. 위 그림과 비교해서 ‘위에 튀어나온 면적’이 없어졌기 때문이다.
'확률론과 수리통계' 카테고리의 다른 글
| 혼동행렬, 신호탐지이론, ROC 곡선 (0) | 2023.03.14 |
|---|---|
| 검정력, 적당한 표본의 크기 (0) | 2023.03.13 |
| 단일표본, 독립표본, 대응표본 t검정 (0) | 2023.03.12 |
| t검정과 p값에 대해 (2) | 2023.03.11 |
| 두 정규분포 모집단의 가설검정 (0) | 2023.03.10 |

