# 크라메르-라오 하한
지난 글에서 모평균의 MVUE를 얻기 위해 라그랑주 승수법을 이용했다. 이번에는 다른 방식으로 접근해보자.
임의의 모수 $\theta$의 불편추정량 $\hat{\theta}$의 분산의 하한을 생각해보자. 이 하한은 크라메르-라오 하한(Cramér-Rao Lower Bound, CRLB; 克拉默-拉奥下界)이라고 부르며, 모든 불편추정량의 분산의 ‘이론상 하한’이다.
note: ‘이론상 하한’이라는 말은 불편추정량의 분산이 이 하한값을 가지지 못할 수도 있음을 뜻한다. $a\ge0$일 때, $a=0$이라고 단언할 수 없는 것과 마찬가지다. 따라서 크라메르-라오 하한은 MVUE를 얻기 위한 한 방법일 뿐, 실제로 MVUE의 분산이 크라메르-라오 하한이라고 단정할 수 없다.
불편추정량의 CRLB는 로그 가능도를 추정하려는 모수로 편미분한 것의 역수와 같다. 즉, 다음 부등식이 모든 불편추정량 $\hat{\theta}$에 대해 성립한다.
$$ \mathrm{Var}[\hat{\theta}]\ge(\mathrm{Var}[\frac{\partial\ln L}{\partial\theta}])^{-1} $$
증명: $\frac{\partial L}{\partial\theta}=L\frac{\partial\ln L}{\partial\theta}$를 잘 이용하는 것이 중요하다. PDF를 전체 구간에서 적분하면 1인 것도 이용했다. 피적분 함수를 두 함수의 곱으로 쪼갠 후 코시-슈바르츠 부등식을 적용하는 아이디어를 기억해야겠다.
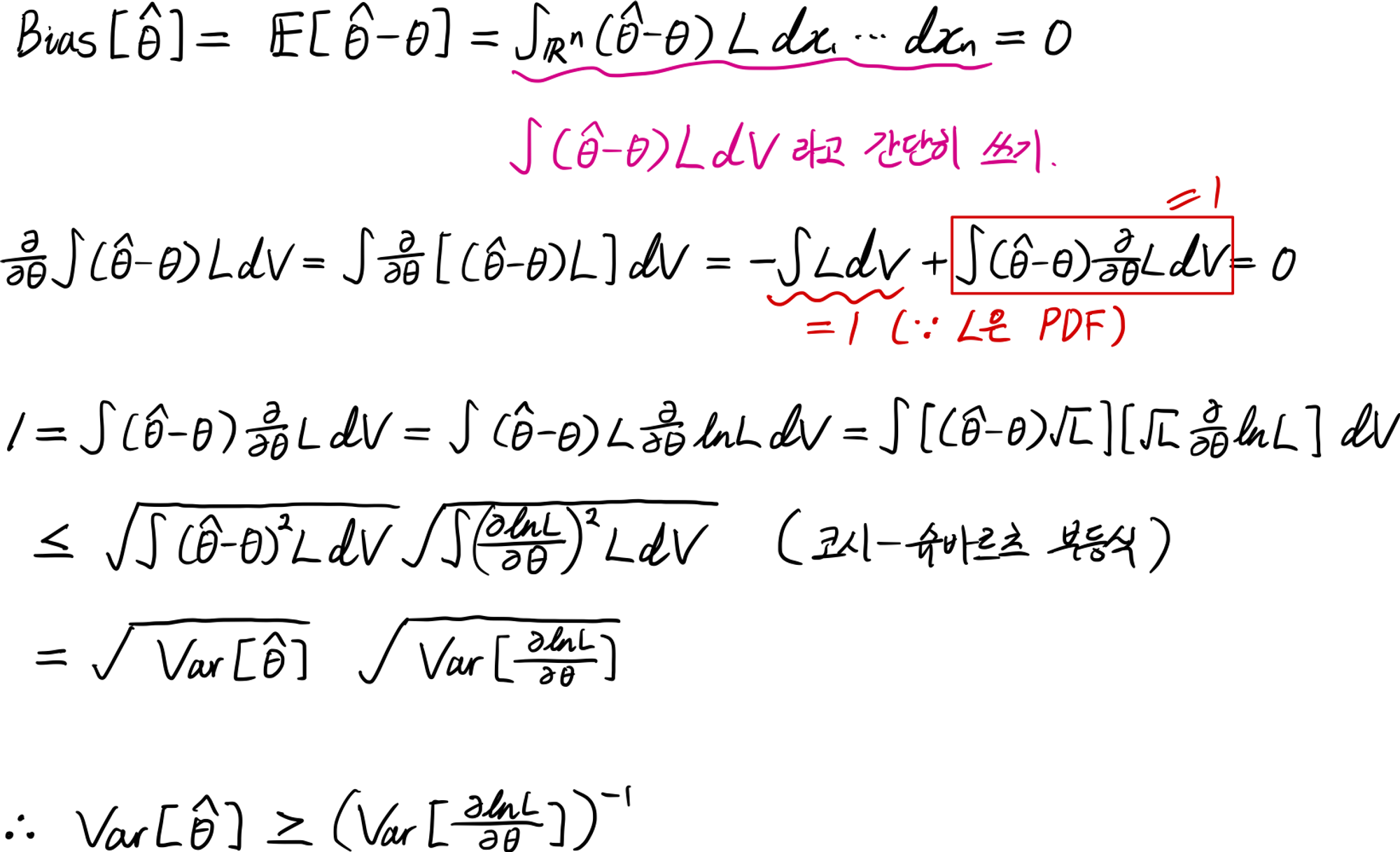
식에서 $\mathrm{Var}[\frac{\partial\ln L}{\partial\theta}]$는 피셔 정보(Fisher Information, FI; 费希尔信息)라고 한다. 즉, 크라메르-라오 하한은 피셔정보의 역수이다.
$$ \mathrm{CRLB}=\mathrm{FI}^{-1} $$
# 피셔 정보 계산 공식
피셔 정보를 계산하는 공식은 다음과 같다.
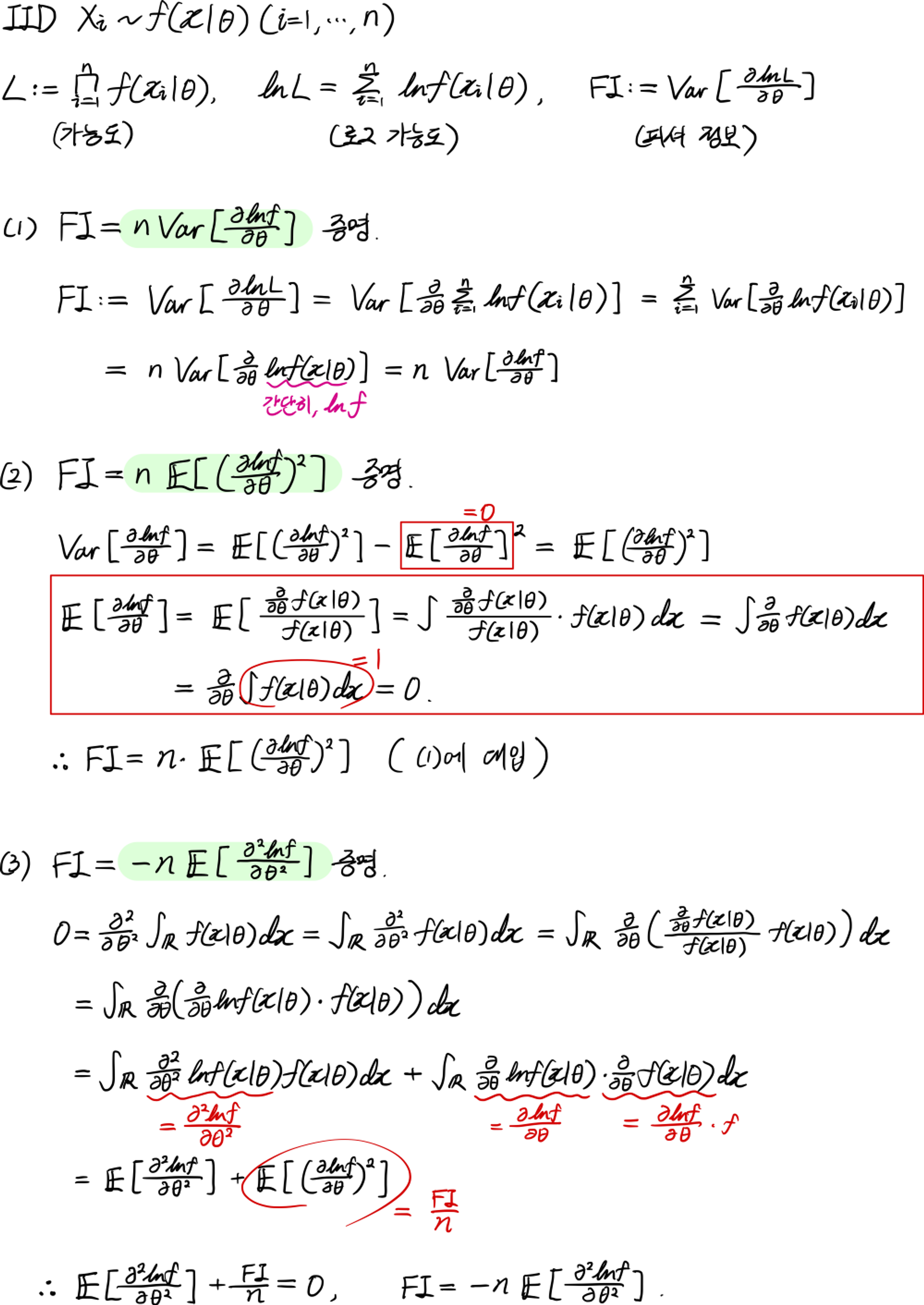
$$ \mathrm{FI}:=\mathrm{Var}[\frac{\partial\ln L}{\partial\theta}]=n\mathbb{E}[(\frac{\partial\ln f}{\partial\theta})^2]=-n[\frac{\partial^2\ln f}{\partial\theta^2}] $$
증명: 이번에도 $\frac{1}{f}\frac{\partial f}{\partial\theta}=\frac{\partial\ln f}{\partial\theta}$처럼 로그의 미분을 이용하는 것이 중요했고, PDF의 전체 구간 적분 값이 상수 1이라는 것을 충분히 이용하는 것이 중요했다.
# 피셔 정보의 의미
피셔 정보는 어떤 의미를 가지고 있는지 알아보기 위해, 3번째 공식을 변형해보자.
$$ \mathrm{FI}=-n\mathbb{E}[\frac{\partial^2\ln f}{\partial\theta^2}]=\mathbb{E}[-\frac{\partial^2\ln f^n}{\partial\theta^2}]=\mathbb{E}[-\frac{\partial^2\ln L}{\partial\theta^2}] $$
즉, 피셔 정보는 $-\frac{\partial^2\ln L}{\partial\theta^2}$의 기댓값이며, 로그 가능도의 이계도함수와 관련이 있다.
로그 가능도는 일반적으로 아래로 오목한 모양이므로, 이계도함수는 음수의 값을 가진다. 따라서 $-\frac{\partial^2\ln L}{\partial\theta^2}=\vert\frac{\partial^2\ln L}{\partial\theta^2}\vert$는 이계도함수의 절대적 크기다.
MLE의 목적은 로그 가능도를 최대화 하는 $\theta$를 찾는 것이다. 로그 가능도가 최대화되는 곳 근처에서 이계도함수의 절대적 크기가 매우 크다고 가정해보자. 이는 접선의 기울기가 매우 빠르게 변한다는 뜻으로, 함수의 그래프의 곡률이 매우 클 것이다. 따라서 로그 가능도 곡선은 매우 뾰족한 모양일 것이다.
로그 가능도는 확률밀도함수이기도 하다. 그래프가 ‘뾰족한 모양’이라는 것은 특정 지점에서 확률밀도가 높고, 집중되어 있다는 것을 의미한다. 그렇다면 찾으려는 $\theta$는 그 부근에 존재할 것이라고 쉽게 판단할 수 있다. 반면 그래프가 평평한 모양이라면, 로그 가능도를 최대화 하는 $\theta$를 쉽게 찾을 수 없다. 모든 지점의 확률밀도가 고만고만하기 때문이다.
지난 글에서 베타분포가 베이즈 추정에 응용되는 것을 논의했다. 이것을 발판삼아 이해해보자. 승률이라는 모수에 대해 아무런 정보가 없는 상태에서, 무정보 사전분포로 $\mathrm{Beta}(1,1)$을 가정해보면, 그래프는 평평한 수평선이다. 따라서 승률이 어떤가에 대해서 쉽게 논의할 수 없다.
여기에 많은 정보를 업데이트 해서 얻은 $\mathrm{Beta}(1579, 2098)$와 같이 큰 모수의 베타분포의 그래프는 특정 지점에서 뾰족한 모양이었다. 이때는 충분한 정보가 있으므로 자신있게 승률에 대해서 논의할 수 있다. 정보를 더 많이 업데이트 할 수록, 그래프는 점점 더 뾰족해질 것이다.

note1: 물론 베이즈 추정은 가능도가 아닌 사후확률 $f(\theta\mid X)$을 최대화 하는 방법이다. 가능도 $f(X\mid\theta)$를 최대화 하는 것과는 다르다. 하지만, 그래프가 뾰족할 때 모수에 대해 많은 정보를 가지고 있다는 사실은 같다.
note2: 베이즈 추정은 모수에 대한 지식인 사전분포를 활용하는 추정이다. 반면 최대가능도 추정은 모수에 대한 사전분포의 개입이 없다. 그런데 흔히 사전분포를 무정보 사전분포인 $\mathrm{Beta}(1,1)=\mathrm{U}[0,1]$로 놓는데, 이러면 사전분포를 활용하지 않은 것이나 마찬가지이므로 베이즈 추정이나 최대가능도 추정이나 같은 방법이라고 볼 수 있다.
따라서 로그 가능도 곡선의 뾰족한 정도로 모수에 대한 정보량을 나타내는 것은 합리적인 생각이다. 이것이 바로 크라메르-라오 하한을 떠나, 피셔 정보의 진정한 의미라고 생각한다.
'Mathematics' 카테고리의 다른 글
| 구간추정 (0) | 2023.03.03 |
|---|---|
| 베셀 보정, 표본분산의 분모 (0) | 2023.03.02 |
| 최소분산 불편추정량 (2) | 2023.02.27 |
| 추정량의 불편성, 효율성, 일치성 (0) | 2023.02.23 |
| 최대가능도 추정법 (0) | 2023.02.21 |


