확률공간의 3요소인 표본공간, 보렐필드, 확률측도를 모두 정의했다. 보렐필드의 원소를 사건이라고 하고, 확률측도는 줄여서 확률이라고 했다. 그리고 확률의 공리와 그로부터 따라나오는 여러가지 성질도 탐구했다.
이 정도면 확률론을 기술할 기본적인 준비는 갖춘 셈이다. 그럼 제일 간단한 확률모델인 ‘동전 던지기’를 분석해보자. 우리는 동전을 던져서 앞면이 나올 확률이 1/2, 뒷면이 나올 확률이 1/2임을 알고있다. 이것이 왜 성립하는지 확률론적으로 설명해보자.
‘동전 던지기’라는 확률시행의 결과는 앞면($H$) 또는 뒷면($T$)이다. 확률시행의 결과, 사건, 표본공간, 보렐 필드를 다음과 같이 나타내자.
$\space$
(1) 결과: $\omega=H$ 또는 $\omega=T$
(2) 표본공간: $\Omega=\lbrace H,T \rbrace$
(3) 사건: $\emptyset$, $\lbrace H \rbrace$, $\lbrace T \rbrace$, $\Omega$
(4) 보렐 필드: $\mathcal{F}=\lbrace \emptyset, \lbrace H \rbrace, \lbrace T \rbrace, \Omega \rbrace$
$\space$
확률의 공리 (2), (3)에 의해, 다음이 성립한다.
$$
1=P(\Omega)=P(\lbrace H\rbrace\cup\lbrace T\rbrace)=P(\lbrace H\rbrace)+P(\lbrace T\rbrace)
$$
그런데 동전이 공평하다는 전제하에, 두 근원사건인 $\lbrace H\rbrace$와 $\lbrace T\rbrace$의 확률이 같다. 즉, $P(\lbrace H\rbrace)=P(\lbrace T\rbrace)$이다. 따라서 다음이 성립한다.
$$
\begin{cases}
P(\lbrace H\rbrace)+P(\lbrace T\rbrace)=1
\
P(\lbrace H\rbrace)=P(\lbrace T\rbrace)
\end{cases}
\Rightarrow
\begin{cases}
P(\lbrace H\rbrace)=\frac{1}{2}
\
P(\lbrace T\rbrace)=\frac{1}{2}
\end{cases}
$$
즉, 동전 던지기의 각 사건의 확률이 1/2인 이유는, 확률의 공리 (2), (3), 그리고 두 근원사건인 ‘앞면이 나온다’와 ‘뒷면이 나온다’의 확률이 같기 때문이다. 확률의 공리는 어디서나 성립하는 기본적인 가정이므로, 사실상 핵심원인은 두 근원사건의 확률이 같다는 데 있다.
만약 표본공간을 구성하는 사건이 동전 던지기처럼 2개가 아니라 $n$개라면, 각 근원사건의 확률은 $1/n$으로 같을 것이다. 이렇게 근원사건의 개수가 유한개이면서 각 근원사건의 확률이 서로 같은 확률모델을 고전적 확률(Classical Probability; 古典概型)이라고 한다. 고전적 확률은 다음과 같이 계산한다.
$$
P(E)=\frac{\lvert E \rvert}{\lvert \Omega \rvert}
$$
예를 들어, 빨간색 공이 8개, 파란색 공이 2개 들어있는 상자에서, 파란색 공을 뽑는 사건을 $E$라고 하면, $P(E)=2/10=0.2$이다. ($\lvert \Omega \rvert=8+2=10$)
고전적 확률모형은 단순하지만 그만큼 응용의 소지가 많다. 이 글에서는 확률론에서 자주 언급되는 2가지 모형에 대해 알아보자.
#1. 폴리아 항아리
지난 글에서 복원추출과 비복원추출에 의거한 분포인 이항분포와 초기하분포를 설명했다. 고전적 확률모형에서 가장 유명한 것이 바로 복원추출 모형과 비복원추출 모형이다. 사실 이 두 가지의 모형은 폴리아 항아리 (Pólya Urn; 波利亚罐子) 모형에 포함된다. 폴리아 항아리 모형은 다음과 같은 상황을 가정한다:
“빨간공 $a$ 개와 파란공 $b$ 개가 들어있는 항아리에서 공 1 개를 무작위로 꺼낸다. 공의 색을 확인한 뒤, 꺼낸 공과 같은 색의 공 $c$ 개를 항아리에 넣는다.”
즉, 복원추출은 $c=1$인 상황을, 비복원추출은 $c=0$인 상황을 가정한 것이다. 그리고 $c>1$이라면 공의 개수가 많아질 것이다. 폴리아 항아리는 아주 간단한 모형이지만, 디리클레-다항분포(Dirichlet-Multinomial Distribution; 狄利克雷多项分布)라는 머신러닝에서 아주 중요한 확률분포를 이해하는 데 핵심인 모델이다.
#2. 상자에 공 넣기
다음과 같은 ‘상자에 공 넣기(Balls into Boxes; 投球入盒)’ 문제도 고전적 확률에서 자주 다루는 소재이다:
“$n$개의 공을 $m(>n)$개의 상자에 모두 넣으려고 한다. 상자에는 1번부터 $m$번까지의 번호가 붙어있다. 이때, 1번부터 $n$번까지의 상자에 공이 1개씩만 들어있을 확률 $P(E)$를 구하여라.”
이 문제는 간단해보이지만, $n$개의 공이 서로 구분 가능한가(Distinguishable; 可辨)의 여부와 상자가 여러개의 공을 담을 수 있는지 여부로 답이 갈린다. (상자는 번호가 붙어있으므로 구분가능하다고 본다.) 이 문제의 대표적인 3가지 풀이를 정리하면 다음과 같다.
$\space$
(1) 맥스웰-볼츠만(Maxwell-Boltzmann, MB; 麦克斯韦-玻尔兹曼) 통계
공이 구분가능하며, 상자의 용량이 무제한이라고 가정하자.
$\lvert \Omega \rvert$를 구하자. 임의의 공 1개는 1번부터 $m$번까지의 상자에 들어갈 수 있다. 즉, $m$가지의 경우가 있다. 그리고 상자의 용량이 무제한이므로 모든 공에 대해 $m$가지의 경우가 있다. 그런데 이런 공이 총 $n$개가 있다고 했다. 그러므로 $\lvert \Omega \rvert=m^n$이다.
$\lvert E \rvert$를 구하자. 공이 구분가능하므로 순서대로 $b_1$, $b_2$, $\cdots$, $b_n$과 같이 이름을 붙여주자. 그리고 상자도 구분이 가능하므로 순서대로 $B_1$, $B_2$, $\cdots$, $B_m$과 같이 이름을 붙여주자. 1번부터 $n$번까지의 상자에 공이 1개씩 들어가는 사건에 대해 생각해야 한다. $n=3$이라고 해보자. 이 경우 가능한 사건 중 하나는 $b_1$-$B_1$, $b_2$-$B_2$, $b_3$-$B_3$과 같이 매칭되고, 나머지 $m-3$개의 상자는 비어있는 것이다. 물론 $b_2$-$B_1$, $b_3$-$B_2$, $b_1$-$B_3$과 같이 매칭될 수도 있다. 결국 모든 가능한 경우의 수는 $b_1$, $b_2$, $b_3$을 순서대로 나열하는 것과 같으므로 $3!$이다. 이것을 임의의 $n$으로 일반화 하면 $\lvert E \rvert=n!$이다.
이상을 종합하면, $P(E)=\frac{n!}{m^n}$이다.
$\space$
(2) 페르미-디랙(Fermi-Dirac, FD; 费米-狄拉克) 통계
공의 구분이 불가능하며, 각 상자에 최대 1개의 공만 넣을 수 있다고 가정하자.
$\lvert \Omega \rvert$를 구하자. 임의의 공 1개는 1번부터 $m$번까지의 상자에 들어갈 수 있다. 즉, $m$가지의 경우가 있다. 그런데 상자의 용량이 최대 1개 이므로 임의의 공 1개가 어떤 상자에 들어갔다고 가정했을때, 2번째의 공은 $(m-1)$개의 상자라는 선택지 밖에 없다. 이런 식으로 $n$개의 공을 모두 넣을 때까지 진행하면 경우의 수는 다음과 같다.
$$
m(m-1)(m-2)\cdots\left(m-(n-1)\right)=\frac{m!}{(m-n)!}
$$
그리고 공의 구분이 불가능하므로 $n$개의 공의 배열 순서는 의미가 없다. 따라서 이 값에서 $n!$을 나눈 값이 최종적인 경우의 수이다. 즉, $\lvert \Omega \rvert=\frac{m!}{(m-n)!n!}={m \choose n}$이다.
$\lvert E \rvert$를 구하자. (1)에서 처럼 공과 상자에 이름을 붙여주자. 경우의 수는 $n!$이다. 그런데 공의 구분이 불가능하므로 $n$개의 공의 배열 순서는 의미가 없다. 따라서 이 값에서 $n!$을 나눠주면 $\lvert E \rvert=\frac{n!}{n!}=1$이다.
이상을 종합하면, $P(E)=\frac{1}{{m \choose n}}$이다.
$\space$
(3) 보스-아인슈타인(Bose-Einstein, BE; 玻色-爱因斯坦) 통계
공의 구분이 불가능하며, 상자의 용량이 무제한이라고 가정하자.
우선 (2)와 같이, $\lvert E \rvert=\frac{n!}{n!}=1$이다. 공의 구분이 불가능하기 때문이다.
결국 핵심은 $\lvert \Omega \rvert$를 구하는 것이다. 공 $n=3$개와 상자 $m=5$개를 가정해보자. 그리고 사건의 결과를 $\boldsymbol{\omega}=(\omega_1,\omega_2,\omega_3,\omega_4,\omega_5)$와 같이 나타내자. 이 중, $\omega_i$는 $i$번째 상자에 담긴 공의 개수이다. 예를 들어, 상자의 용량이 무제한이므로 공 3개가 첫번째 상자에 전부 들어갈 수 있고 나머지는 전부 비어있는 사건이 있을 수 있다. 이것을 $\boldsymbol{\omega}=(3,0,0,0,0)$이라고 하자. 또 다른 경우로, 첫번째 상자에 공 2개, 세번째에 공 1개가 들어갈 수도 있다. 이것을 $\boldsymbol{\omega}=(2,0,1,0,0)$처럼 나타내자. 이런 방식으로 경우의 수를 따져야 한다.
이럴 때 좋은 방법은 ‘칸막이’를 이용하는 것이다. 상자가 5개 있으므로 칸막이는 총 4개 필요하다. 직선을 5토막 내는 데 4개의 칼질이 필요한 것과 같은 이치이다. 그림처럼 직선을 5개의 공간으로 분할하고, 그 직선을 향해서 3개의 공이 떨어지는 것을 상상해보자.

모든 공이 직선 위에 떨어진 후, 다음 그림처럼 공과 칸막이의 일직선 상의 배열이 나타날 것이다. 결국 3개의 공과 4개의 칸막이를 일직선 상에 배열하는 경우의 수를 구해야 한다. 그러므로 $\lvert \Omega \rvert={7\choose 3}$이다.
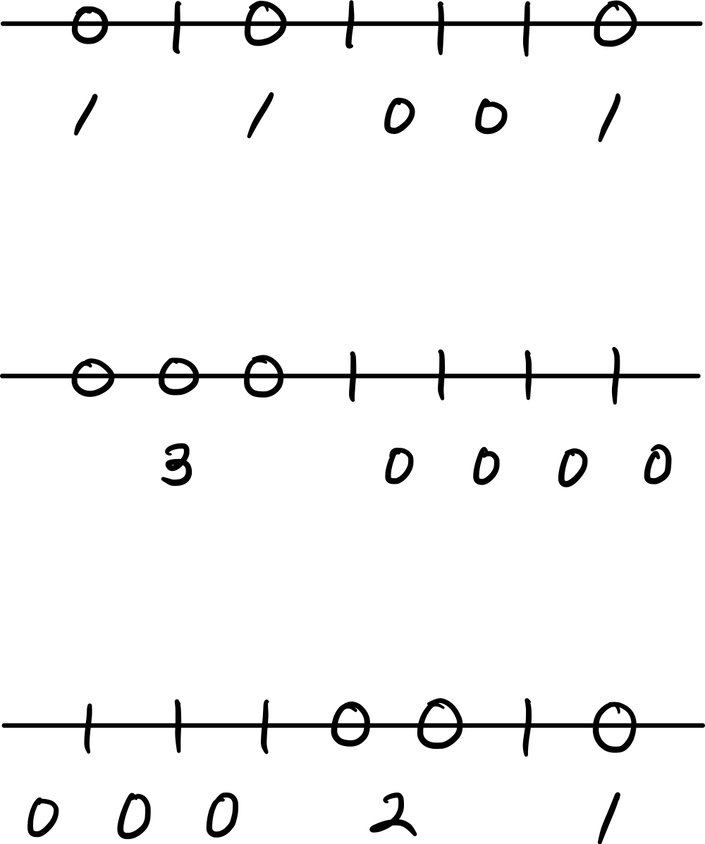
이제 이것을 일반화 하면 $n$개의 공과 $(m-1)$개의 칸막이를 일직선 상에 배열하는 경우의 수이다. 따라서 $\lvert \Omega \rvert={n+m-1\choose n}$이다.
이상을 종합하면 $P(E)=\frac{1}{{n+m-1 \choose n}}$이다.
$\space$
상자에 공 넣기 문제는 통계역학에서 응용된다. 이 문제에서 공을 입자, 상자를 입자의 양자상태(State; 量子态)라고 놓는 것이다. FD통계를 따르는 입자를 페르미온(Fermion; 费米子), BE통계를 따르는 입자를 보손(Boson; 玻色子)이라고 한다. 그리고 상자의 용량이 무제한인가, 즉 하나의 상태에 여러 입자가 들어갈 수 있는지 여부는 파울리 배타원리(Pauli Exclusion Principle; 泡利不相容原理)에 대응된다. 페르미온은 하나의 상태에 하나의 입자만 들어갈 수 있으므로 파울리 배타원리를 따른다. 보손은 배타원리를 따르지 않는다.


