기본사건이 유한개이면서 각 기본사건의 확률이 같은 확률모형을 고전적 확률모형이라고 했다. 이번에는 기본사건이 비가산무한개이면서 각 기본사건의 확률이 같은 확률모형인 기하학적 확률(Geometric Probability; 几何概型)을 알아보자.
#1. 두 사람의 만남
기하학적 확률모형을 배울 때 꼭 나오는 예시가 다음과 같은 ‘두 사람의 만남’문제이다.
“두 사람이 저녁 7시~8시에 공원에서 만나기로 했다. 먼저 공원에 도착한 사람은 아직 도착하지 않은 사람을 20분 동안 기다린 후 공원을 떠난다. 두 사람이 만날 확률 $P(E)$를 구하여라.”
$\space$
풀이: 두 사람이 공원에 도착했을 때의 시각을 저녁 7시+$x$분, 저녁 7시+$y$분이라고 하자. 저녁 7시부터 8시까지 만나기로 했으므로
$$
\Omega=\lbrace(x,y):0<x<60,0<y<60\rbrace
$$
두 사람은 모두 공원에 도착한 후 20분만 기다린다. 따라서 두 사람의 도착시각의 차이는 20분 이하여야 한다.
$$
E=\lbrace(x,y)\in\Omega:\lvert x-y \rvert\le20\rbrace
$$
$\Omega$, $E$를 그림으로 나타내면 다음과 같다. 면적의 비를 통해 계산하면 $P(E)=\frac{\lvert E \rvert}{\lvert \Omega \rvert}=\frac{5}{9}$이다.

#2. 르베그 측도
‘두 사람의 만남’문제와 같이 기하학적 확률모형에서는 이렇게 도형의 면적을 통해 사건의 확률을 계산한다. 면적 외에도, 길이, 부피도 이용된다. 정확히는 $n$차원 유클리드 공간 $\mathbb{R}^n$에서 르베그 측도(Lebesgue Measure; 勒贝格测度)를 계산하는 것이다.
가측공간 $(\mathbb{R},\mathcal{F})$ 위의 측도 $\lambda$가 다음을 만족하면 $\lambda$를 르베그 측도라고 한다. 여기서 $\mathcal{F}$는 보렐 필드이다.
$$
\lambda(\lbrack a,b\rbrack)=b-a
$$
르베그 측도는 쉽게 말해 도형의 길이, 넓이(길이$\times$길이), 부피(길이$\times$길이$\times$길이)같은 것을 수학적으로 엄밀하게 정의한 것이며, 집합 $S$의 르베그 측도는 $\lambda(S)$와 같이 나타낸다. 다시 말해 위의 예시에서 $\vert E\vert=\lambda(E)$인 것이다.
르베그 측도에 대해 깊게 파고들지 않아도, 다음과 같은 중요한 사실 몇가지는 기억해 둘 필요가 있다.
$\space$
(1) 보렐 측도와 르베그 측도의 관계
르베그 측도를 사용하여 측정하려면 르베그 가측이어야 한다. 그런데 보렐 가측이면 르베그 가측이다. 즉, 보렐-시그마 대수 $\mathcal{B}$와 르베그-시그마 대수 $\mathcal{L}$에 대해, $\mathcal{B} \subset \mathcal{L}$이다. 확률론은 보렐 필드에서 전개되므로 걱정할 필요가 없다. 하지만 르베그 가측이면서 보렐 가측이 아닌 집합, $\mathcal{L}-\mathcal{B}$도 존재하는데, 유명한 예시가 칸토어 집합(Cantor Set; 康托集)이다.
(2) 영집합과 완비화
보렐-시그마 대수는 모든 열린 집합에 의해 생성된 시그마대수이고, 르베그-시그마 대수는 모든 열린 집합과 영집합(Null Set; 零测集)에 의해 생성된 시그마대수이다. 따라서 르베그-시그마 대수가 보렐 필드를 포함하는 것이다. 영집합은 길이($\mathbb{R}$ 위의 외측도를 의미한다. 후술.)가 0인 집합으로, $\mathbb{R}$에서 $\lbrace 1\rbrace$, $\lbrace1\rbrace\cup\lbrace2\rbrace$같은 것이다. 르베그 측도는 모든 열린 집합은 물론 영집합까지 측정할 수 있으므로 보렐 측도의 완비화(Completion; 完备化)라고 여겨진다.
(3) 영집합과 공집합
영집합은 공집합(Empty Set; 空集)과는 다르다. 공집합은 발생이 아예 불가능한 집합이고 영집합은 발생이 가능하다. $\lbrace 1 \rbrace$은 분명히 표본점 1을 포함하고 있다. 그런데 공집합 $\lbrace\rbrace$은 어떤 표본점도 가지고 있지 않다. 예를 들어 $\lbrack0,1\rbrack$에서 임의의 점 $x$를 고를 때, $x=0.5$일 확률은 0이다. 확률은 0이지만 사건 $\lbrace 0.5 \rbrace$는 분명히 일어난다. $x=1.5$일 확률도 0이다. 이 경우는 발생이 불가능하다. 다시 말해 확률이 0이라는 것은 불가능사건의 필요조건이고, 충분조건이 아니다. 영집합과 공집합 모두 확률측도가 0이어서 혼동하기 쉽다.
(4) 외측도
다음과 같은 두가지 경우를 생각해보자.
표본공간이 $\Omega=[0,10]$이면 $\lambda(\Omega)=10$이다. 사건 $E=[0,1]$이면 $\lambda(E)=1$이다. 따라서 $P(E)=1/10$이다. 이 확률은 선분에서 선분 하나를 골라내는 확률이다.
이번에는 $\Omega^2=[0,10]\times[0,10]$을 생각해보자, 이 경우는 $\lambda(\Omega^2)=100$이다. 여기서도 사건 $E=[0,1]$이고, $\lambda(E)=1$이다. 그러면 $P(E)=1/100$이라고 할 수 있을까? 이 확률은 직사각형 구간에서 선분 하나를 골라내는 확률로, 0이어야 한다. 직사각형은 비가산무한개의 선분으로 이루어져 있기 때문이다. 따라서 $1/100$이라고 할 수 없을 것이다.
르베그 측도를 믿고 사용했더니 이와 같은 모순이 생겼다. 이것을 설명하기 위해서 외측도(Outer Measure; 外测度)라는 개념을 도입하자.
첫번째 경우, $E=\lbrace x\in\mathbb{R}:0\le x\le1\rbrace$이고 이것의 르베그 외측도 $\lambda^{\ast}(E)=1$이다. 따라서 $\lambda^{\ast}(\Omega)=10$인 경우, $P(E)=1/10$이다.
두번째 경우, $E=\lbrace(x,0)\in\mathbb{R^2}:0\le x\le 1\rbrace$의 르베그 외측도 $\lambda^{\ast}(E)=0$이다. 따라서 $\lambda^{\ast}(\Omega)$와 무관하게 $P(E)=0$이다.
즉, $\mathbb{R}$에서의 외측도인가, $\mathbb{R}^2$에서의 외측도인가에 따라 답이 갈리는 것이다. $\mathbb{R}$에서의 외측도를 길이(Length; 长度)라고하고, $\mathbb{R}^2$에서의 외측도를 넓이(Area; 面积)라고 하자. 위와 같은 결과는 ‘선분의 길이는 1이지만 넓이는 0이다’라는 것을 수학적으로 표현한 것이다. 물론 $\mathbb{R}^3$에서의 외측도는 부피(Volume; 体积)이고, 선분의 부피는 0이므로 $E=\lbrace(x,0,0)\in\mathbb{R^3}:0\le x\le 1\rbrace$에 대해서도 $\lambda^{\ast}(E)=0$일 것이다.
#3. 뷔퐁의 바늘실험
이제 기하학적 확률과 르베그 측도에 대해 어느정도 감이 잡혔으니, 또 다른 유명한 예시인 뷔퐁(Buffon)의 바늘실험에 대해 알아보자.
“평면 위에 간격이 $a$인 평행선이 여러 개 있다. 높은 곳에서 길이가 $l$인 바늘을 떨어뜨리자. 이 바늘이 평행선과 교차할 확률 $P(E)$를 구하여라.”
바늘의 중심의 평행선까지의 거리를 $x$로 두고, 바늘이 평행선과 이루는 각을 $\theta$로 놓으면, 바늘이 평행선과 교차한다는 사건은 $E=\left\lbrace(\theta,x)\in\Omega:x\le \frac{l}{2}\sin\theta\right\rbrace$같이 나타낼 수 있다. (그림 참조.) 여기서 $\Omega=\left\lbrace(\theta,x):0\le\theta\le\pi,0\le x\le\frac{a}{2}\right\rbrace$이다. (위쪽 평행선만 고려하기 때문이다.)

집합 $\Omega$와 $E$를 $\mathbb{R}^2$에서 나타내면 다음 그림과 같다.

따라서 다음과 같이 계산할 수 있다.
$$
P(E)=\frac{\int_{0}^{\pi}\frac{l}{2}\sin\theta\space\mathrm{d}\theta}{\frac{a}{2}\pi}=\frac{2l}{a\pi}
$$
계산결과에 원주율이 포함된다. 따라서 이 식을 변형하여 원주율의 근사치를 구할 수 있다.
$$
\pi=\frac{2l}{aP(E)}\approx\frac{2l}{a\cdot\frac{n}{N}}
$$
$N$은 바늘을 떨어뜨린 횟수, $n$은 바늘이 평행선과 교차한 횟수이다. 시행횟수 $N$이 충분히 클 때 수학적 확률이 통계적 빈도와 같아지는 것을 이용한다. 실제로 많은 수학자들이 바늘을 몇 천번씩 떨어뜨려 원주율의 근사치를 구해냈다.
#4. 베르트랑의 역설
기하학적 확률에서 또 다른 유명한 예시인 베르트랑(Bertrand)의 역설은 확률론에서 흔히 사용되는 무작위(Random; 随机)라는 용어를 사용하는 데 경각심을 준다. 베르트랑의 역설은 다음과 같은 문제를 제기한다.
“임의의 원에서 현을 무작위로 하나 골랐을 때, 그 현의 길이가 원에 내접하는 정삼각형의 한 변의 길이보다 클 확률 $P(E)$를 구하여라.”
이 문제의 답은 다음과 같은 3가지이다.
$\space$
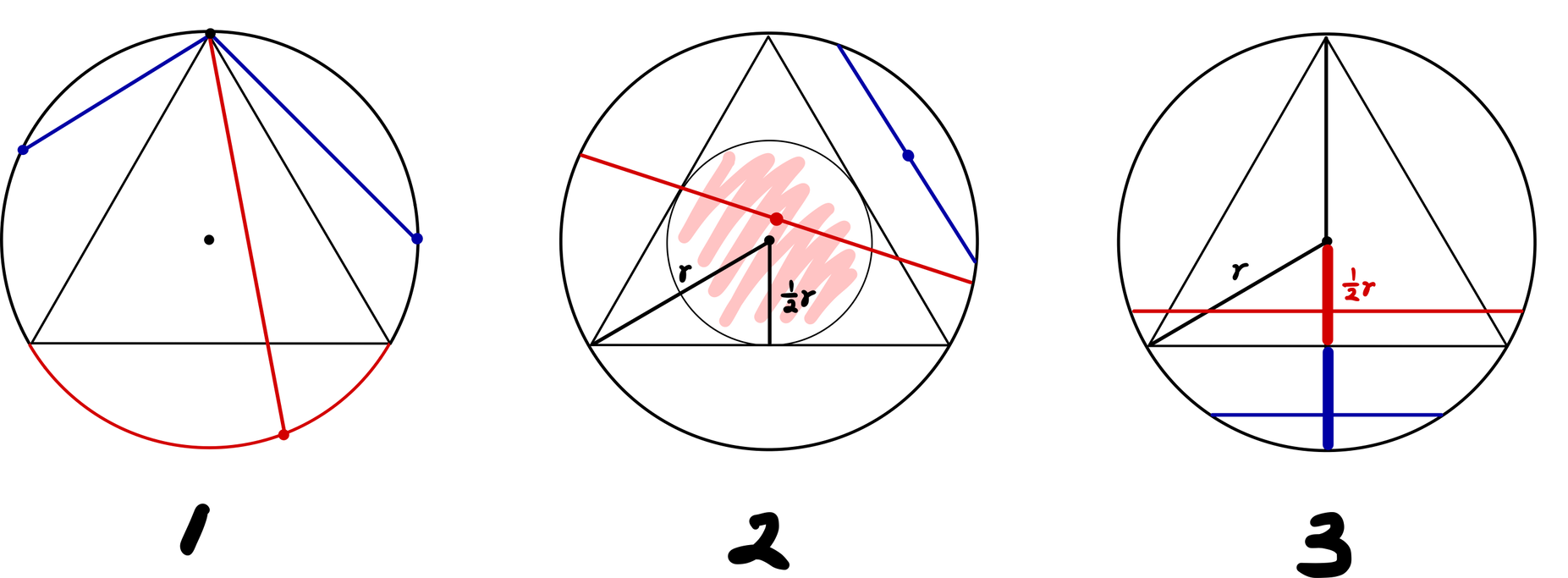
(1) 무작위 끝점(Random Endpoint)
현의 시작점을 원내접 정삼각형의 한 꼭지점으로 삼자. 그리고 현의 끝점을 원 위에서 무작위로 선택하자. 그림1과 같이, 현이 원내접 정삼각형의 한 변의 길이보다 크려면 현의 끝점이 현의 시작점과 마주보는 호 위에 있어야 한다. 이러한 호는 원주의 1/3을 차지하므로 $P(E)=1/3$이다.
(2) 무작위 중점(Random Midpoint)
임의의 현은 그 중점에 의해서 유일하게 결정된다. 원의 반지름을 $r$로 두면, 원내접 정삼각형에 내접하는 작은 동심원의 반지름은 $\frac{1}{2}r$이다. 현의 중점이 바로 이 작은 동심원 내부에 있으면 조건을 만족한다(그림2). 이 작은 동심원과 원의 반지름비는 $1/2$이므로, 면적비는 $1/4$이다. 따라서 $P(E)=1/4$이다.
(3) 무작위 거리(Random Distance)
현은 임의의 지름과 수직하는 선분이다. 따라서 현과 원심과의 거리 $d$에 따라서 현의 길이가 결정된다. 원의 반지름을 $r$이라고 하면 $0\le d\le r$이다. $d$는 이 범위 내에서 무작위의 값을 가질 것이다. 그림3과 같이 , $d$가 $r/2$보다 작을 때 현의 길이가 원내접 정삼각형의 한 변보다 크다. 따라서 $P(E)=\frac{r/2}{r}=1/2$이다.
$\space$
같은 문제인데 3가지 모순되는 답이 나오는 이유는 ‘무작위’라는 말의 모호함에 있다. 어떤 것을 무작위로 할 것인가에 따라 다른 것이다.



