이번 글에서는 가장 간단한 연속분포인 균등분포를 설명하겠다.
확률변수 $X$가 모수가 $(a,b)$인 균등분포(Uniform Distribution; 均匀分布)를 따를 때, $X \sim \mathrm{U}(a,b)$라고 표현하고, $X$는 다음과 같은 PDF를 갖는다:
$$
f_
{X}(x)=\frac{\mathbf{1}_
{\lbrack a,b \rbrack}(x)}{b-a}
$$
균등분포의 확률변수 $X$, 모수 $(a,b)$는 다음과 같은 의미를 갖는다:
$\space$
$X$: 구간 $\lbrack a,b \rbrack$에서만 관측값을 가지며, 그 구간내의 모든 점의 근처의 값을 가질 확률이 동일한 변수.
$a$: 구간의 시작점.
$b$: 구간의 끝점.
$\space$
정의가 복잡한 듯 보이지만, 쉽게 말해 $X$가 어떤 구간내의 값을 랜덤으로 가지면 $X$가 균등분포를 따른다고 생각할 수 있다. 여기서 랜덤이라는 것은 각각의 관측값에 대한 확률밀도가 같다는 것이다. 실제로 균등분포의 PDF는 $x \in [a,b]$일 때 상수 $\frac{1}{b-a}$이다. 또, $X$가 구간 $\lbrack a,b \rbrack$에서만 관측값을 가져야 하므로, 지시함수 $\mathbf{1}_{\lbrack a,b\rbrack} (x)$을 곱해서 $x \notin [a,b]$일 때 PDF를 0으로 만들어야 한다.
그런데 왜 상수가 $\frac{1}{b-a}$일까? 우선 $(b-a)$는 구간 $[a,b]$의 길이이다. 즉, $X$의 확률밀도는 (1/구간의 길이)라는 것으로, 구간을 균등하게 나눈 것 중 한 조각이라고 볼 수 있다.
상수가 $\frac{1}{b-a}$인 또 다른 이유가 있다. 균등분포의 PDF를 다음과 같이 2부분으로 분해해보자.
$$
f_
{X}(x)
=\frac{\mathbf{1}_
{\lbrack a,b \rbrack}(x)}{b-a}
=\frac{1}{b-a}\cdot{\mathbf{1}_
{\lbrack a,b \rbrack}(x)}
$$
여기서 앞의 상수가 $\frac{1}{b-a}$이 아닌 임의의 상수 $C$라면 어떨까? 즉, 다음과 같이 나타내자.
$$
f_
{X}(x)
=C \cdot \mathbf{1}_
{\lbrack a,b\rbrack} (x)
$$
$f_{X}(x)$가 PDF가 되려면 $\int_{-\infty}^{\infty}f_{X}(x)\space\mathrm{d}x=1$을 만족해야 한다. 즉 다음이 성립해야 한다.
$$
C \cdot \int_
{-\infty}^{\infty} \mathbf{1}_
{\lbrack a,b\rbrack} (x) \space \mathrm{d}x=1
$$
여기서 지시함수의 적분을 계산해야 한다. $\mathbf{1}_
{\lbrack a,b\rbrack} (x)
:=
\begin{cases}
1, & x \in \lbrack a,b\rbrack
\\
0, & x \notin \lbrack a,b\rbrack
\end{cases}$이므로 적분구간을 적절히 나누어 계산하자.
$$
\begin{split}
\int_
{-\infty}^{\infty} \mathbf{1}_
{\lbrack a,b\rbrack}(x) \space \mathrm{d}x
&=\int_
{-\infty}^{a}\mathbf{1}_
{\lbrack a,b\rbrack}(x) \space \mathrm{d}x
+\int_
{a}^{b}\mathbf{1}_
{\lbrack a,b\rbrack}(x) \space \mathrm{d}x
+\int_
{b}^{\infty}\mathbf{1}_
{\lbrack a,b\rbrack}(x) \space \mathrm{d}x
\\
&=0+(b-a)+0
\\
&=b-a
\end{split}
$$
위와 같이, $\int_
{-\infty}^{\infty} \mathbf{1}_
{\lbrack a,b\rbrack}(x) \space \mathrm{d}x=b-a$이므로 $C=\frac{1}{b-a}$가 되어야 한다. 즉, 균등분포의 $\frac{1}{b-a}$는 구간의 길이의 역수라고 볼 수도 있지만, 정규화상수이기도 한 것이다.
적분을 계산하면서 알 수 있듯이, 지시함수 $\mathbf{1}_
{\lbrack a,b\rbrack}(x)$도 $\int_
{-\infty}^{\infty}f_
{X}(x)\space\mathrm{d}x$가 무한대로 발산하지 않고 1이 되도록 돕는다. 즉, PDF를 다룰 때는 정규화상수와 지시함수가 아주 중요한 역할을 한다. 특히 지시함수의 경우 균등분포의 그래프를 그려보면 있고 없고의 차이를 확연히 알 수 있다. 다음과 같은 그림에서, $f(x)$는 균등분포의 PDF인 반면, $g(x)$는 균등분포의 PDF라고 할 수 없다.

위 그림에서는 $a$점과 $b$점에서의 값을 공백처리 했는데, 이는 $X$가 구간 $\lbrack a,b \rbrack$에서 값을 가지기 때문이다, 그런데 연속분포에서 $P(a \le X \le b)=P(a < X < b)$이므로 점 $x=a$나
점 $x=b$에서 확률밀도 값이 $\frac{1}{b-a}$이든 0이든 크게 상관이 없다. 따라서 $X$가 구간 $\lbrack a,b \rbrack$에서 값을 가지는 것을 두고, 구간 $\left( a,b \right)$, $\left( a,b \right]$, $\left[ a,b \right)$에서 값을 가진다고 해도 좋다. 특히 폐구간 $\lbrack a,b \rbrack$과 개구간 $\left( a,b \right)$은 많이 혼용되며 둘 다 $X \sim \mathrm{U}(a,b)$라고 쓴다. 어떤 사람은 폐구간의 경우 좀더 엄밀하게 $X \sim \mathrm{U}\lbrack a,b \rbrack$으로 나타내기도 하지만 실제 응용에서는 큰 의미가 없다고 본다.
이제 균등분포의 CDF를 구해보자. CDF는 PDF아래 넓이이므로 $x<a$일 때 0이고, $x>b$일 때 1이다. $a \le x \le b$일 때는 $x$가 증가할 때 CDF도 선형적으로 증가할 것이다. (일정한 속도로 $a$부터 $b$까지 스캔을 한다고 상상해보자.) 이 부분은 다음과 같이 계산될 것이다.
$$
\int_
{a}^{x} \frac{ \mathbf{1}_
{\lbrack a,b\rbrack}(x)}{b-a} \space \mathrm{d}x=\frac{1}{b-a}\int_
{a}^{x}\mathbf{1}_
{\lbrack a,b\rbrack}(x) \space \mathrm{d}x=\frac{x-a}{b-a}
$$
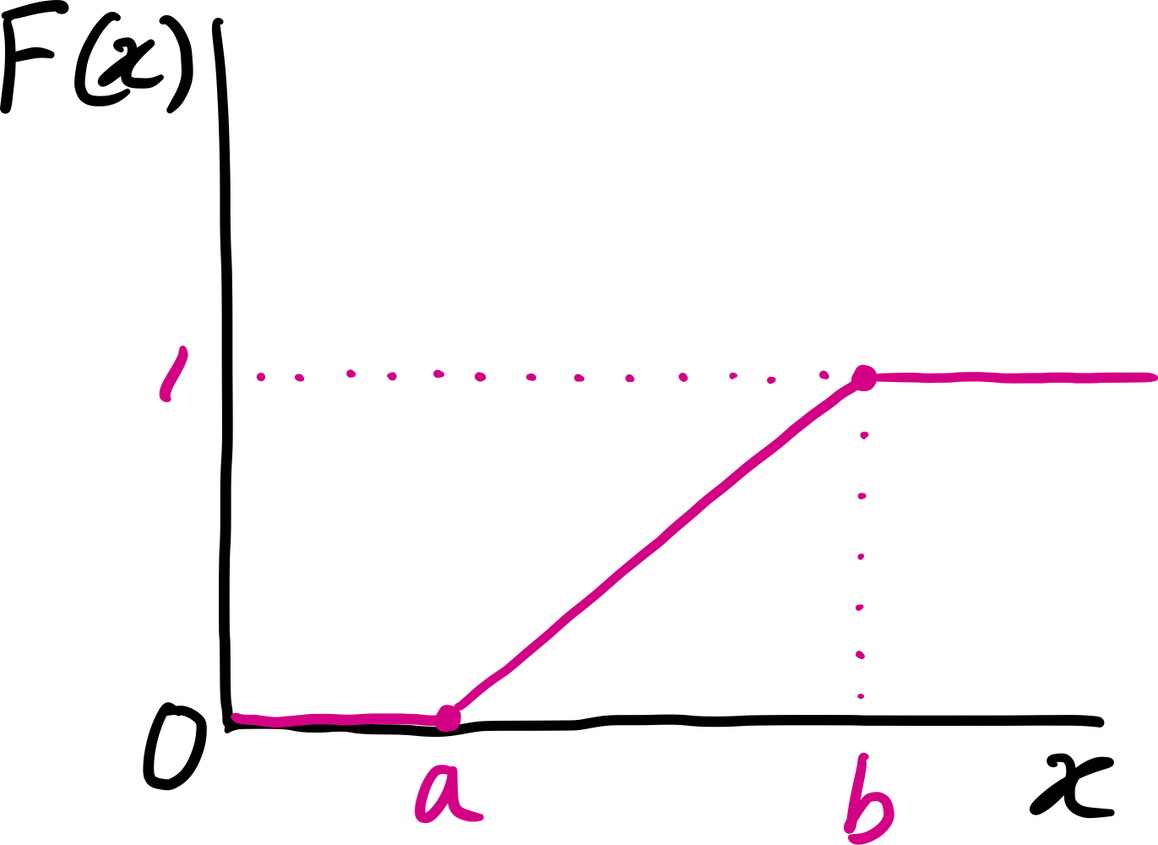
이상을 종합하면, 균등분포 $\mathrm{U}\lbrack a,b \rbrack$의 CDF는 다음과 같다.
$$
F_
{X}(x)=
\begin{cases}
0, &x<a
\\
\frac{x-a}{b-a}, & a \le x \le b
\\
1, & x>b
\end{cases}
$$
균등분포의 CDF 그래프는 다음과 같다. 구간 $\lbrack a,b \rbrack$에서 CDF는 0부터 1까지 선형적으로 증가하는 것을 볼 수 있다.