이번 글에서는 통계학에서 약방의 감초같은 역할을 하는 정규분포를 다루겠다.
#1. 정규분포의 정의
확률변수 $X$가 모수가 $(\mu,\sigma^{2})$인 정규분포(Normal Distribution; 正态分布)를 따를 때, $X \sim \mathrm{N}(\mu,\sigma^{2})$라고 표현하고, $X$는 다음과 같은 PDF를 갖는다:
$$
f_{X}(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{\left(x-\mu\right)^{2}}{2\sigma^{2}}\right)
$$
정규분포의 확률변수 $X$, 모수 $(\mu,\sigma^{2})$는 다음과 같은 의미를 갖는다:
$\space$
$X$: 정규분포를 따르는 확률변수.
$\mu$: 정규분포를 따르는 확률변수의 평균.
$\sigma^{2}$: 정규분포를 따르는 확률변수의 분산.
$\space$
정규분포를 이해하려면 확률변수와 모수를 이해하는 것으로는 부족하고, 우선 유도과정을 알아야 한다.
#2. 정규분포의 유도(개형)
비행기에서 긴급탈출을 위해 뛰어내리는 조종사를 가정해보자. 조종사가 착지할 지표면에 직각좌표계 $xOy$를 설정하자. 조종사는 평면 위의 $(a,b)$지점을 향해 착지하는 것이 목표이다. 물론 그 지점에서 빗나간 곳에 착지할 가능성도 있지만, $(a,b)$지점이 목표이므로 그 지점에 착지하도록 최선을 다한다고 가정하자.
확률변수 $X$와 $Y$를 각각 최종 착지지점의 $x$좌표, $y$좌표라고 두자. 최종 착지지점이 $(x,y)$일 확률밀도는 $f_{(X,Y)}(x,y)$이다. 그런데 $X$와 $Y$는 독립이므로 $f_{(X,Y)}(x,y)=f_X(x)f_Y(y)$가 성립한다.
note: $X$와 $Y$가 독립인 이유가 이해가 되지 않는다면 이런 상황을 상상해보자. 조종사가 $(1,2)$지점으로 떨어졌는데 누군가 와서 “어라, $x$좌표가 1이네요? $x+y=8$이어야 되는데 $y=2$니까 가로로 +5만큼 옮겨드리겠습니다.”라고 한다고 해보자. 이런 어이없는 경우에만 독립이 아니라고 할 수 있다.
목표 착지지점 $(a,b)$와 $x$축 사이의 각도를 $\theta$, 목표 착지지점 $(a,b)$와 원점 $O$사이의 거리를 $r$로 두면, 최종 착지지점 $(x,y)$에 대해 다음이 성립한다.
$$
\begin{split}
(x,y)&=(a+r\cos\theta,b+r\sin\theta),
\\
r^2&=(x-a)^2+(y-b)^2
\end{split}
$$
그러므로 $r$을 관측값으로 갖는 확률변수 $R$의 확률밀도 $f_R(r)$에 대해, 다음이 성립한다.
$$
f_R(r)=f_X(x)f_Y(y)
$$
양변을 $\theta$로 미분하면
$$
\begin{split}
0&=\frac{\mathrm{d}f_X(x)}{\mathrm{d}x}\frac{\mathrm{d}x}{\mathrm{d}\theta}f_Y(y)+f_X(x)\frac{\mathrm{d}f_Y(y)}{\mathrm{d}y}\frac{\mathrm{d}y}{\mathrm{d}\theta}
\\
0&=f^\prime_X(x)(-r\sin\theta)f_Y(y)+f_X(x)f^\prime_Y(y)(r\cos\theta)
\end{split}
$$
여기에 $(x,y)=(a+r\cos\theta,b+r\sin\theta)$을 이용해서 정리하면, 이 미분방정식은 변수분리법으로 쉽게 풀린다.
$$
\begin{split}
f^\prime_X(x)(y-b)f_Y(y)&=f^\prime_Y(y)(x-a)f_X(x)
\\
\frac{f^\prime_X(x)}{(x-a)f_X(x)}&=\frac{f^\prime_Y(y)}{(y-b)f_Y(y)}
\\
\frac{f^\prime_X(x)}{(x-a)f_X(x)}&=C
\\
\frac{f^\prime_X(x)}{f_X(x)}&=C(x-a)
\\
\ln f_X(x)+C_1&=\frac{C}{2}(x-a)^2+C_2
\end{split}
$$
이제 $f_X(x)$에 대해 정리하면
$$
\begin{split}
f_X(x)&=\exp\left(\frac{C}{2}(x-a)^2+C_2-C_1\right)
\\
&=\exp(C_2-C_1)\exp\left(\frac{C}{2}(x-a)^2\right)
\\
&=D\exp\left(\frac{C}{2}(x-a)^2\right),\space D:=\exp(C_2-C_1)
\end{split}
$$
이렇게 $f_X(x)$의 개형을 얻었다. 이제 $f_X(x)$의 정규화상수 $D$를 정하자. $\int_{-\infty}^\infty f_X(x)\space\mathrm{d}x=1$이어야 하므로 $D$는 다음과 같이 계산될 것이다.
$$
D=\frac{1}{\int_{-\infty}^\infty \exp\left(\frac{C}{2}(x-a)^2\right)\space\mathrm{d}x}
$$
문제는 분모인 $\int_{-\infty}^\infty \exp\left(\frac{C}{2}(x-a)^2\right)\space\mathrm{d}x$를 어떻게 계산하는가이다. 여기서 가우스 적분 $\int_{-\infty}^\infty \exp\left(-x^2\right)\space\mathrm{d}x=\sqrt\pi$를 이용해서 계산할 것이다. 그러기 위해서 $C=-k$로 놓자. 적분은 다음과 같이 계산한다.
$$
\begin{split}
&\int_{-\infty}^\infty \exp\left(-\frac{k}{2}(x-a)^2\right)\space\mathrm{d}x
\\
=&\int_{-\infty}^\infty \exp\left(-\frac{k}{2}y^2\right)\space\mathrm{d}y,\space y:=x-a
\\
=&\frac{\sqrt 2}{\sqrt k}\int_{-\infty}^\infty \exp\left(-z^2\right)\space\mathrm{d}z, \space z:=y\sqrt{k/2}
\\
=&\frac{\sqrt {2\pi}}{\sqrt k}
\end{split}
$$
그러므로 $D=\frac{\sqrt k}{\sqrt{2\pi}}$이고, PDF의 개형은 다음과 같다.
$$
f_X(x)=\frac{\sqrt k}{\sqrt{2\pi}}\exp\left(-\frac{k}{2}(x-a)^2\right)
$$
확률변수 $X$는 최종 착지지점이고, $a$는 목표 착지지점이라고 가정했다. 즉, 특정목표 $x=a$을 향해 노력하다보면, 실제 결과인 $X$의 확률밀도는 $f_X(x)=\frac{\sqrt k}{\sqrt{2\pi}}\exp\left(-\frac{k}{2}(x-a)^2\right)$의 형태이다.
그러면 여태 해온 것처럼 $X\sim\mathrm{N}(a,k)$라고 할 수 있을까? 이 경우 모수 $a$는 $X$의 목표이다. 그렇다면 $k$는 무슨 의미일까? 연구가 필요하다. 우선 $k$가 루트안에 있으므로 $k\ge0$이어야 하는 것을 알 수 있다. 그런데 $k=0$일 경우 $f_X(x)$는 항상 0이므로 그렇게 되면 안된다. 따라서 $k>0$인 상수이다.
#3. 정규분포의 모수 확정
함수 $f_X(x)=\frac{\sqrt k}{\sqrt{2\pi}}\exp\left(-\frac{k}{2}(x-a)^2\right)$의 그래프는 어떤 모양일까? 대략적으로만 분석하면 다음과 같다.
$\space$
(1)임의의 $x$에 대해 $f_X(a+x)=f_X(a-x)$가 성립하므로 $x=a$에 대해 대칭이다.
(2) $f^\prime_X(a)=0$이므로 $x=a$일 때 극대값을 갖는다. 극대값은 $f_X(a)=\frac{\sqrt k}{\sqrt{2\pi}}$이다.
(3) $x<a$일 때 $f^\prime_X(x)> 0$이고, $x>a$일 때 $f^\prime_X(x)<0$이므로 그래프의 높이는 $x=a$에서 좌우로 갈 수록 낮아질 것이다.
(4) $\lim_{x\to\pm\infty} f^\prime_X(x)=0$이므로 $x$축을 점근선으로 갖는다.
$\space$
즉, 조종사가 $x=a$를 향해 노력하다보면, $x=a$에서 확률밀도가 제일 높고, 그 주변으로 갈 수록 대칭적으로 낮아질 것이다. 이는 우리의 직관과 부합한다. 그리고 이러한 분포에 대해 다음과 같은 사실을 알 수 있다.
$\space$
(1) 확률분포가 $x=a$에 대해 대칭이므로, $a$는 중앙값(Median; 中位数)이다.
(2) 확률밀도가 $x=a$에서 제일 높으므로, $a$는 최빈값(Mode; 众数)이기도 하다.
$\space$
이 분포는 중앙값, 최빈값까지 모두 $a$로 동일하다. 이제 평균(Mean; 平均)도 $a$라면, 삼위일체 달성이다. 정말 그런지 확인해보자.
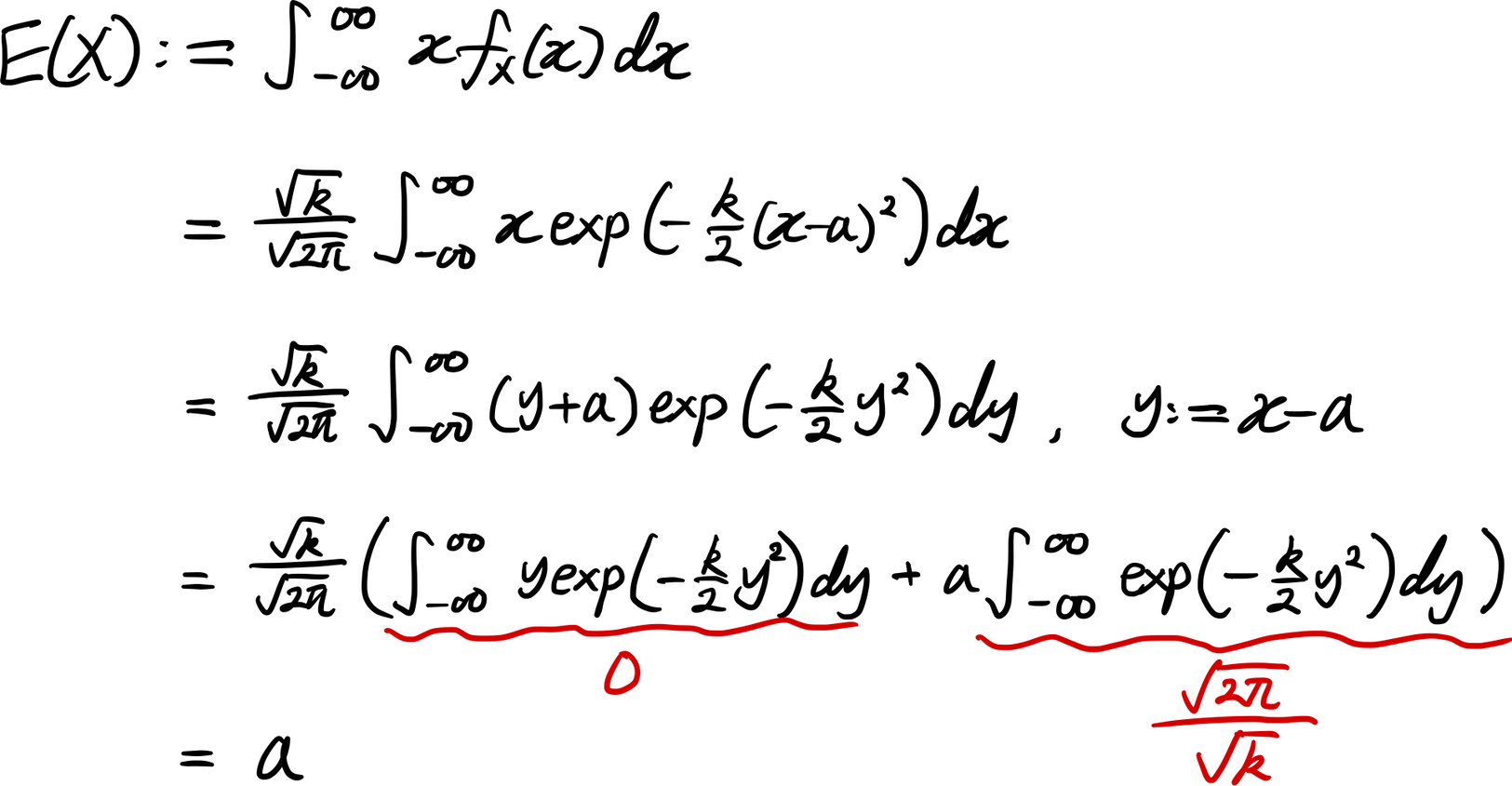
즉, $\mathrm{E}(X)=a$이다. 삼위일체 달성이다. 평균을 구한 김에 분산(Variance; 方差)도 구해보자. 우선 $\mathrm{E}(X^2)$을 구하자.

그러므로 $\mathrm{Var}(X)=\mathrm{E}(X^2)-\left(\mathrm{E}(X)\right)^2=\frac{1}{k}+a^2-(a)^2=\frac{1}{k}$이다. 이로써 상수 $k$의 의미도 자연스럽게 정해졌다. 분산의 역수인 것이다. $k>0$이므로 $\mathrm{Var}(X)>0$이다.
이상의 논의를 종합하면, $f_X(x)$는 다음과 같이 고쳐쓸 수 있다.
$$
f_X(x)=\frac{1}{\sqrt{2\pi\mathrm{Var}(X)}}\exp\left(-\frac{(x-\mathrm{E}(X))^2}{2\mathrm{Var}(X)}\right)
$$
그런데 흔히 $\mathrm{E}(X)=\mu$, $\mathrm{Var}(X)=\sigma^2$로 나타내므로 다음과 같이 쓸 수 있고, 이것이 그 유명한 정규분포 $\mathrm{N}(\mu,\sigma^2)$의 PDF이다.
$$
f_X(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)
$$
#4. 정규분포의 그래프
이제 실제로 정규분포 $\mathrm{N}(\mu,\sigma^2)$의 그래프를 그려보자. 여기서는 $(\mu,\sigma^2)=(0,1)$로 두고 그렸다. 그림에서 빨간 부분은 정규분포의 CDF이다.

그래프는 $x=0$에 대해 대칭이고, 좌우로 갈 수록 밀도가 낮아진다. 점근선은 $x$축이다. 우리가 알아낸 성질이 모두 성립한다. 그 외에도 파란부분이 특별하다는 것을 관찰할 수 있다. 그래프의 좌반부를 보면, 파란부분 이전에는 확률밀도가 체증적으로 증가하지만 파란부분 이후부터 대칭축까지는 체감적으로 증가한다. 즉, 파란부분에 변곡점이 있다. 변곡점을 구하기 위해 $f^{\prime\prime}_X(x)=0$으로 놓으면 $x=\mu\pm\sigma$이다. 즉, 변곡점은 두 개이다. 좌반부에 한 개가 있으므로 우반부에도 대칭적으로 한 개가 있는 것이다.
정리하면, 정규분포 $\mathrm{N}(\mu,\sigma^2)$의 PDF는 다음과 같은 성질을 갖는다.
$\space$
(1) $x=\mu$에 대해 대칭.
(2) $x=\mu$에서 극대값 $\frac{1}{\sigma\sqrt{2\pi}}$을 가짐.
(3) $x<\mu$일 때 증가, $x>\mu$일 때 감소.
(4) $x$축을 점근선으로 가짐.
(5) 변곡점 $x=\mu\pm\sigma$이 존재.
#5. 표준정규분포와 오차함수
정규분포 중에서도 $\mathrm{N}(0,1)$은 비교적 간단하기 때문에 특히 많이 쓴다. 이를 z-분포(z-Distribution; z-分布)라고 한다.
한편, 임의의 확률변수 $X$에 대해, 평균 $\mathrm{E}(X)=\mu$, 분산 $\mathrm{Var}(X)=\sigma^2$으로 두면, $Z=\frac{X-\mu}{\sigma}$에 대해 다음이 성립한다.
$$
\begin{split}
\mathrm{E}\left(Z\right)&=\frac{1}{n}\sum_{i=1}^{n}\frac{X_i-\mu}{\sigma}
\\
&=\frac{1}{\sigma}\left(\frac{1}{n}\sum_{i=1}^{n}X_i-\frac{1}{n}\cdot n\mu\right)
\\
&=\frac{1}{\sigma}(\mu-\mu)
\\
&=0,
\end{split}
$$
$$
\begin{split}
\mathrm{Var}\left(Z\right)&=\frac{1}{n}\sum_{i=1}^{n}\left(\frac{X_i-\mu}{\sigma}-\mathrm{E}\left(\frac{X-\mu}{\sigma}\right)\right)^2
\\
&=\frac{1}{n}\sum_{i=1}^{n}\frac{\left(X_i-\mu\right)^2}{\sigma^2}
\\
&=\frac{1}{\sigma^2}\cdot\frac{1}{n}\sum_{i=1}^{n}(X_i-\mu)^2
\\
&=\frac{1}{\sigma^2}\cdot\sigma^2
\\
&=1
\end{split}
$$
이 새로운 확률변수 $Z$를 원래의 확률변수 $X$의 표준화 확률변수(Standardized RV; 标准化随机变量)라고 한다. 따라서 평균이 0이고 분산이 1인 정규분포 $\mathrm{N}(0,1)$은 표준화 확률변수의 분포라고 볼 수 있으므로 표준정규분포(Standard Normal Distribution; 标准正态分布)라고도 한다. 일반적으로 정규분포를 따르는 $X$를 연구하고 싶을 때는 그것을 표준화해서 $Z=\frac{X-\mu}{\sigma}$를 대신 연구하는 것이 보통이다.
표준정규분포의 PDF는 $\phi$를, CDF는 $\Phi$를 써서 나타낸다. 즉, 다음과 같이 쓴다.
$$
\begin{split}
\phi_Z(z)&=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{z^2}{2}\right)
\\
\Phi_{Z}(z)&=\int_{-\infty}^{z}\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{t^2}{2}\right)\space\mathrm{d}t
\end{split}
$$
여기서 많이 쓰이는 $\Phi_Z(z)$를 간단히하기 위해, 오차함수(Error Function; 误差函数) $\mathrm{erf}(z)$를 다음과 같이 정의한다.
$$
\mathrm{erf}(z):=\int_{0}^{z}\frac{2}{\sqrt{\pi}}\exp\left(-t^2\right)\space\mathrm{d}t
$$
그러면 $\Phi_Z(z)$를 다음과 같이 깔끔하게(?) 정리할 수 있다.
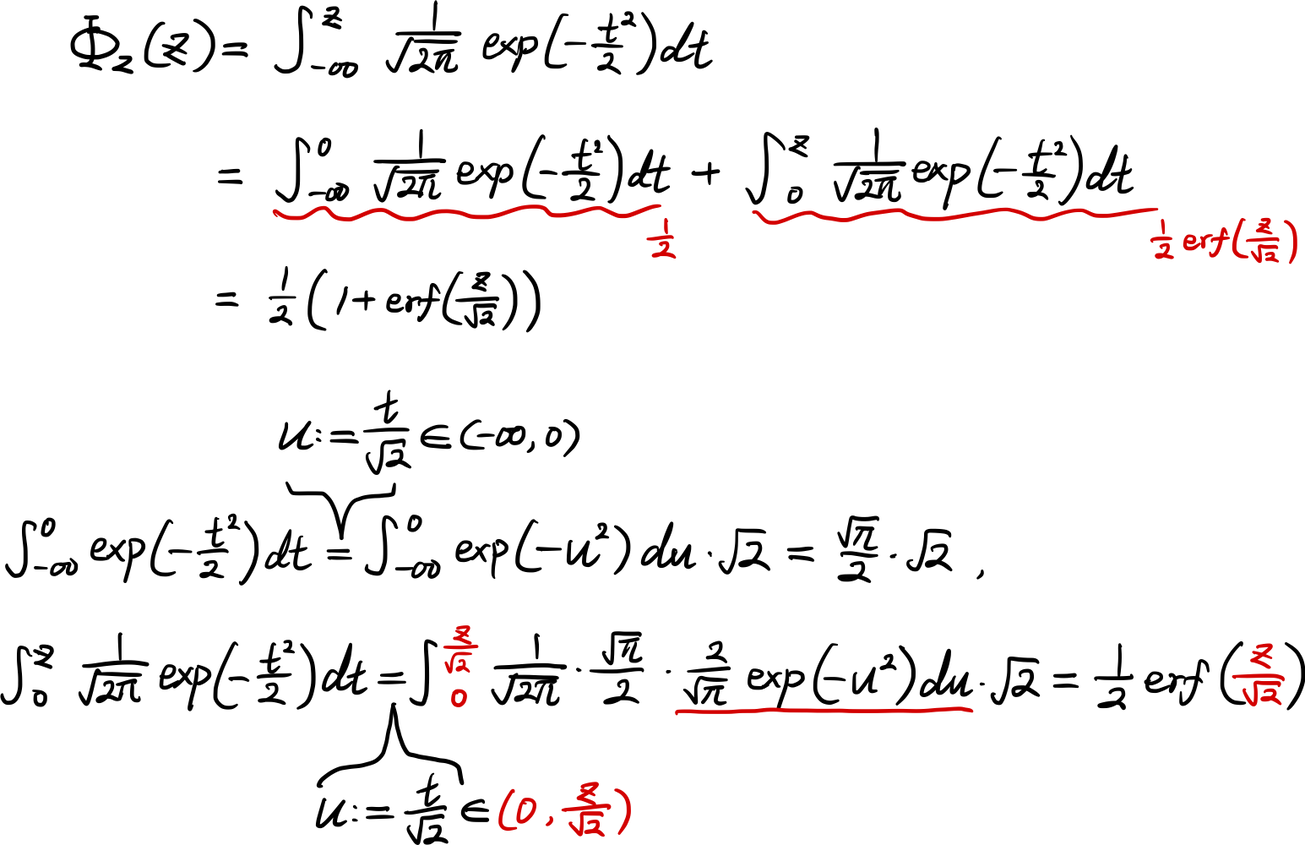
$\Phi_Z(z)=\frac{1}{2}\left(1+\mathrm{erf}\left(\frac{z}{\sqrt{2}}\right)\right)$이고, $z=\frac{x-\mu}{\sigma}$이므로, 일반적인 정규분포에 대해서는 다음과 같은 CDF를 얻는다.
$$
F_X(x)=\Phi_Z(\frac{x-\mu}{\sigma})=\frac{1}{2}\left(1+\mathrm{erf}\left(\frac{x-\mu}{\sigma\sqrt{2}}\right)\right)
$$
한편, 오차함수의 그래프는 다음과 같이 아름다운 S의 형태이다. 그러므로 이렇게 생긴 그래프를 시그모이드(Sigmoid) 곡선이라고 부르고, 시그모이드 곡선을 그래프로 가지는 함수를 시그모이드 함수라고 한다. 시그모이드 함수는 여러 종류가 있으며 오차함수는 시그모이드 함수 중 하나이다.

note1: 시그모이드 곡선은 인공신경망에서 활성함수(Activation Function; 激活函数)를 모델링하는 데 쓰인다. $\mathrm{erf}(z)$는 복잡하므로 표준 로지스틱 함수(Standard Logistic Function) $f(x)=\frac{1}{1+e^{-x}}$를 대신 가져다 쓴다. 표준 로지스틱 함수도 시그모이드 함수이다.
note2: 오차함수라는 이름은 이 함수가 확률변수의 오차를 연구하는 데 쓰였기 때문이다. 정규분포도 오차를 연구하는 데 쓰였다. 당장 정규분포의 유도과정을 되짚어 보면, 어떤 특정한 목표가 있고, 그것을 향해 노력하는 도중 오차가 발생함을 알 수 있다.
#6. 정규분포의 의미
정규분포는 왜 ‘정규’분포라고 부를까? 영어로는 Normal 분포인데, 왜 정규분포를 두고 Normal하다고 할까? 그 이유는 인간이 어떤 일을 할 때, 특정한 목표를 가지고 노력하는 것이 Normal하기 때문이라고 생각한다.
예를 들어 라면을 끓일 때 물을 정확히 500 ml을 맞추려 노력한다고 해보자. Normal한 경우, 500 ml일 확률밀도가 제일 높고, 그 주위로 약간의 오차가 있어서 501 ml일 수도 있고, 499 ml일 수도 있는 것이다. 하지만 그 확률밀도는 500 ml 근방에서보다 낮을 것이다. 이 경우 오차가 0일 확률밀도가 제일 높고, $\pm$로 갈 수록 낮아진다. 이런 상황에서 자연스럽게 정규분포가 유도된다. 조종사의 착륙지점의 $x$좌표를 라면물의 부피로 바꿨을 뿐이다. 이 외에도, 각목을 $x$ cm의 길이로 가공하거나, 상품의 무게를 $y$ g이 되게 끔 포장한다는 등 여러 상황에서 정규분포는 자연스럽게 도출될 것이다.
정규분포는 통계학에서 약방의 감초같은 역할을 하며, 수많은 자연현상과 사회현상을 나타내는 데 쓰이는데, 이것은 정규분포가 특정 목표를 정하고 그것을 향해 노력하는 과정에서 자연스럽게 유도되는 분포이기 때문이다.
note1: 정규분포가 통계학에서 중요한 위치를 차지하는 이유는 중심극한정리(Central Limit Theorem, CLT; 中心极限定理) 때문인 것도 있다.
note2: 정규분포는 가우스 분포(Gaussian Distribution; 高斯分布)라고도 한다. 독일 수학자 카를 프리드리히 가우스(Carl Friedrich Gauss)의 이름을 따왔다. 이미지 처리분야에서 가우시안 블러가 바로 이 가우스 분포를 사용한다. 가우스분포와 이미지를 합성곱 연산을하면 이미지가 부드러워지는 원리를 이용하는 것이다.


