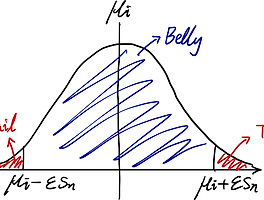
지난 글에서 소개한 중심극한정리는 안쓰이는 데가 없다고 할 정도로 광범위하게 응용된다. 몇가지 관련 예제와 해결법을 생각해보았고, 따로 정리한다.
CLT 응용의 첫번째 핵심은 분포를 몰라도 문제해결에 지장이 없다고 과감하게 생각하는 것이다. 린데베르그 조건을 만족하면 중심극한정리가 성립하는데, 독립항등분포이면 무조건 만족하고, 독립항등분포는 아니더라도 독립이고, 극단적인 상황의 분산이 무시할 수 있을만큼 작다면 역시 만족한다. 후자의 경우, 심리학에서 인간의 IQ가 정규분포를 따른다고 가정한다는 예시를 논의했다. 독립항등분포나 극단적인 상황을 무시하는 것은 어떤 수학적 모델을 만드는데 흔히 깔고가는 가정이고, 따라서 CLT는 항상 성립한다고 봐도 무방하다. 이런 마인드를 갖고 몇가지 예제를 생각해보았다.
CLT 응용의 두번째 핵심은 확률변수의 합에 관한 확률을 표준정규분포에 관한 확률로 고쳐쓰는 것이다. 왜 하필 표준정규분포인가? 표준정규분포는 z분포로도 불리며 일반적인 정규분포보다 계산이 비교적 용이하기 때문에 z분포표라는 표가 있다. z분포표는 표준정규분포의 누적분포함수인 $\Phi(z):=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{z}e^{-x^2/2}\space dx$의 값을 수학자들이 계산해서 기록해 놓은 표다. 이 표를 보고 바로 특정 $\Phi(z)$값을 알아낼 수 있다. ($z$는 소수점 2자리, $\Phi(z)$는 4~5자리까지.) (z분포표 링크)
#1. 품질검사의 합격률
문제) 어떤 물건은 10개의 작은 부품을 이어 붙여 만드는데, 각 부품의 길이는 $2\pm0.05$라고 하자. 물건의 총길이가 $20\pm0.1\space\mathrm{mm}$일 때 품질검사에서 합격이라고 가정하면, 합격률은?
해결) 각 부품의 길이를 확률변수 $X_i(i=1,2,\cdots,10)$으로 놓자. 기댓값의 선형성에 의해,
$$ \mathbb{E}\left(\sum X_i\right)=\sum\mathbb{E}(X_i)=10\times2=20 $$
그리고 일반적으로 각 부품의 생산은 독립적이므로
$$ \mathrm{Var}\left(\sum X_i\right)=\sum\mathrm{Var}(X_i)=10\times0.05^2=25/1000 $$
$X_i$가 린데베르그 조건을 만족하면 중심극한정리가 성립한다.
$$ \begin{split} &P\left(20-0.1\le\sum X_i\le20+0.1\right) \\&=P\left(-0.63\le\frac{\sum X_i-20}{\sqrt{25/1000}}\le0.63\right) \\&\approx\Phi(0.63)-\Phi(-0.63)=0.7357-0.2643=0.4714 \end{split} $$
#2. 사내 비품의 적절한 수량
문제) 200명의 직원이 있는 회사에서 각 직원이 프린터를 쓸 확률은 5%이라고 하자. 최소 90%의 확률로 직원이 프린터가 필요할 때마다 반드시 쓸 수 있도록 보장하려면 최소 몇 대의 프린터가 비치되어야할까?
해결) 위 문제와는 다르게 먼저 확률을 정하고 ($\Phi(z)$ 값), 그에 맞는 $z$를 찾아야 한다.
각 직원이 프린터를 쓰느냐 마느냐는 베르누이 독립시행으로 볼 수 있고, 직원이 200명이므로 동시에 쓰이는 프린터의 수 $X$는 $\mathrm{Bin}(200,0.05)$를 따르며, $\mu=10$, $\sigma^2=9.5$이다.
이제 실제로 필요한 프린터의 수, 즉 실제로 동시에 쓰이는 프린터의 수를 $x$로 놓으면, 문제의 요구를 만족하려면 $P(X\le x)\ge0.9$여야 한다. $\mathrm{Bin}(200,0.05)$의 누적분포함수는 계산하기 복잡하므로 대신 이항근사를 이용하자.
드 무아브르-라플라스 정리에 의해,
$$ P(X\le x)=P\left(\frac{X-10}{\sqrt{9.5}}\le\frac{x-10}{\sqrt{9.5}}\right)\approx\Phi\left(\frac{x-10}{\sqrt{9.5}}\right)\ge0.9 $$
$(x-10)/\sqrt{9.5}\ge1.28$ 정도면 위 부등식을 만족한다. 따라서 $x\ge 13.945$이면 직원들의 프린터기 수요를 충족하므로 적절한 프린터의 수는 $x=14$이다.
#3. 학원광고를 믿어 말어?
문제) 어떤 학원이 합격률이 80%라고 광고하고 있다. 나는 학원 근처를 지나가는 사람 100명을 무작위로 골라 이 학원에 다녔는지, 실제로 시험에 합격했는지 물어볼 것이다. 그 결과 학원에 다닌 100명 중 80명은 아니더라도, 75명 정도가 합격했다면 저 광고를 믿기로 마음먹었다. 실제로는 학원의 합격률이 70% 밖에 안 된다고 할 때, 내가 저 광고를 믿어야할 확률은?
해결) 100명의 응답을 $X_i(i=1,2,\cdots,100)\sim\mathrm{Bern}(0.7)$로 놓자. 내가 저 광고를 믿을 확률은 $P(\sum X_i>75)$이다. 한편, $\sum X_i\sim\mathrm{Bin}(100,0.7)$이므로 드 무아브르-라플라스 정리에 의해,
$$ \begin{split} &P\left(\sum X_i>75\right)=1-P\left(\sum X_i\le75\right) \\&\approx1-\Phi\left(\frac{75-100\cdot0.7}{\sqrt{100\cdot0.7\cdot0.3}}\right)=1-\Phi(1.09)=0.1379 \end{split} $$
즉, 13.79% 밖에 안 된다. 이렇게 신뢰도가 낮은 이유는 혹시 합격률을 10% 올려치기 했기 때문인가? 실제로 학원의 합격률이 80%이고 정직하게 광고했다면, 어떨까?
$$ \begin{split} &P\left(\sum X_i>75\right)=1-P\left(\sum X_i\le75\right) \\&\approx1-\Phi\left(\frac{75-100\cdot0.8}{\sqrt{100\cdot0.8\cdot0.2}}\right)=1-\Phi(-1.25)=0.8944 \end{split} $$
실제로 합격률이 80%이면 신뢰도는 89.44%이다. 학원이 10%만 올려치기 했을 뿐인데도 내가 느끼는 신뢰도를 대폭 깎아먹었다. 만약 20%를 올려쳐서 90%라고 광고하면 나는 100명 중 85명 정도로 믿음의 기준을 수정할 것이고, 학원의 신뢰도는 박살이 날 것이다.
$$ \begin{split} &P\left(\sum X_i>85\right)=1-P\left(\sum X_i\le85\right) \\&\approx1-\Phi\left(\frac{85-100\cdot0.7}{\sqrt{100\cdot0.7\cdot0.3}}\right)=1-\Phi(3.27)=0.0006 \end{split} $$
물론 믿음의 기준을 수정하지 않는다면 신뢰도는 $0.1379$로 변하지 않는다.