확률변수 $X_i(i=1,2,\cdots)$에 대해 다음이 성립하면 $X_i$는 중심극한정리(Central Limit Theorem, CLT; 中心极限定理)를 따른다고 표현하고, 기호로는 $X_i\in\mathrm{CLT}$와 같이 나타낸다.
$$ \frac{\sum_{i=1}^{n}X_i-\mathbb{E}\left(\sum_{i=1}^{n}X_i\right)}{\sqrt{\mathrm{Var}(\sum_{i=1}^{n}X_i)}}\overset{d}{\to}Z\sim\mathrm{N}(0,1) $$
뭔가 복잡해 보이지만 차근차근 분석하면 어려울 것도 없다. 좌변의 분수는 사실 확률변수 $X_i$의 합을 표준화한 것이다. (Box-Muller 변환 참조.) 표준화는 확률변수의 평균을 0, 분산을 1로 만드므로 수렴하는 분포의 평균과 분산이 각각 0과 1임은 자명하다.
따라서 중심극한정리는 확률변수의 합을 표준화하면 표준정규분포를 따르는 확률변수에 분포수렴한다는 뜻을 담고 있다. (확률변수의 수렴 참조.)
표준화된 확률변수를 $X^{\ast}$와 같이 나타내자. 그러면 ‘확률변수의 합을 표준화한 것’은 다음과 같이 나타낼 수 있고,
$$ \left(\sum_{i=1}^{n}X_i\right)^{\ast}:=\frac{\sum_{i=1}^{n}X_i-\mathbb{E}\left(\sum_{i=1}^{n}X_i\right)}{\sqrt{\mathrm{Var}(\sum_{i=1}^{n}X_i)}} $$
중심극한정리를 다음과 같이 간단하게 표현할 수 있다.
$$ \left(\sum_{i=1}^{n}X_i\right)^{\ast}\overset{d}{\to}Z\sim\mathrm{N}(0,1) $$
note: 확률변수의 합을 표준화하지 않아도 좋다. 표준화하지 않은 확률변수의 합은 정규분포 $\mathrm{N}(n\mu,n\sigma^2)$에 분포수렴한다. 물론 이때는 각 확률변수의 평균과 분산이 일치한다는 가정이 들어가야 된다. 어찌됐든 하나의 분포로 수렴하기 때문이다.
큰 수의 법칙과 마찬가지로, 임의의 확률변수의 수열이 중심극한정리를 따르려면 특정한 조건이 필요하고, 이 특정한 조건을 제시함으로써 여러 수학자들의 이름이 붙은 파생정리가 나온다. 비교적 유명한 것으로는 린데베르그-레비 정리(Lindeberg-Levy; 林德伯格-勒维)와 드 무아브르-라플라스(De Moivre-Laplace; 棣莫弗-拉普拉斯) 정리가 있다.
#1. 린데베르그-레비 정리
#1-1. 내용
i.i.d. $X_i(i=1,2,\cdots)$의 기댓값이 $\mu$, 분산이 $0<\sigma<\infty$일 때, $X_i\in\mathrm{CLT}$, i.e.
$$ \left(\sum_{i=1}^{n}X_i\right)^{\ast}=\frac{\sum_{i=1}^{n}(X_i-\mu)}{\sqrt{n}\sigma}=\frac{1}{\sqrt{n}}\sum_{i=1}^{n}X_i^{\ast}\overset{d}{\to}Z\sim\mathrm{N}(0,1) $$
린데베르그-레비의 정리는 $X_i$가 독립항등분포를 따를 것과 분산의 유계성을 가정하고 있다. 분모에 분산이 위치해야 하므로 분산이 0이 되어서는 안 된다는 것은 자명하다. 또는 ‘분산이 0이면 $X$는 거의 확실히 상수이므로 합을 구한들 그것은 정규분포가 아니라 상수일 것이다.’라고 이해해도 좋겠다.
린데베르그-레비 정리의 핵심은 중심극한정리가 분포의 종류를 가리지 않고 전반적으로 적용된다는 것이다. 독립항등분포이고 기댓값과 분산이 유한하면 중심극한정리가 성립한다.
중심극한정리가 성립한다는 것은 합의 분포가 정규분포로 수렴한다는 것이다. 바로 지난 글에서 Irwin-Hall 분포가 좋은 예시이다. Irwin-Hall 분포는 $n=12$일 때 정규분포와 ‘가깝다’고 했다. (해당 글 참조.) 이제 ‘가깝다’는 표현대신 중심극한정리의 문법으로 서술해보자.
i.i.d. $U_i\sim\mathrm{U}(0,1)$의 평균을 구해보면 $\frac{1}{2}$이고, 분산은 $\frac{1}{12}$이므로 $U_i\in\mathrm{CLT}$이면
$$ \frac{\sum_{i=1}^{n}U_i-\frac{n}{2}}{\sqrt{n}\sqrt{\frac{1}{12}}}\overset{d}{\to}Z\sim\mathrm{N}(0,1) $$
#1-2. 린데베르그 조건
여기서 만약 독립항등분포라는 가정을 빼면 어떨까? 또, 분산이 무한대로 발산하면 어떨까? 이 경우는 좀 더 널널한 조건의 중심극한정리가 될 것이다.
린데베르그는 서로 독립인 $X_i$가 중심극한정리를 따르려면 특별한 조건(린데베르그 조건)을 만족해야한다는 것을 증명했는데, 그 조건은 다음과 같다. (서로 같은 분포일 필요도 없고, 분산이 발산해도 된다.)
$$ \begin{split} &\forall\epsilon>0:\lim_{n\to\infty}\frac{\sum_{i=1}^{n}T_i^2(\epsilon)}{s_n^2}=0, \\[2ex] &T_i^2(\epsilon):=\mathbb{E}[(X_i-\mu_i)^2\cdot\mathbf{1} {\lbrace\vert X_i-\mu_i\vert\ge\epsilon s_n\rbrace}] \\ &s_n^2:=\mathrm{Var}\left(\sum_{i=1}^n X_i\right)=\sum_{i=1}^{n}\mathrm{Var}(X_i) \end{split} $$
아래 그림처럼, 식에서 $T_i^2(\epsilon)$는 분포의 꼬리(Tail; 尾部) 부분의 분산정도로 이해할 수 있다. 한편, $s_n^2$은 ‘분포의 전체의 분산을 합한 것’이므로, 린데베르그 조건은 ‘분포 꼬리의 분산의 총합이 분포 전체의 분산의 총합에서 차지하는 비중이 0’으로 해석하면 되겠다. 즉, $n$이 매우 클 때 분포의 꼬리를 무시하고 나머지(중간 부분)만 고려할 수 있다는 의미가 담겨 있는데, 이는 정규분포의 특징과도 유사하다.
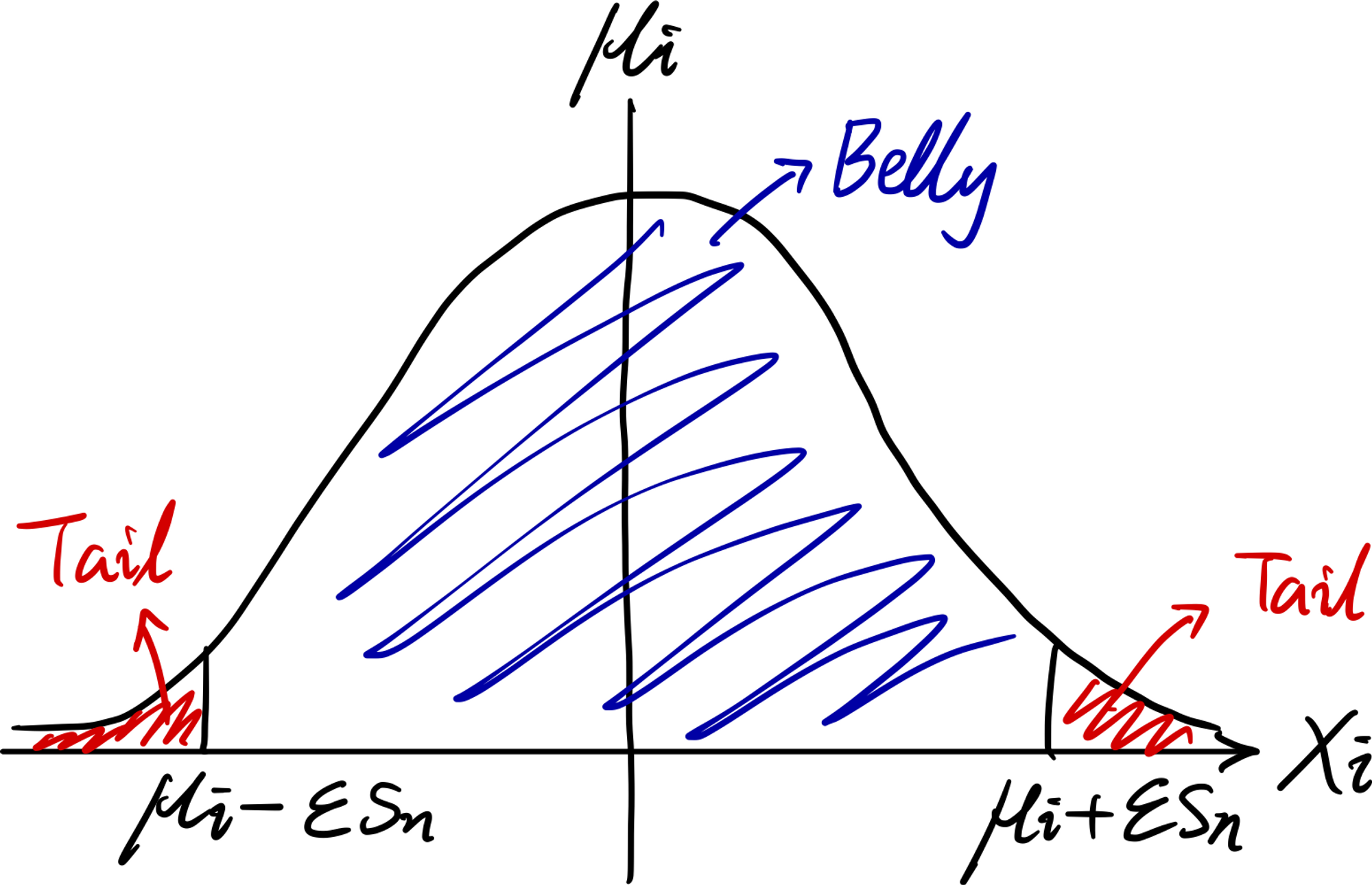
note: ‘분모와 분자가 모두 발산하는데 분수의 극한이 0’이라는 것은 ‘분모의 증가속도가 분자의 증가속도를 압도한다’고 해석할 수 있다. 란다우 표기법(Landau Notation; 朗道符号)를 이용하면 $\sum_{i=1}^{n}T_i^2(\epsilon)=o(s_n^2)$ 이나 $\sum_{i=1}^{n}T_i^2(\epsilon) \lll s_n^2$으로 표현할 수 있겠다.
$X_i$가 독립항등분포를 따른다는 조건이 주어지면 린데베르그 조건이 쉽게 만족된다. 기댓값을 $\mu$, 분산을 $\sigma^2$으로 놓으면, 전체 분산의 총합은 $n\sigma^2$이 되고, $n\to\infty$일 때 $\infty$로 발산한다. 한편, 꼬리 분산의 총합은 점점 줄어든다. 따라서 분수의 극한은 0이된다.
결국 중심극한정리가 성립하는 조건을 다음과 같이 요약할 수 있다.
(1) 분산이 무한대로 발산하더라도 독립항등분포이면 중심극한정리가 성립한다.
(2) 독립항등분포가 아니더라도 린데베르그 조건을 만족하면 중심극한정리가 성립한다.
#1-3. 린데베르그 조건의 의의
(1) IQ가 정규분포를 따른다?
큰 수의 법칙과 마찬가지로, 중심극한정리도 통계학 전반에서 응용되는 법칙인데, 흔히 사회과학분야에서 정규분포를 가정하는 것이 좋은 예시이다.
심리학에서는 사람의 IQ가 정규분포를 따른다고 가정하는데, IQ의 측정에 대해서는 여러 의견이 있지만, 대체로 여러 독립된 요소의 가중합이라는 의견이 지배적이다. IQ를 구성하는 여러 요소인 환경요소, 교육정도, 부모의 유전자 등의 확률변수들은 어떤 분포를 따른 것이고, 이 분포들의 꼬리, 즉 극단적인 값들의 영향은 극히 미미할 것이다. 결국 이 독립된 요소들은 린데베르그 조건을 쉽게 만족하며, IQ가 정규분포를 따른다고 가정할 수 있다.
IQ뿐만 아니라, 여러 사회적 변수들 역시 같은 논리로 정규분포를 따른다고 가정한다.
(2) 각종 검정법의 탄생
표본평균이나 표본분산 같은 통계량과 이를 이용한 각종 검정 역시 정규분포와 연관되어 있다. 중심극한정리에 의해, 어떤 분포를 따르는 모집단에서 추출하여 얻은 표본의 평균 $\overline{X}$에 대해 $\overline{X}\overset{d}{\to}\mathrm{N}(\mu,\sigma^2/n)$이고, 이는 모집단이 어떤 분포이든 상관없다. 표본을 뽑을 때 이미 독립항등분포가 가정되어 린데베르그 조건을 만족하기 때문이다.
표본평균이 정규분포를 따르므로 이것을 표준화한 $Z$에 대해 $Z:=\frac{\overline{X}-\mu}{\sqrt{\sigma^2/n}}\overset{d}{\to}\mathrm{N}(0,1)$이 성립하고, z분포에 의한 z검정을 가능하게 한다. 뿐만 아니라 t검정에 사용되는 t분포, 그리고 표본분산과 관련된 카이제곱 검정과 카이제곱 분포, F검정과 F분포 모두 z분포에서 파생되므로 중심극한정리는 통계학에 있어 심장과도 같은, 아주 중요한 정리라고 할 수 있다. (관련 내용 추후 작성 예정.)
#2. 드 무아브르-라플라스 정리
#2-1. 내용
i.i.d. $X_i(i=1,2,\cdots)\sim\mathrm{Bern}(p)(0<p<1)$일 때, $X_i\in\mathrm{CLT}$, i.e.
$$ \frac{\sum_{i=1}^{n}X_i-np}{\sqrt{np(1-p)}}\overset{d}{\to}Z\sim\mathrm{N}(0,1) $$
여기서 확률변수의 합 $\sum_{i=1}^{n}X_i$는 이항분포 $\mathrm{Bin}(n,p)$를 따르므로, 드 무아브르-라플라스 정리는 흔히 이항분포의 정규근사(Normal Approximation; 正态近似)라고도 한다.
드 무아브르-라플라스 정리를 분포수렴의 정의를 이용하여 실제 응용에 적합한 형태로 수정하면 다음과 같다. 여기서 $\Phi(z):=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{z}e^{-x^2/2}\space dx$는 표준정규분포 $\mathrm{N}(0,1)$의 누적분포함수이고, $X:=\sum_{i=1}^{n}X_i$이다.
$$ \lim_{n\to\infty}P\left(a\le\frac{X-np}{\sqrt{np(1-p)}}\le b\right)=\Phi(b)-\Phi(a) $$
#2-2. 유도
응용의 형태를 잘 보자. 드 무아브르-라플라스 정리가 말하고자 하는 것은 이항분포의 모수 $n$이 충분히 크다면 정규분포에 근사할 수 있다는 사실이다.
이 사실을 지난 글에서 그래프를 통해 확인했다. (이항분포 참조.) 이번에는 이 정리를 수학적으로 유도해보기로 하자. 유도과정을 요약하자면, 이항분포의 확률질량함수를 계승을 포함한 형태로 고쳐쓰고, 계승의 근사치를 구하는 방법 중 하나인 스털링 근사를 적용하는 것이다.
note: 사실 $X_i$가 독립항등분포를 따른다는 사실에서 이미 게임 끝이다. 린데베르그 조건을 만족하므로 중심극한정리가 성립하기 때문. 하지만 이러면 너무 간단하므로 이 조건을 모른다고 가정하고 다른 방식으로 유도해보자. 실제로 린데베르그 조건이 나중에 알려졌다.
먼저 이항분포의 확률질량에 스털링 근사를 대입하여 다음과 같이 정리한다. 식을 간단히 쓰기 위해 $q:=1-p$로 놓자.
$$ \begin{split} &{n\choose x}p^xq^x=\frac{n!}{x!(n-x)!}p^xq^{n-x} \\ &\approx\frac{\sqrt{2\pi n}(n^{n}e^{-n})}{\sqrt{2\pi x}(x^{x}e^{-x})\sqrt{2\pi (n-x)}((n-x)^{n-x}e^{-(n-x)})} \\ &=\sqrt{\frac{n}{2\pi x(n-x)}}\left(\frac{np}{x}\right)^x\left(\frac{nq}{n-x}\right)^{n-x} \end{split} $$
식을 두 부분으로 나누어 처리하자. 다음과 같이 정의하자.
$$ \begin{split} &f(x):=\sqrt{\frac{n}{2\pi x(n-x)}} \\ &g(x):=\left(\frac{np}{x}\right)^x\left(\frac{nq}{n-x}\right)^{n-x} \end{split} $$
$f(x)$를 우선 처리해보자. $z=\frac{x-np}{\sqrt{npq}}$으로 놓으면 $x=np+z\sqrt{npq}$이다. $n\to\infty$일 때, 뒤의 루트항의 증가속도가 빠르지 않으므로 생략되어 $x\approx np$이고, $n-x\approx nq$이다. 따라서
$$ f(x)=\sqrt{\frac{n}{2\pi x(n-x)}}\approx\sqrt{\frac{1}{2\pi n pq}}=\frac{1}{\sqrt{2\pi}\sqrt{npq}} $$
$g(x)$는 지수 부분에 변수가 위치하므로 로그를 이용하여 처리해보자. 우선 $g(x)$ 대신 $\ln g(x)$를 구하려고 한다. 로그식을 정리할 때 테일러 정리에 의해 $\ln(1+x)\approx x-\frac{x^2}{2}$이 성립함을 이용하자. (역시 2차항까지만 전개하는 것이 포인트다.)
$$ \begin{split} &\ln\left(\frac{np}{x}\right)^x=x\ln\left(\frac{np}{x}\right)=x\ln\left(1-\frac{z\sqrt{npq}}{x}\right) \\ &\approx x\left(-\frac{z\sqrt{npq}}{x}-\frac{z^2 npq}{2x^2}\right)=-z\sqrt{npq}-\frac{z^2}{2}\cdot\frac{npq}{x}, \\[5ex] &\ln\left(\frac{nq}{n-x}\right)^{n-x}=(n-x)\ln\left(\frac{nq}{n-x}\right)=(n-x)\ln\left(1+\frac{z\sqrt{npq}}{n-x}\right) \\ &\approx (n-x)\left(\frac{z\sqrt{npq}}{n-x}-\frac{z^2 npq}{2(n-x)^2}\right)=z\sqrt{npq}-\frac{z^2}{2}\cdot\frac{npq}{n-x} \end{split} $$
이 결과와 $x\approx np$, $n-x\approx nq$를 대입하면, $\ln g(x)$와 $g(x)$를 구할 수 있다.
$$ \begin{split} &g(x)=\left(\frac{np}{x}\right)^x\left(\frac{nq}{n-x}\right)^{n-x} \\ &\ln g(x)=\ln\left(\frac{np}{x}\right)^x+\ln\left(\frac{nq}{n-x}\right)^{n-x}\approx-\frac{z^2}{2}\cdot\frac{n\cdot npq}{x(n-x)}\approx-\frac{z^2}{2} \\ &\therefore g(x)\approx \exp\left({-\frac{z^2}{2}}\right)=\exp\left(-\frac{(x-np)^2}{2npq}\right) \end{split} $$
따라서 다음 근사식이 성립한다. 즉 $\mathrm{Bin}(n,p)$는 $\mathrm{N}(np,npq)$에 근사시킬 수 있다. 정규분포의 모수인 $np$와 $npq$가 각각 이항분포의 평균과 분산이므로 $\mathrm{Bin}(n,p)$를 따르는 확률변수를 표준화하면 $\mathrm{N}(0,1)$에 근사시킬 수 있다.
$$ {n\choose x}p^xq^x\approx\frac{1}{\sqrt{2\pi}\sqrt{npq}}\exp\left(-\frac{(x-np)^2}{2npq}\right) $$
#2-2. 정규근사 vs 푸아송 근사
지난 글에서 이항분포는 푸아송 분포로 근사할 수 있음을 보였다. (푸아송 분포 참조.) 애초에 푸아송 분포 자체가 이항분포에 극한을 취하면서 생겼다고 보는 것이 맞다.
그렇다면 이항분포는 근사방법이 정규근사와 푸아송 근사 두 가지가 있는 셈인데, 이 둘의 차이는 무엇일까? 어떨 때 정규근사를 써야하고 어떨 때 푸아송 근사를 써야 할까? 다음 그림으로 요약하자.

먼저 정규근사를 논의해보자. 이항분포는 서로 독립인 베르누이 확률변수의 합으로 이루어져 있다. 따라서 독립항등분포 조건이 충족되어 항상 린드베르그 조건을 만족한다.
그렇다면 각 베르누이 확률변수의 분산이 0만 아니면 이항분포는 정규분포로 분포수렴한다. 분산이 0이면 확률변수는 거의 확실히 상수이기 때문이기도 하고, 이는 중심극한정리 식의 분모에 분산이 들어간다는 사실로도 설명 가능하다. 이항분포의 분산은 $np(1-p)$이므로 $p\not=0\land p\not=1$이라는 결론을 얻는다.
이제 푸아송 근사를 논의하자. 푸아송 분포에서 $\lambda$는 상수이고, $n\to\infty$일 때, $p=\lambda/n$은 0에 수렴한다. 따라서 $p\to 0$인 경우에 푸아송 근사를 쓰는 것이 바람직하다.
그러므로 $0<p<1$일 때는 정규근사, $p\to0$일 때는 푸아송 근사를 쓰는 것이 적합하다. 만약 $p\to 1$이면 어떨까? 이때는 여사건을 이용한다. 성공확률이 1에 수렴하면 실패확률은 0으로 수렴하므로, 평균실패횟수를 모수 삼아 푸아송 분포를 구상하면 된다.
한편, 이항분포의 정규근사는 흔히 (1) $n \ge 30$; (2) $np \ge 5$; (3) $n(1-p) \ge 5$와 같은 조건이 붙는데, 이는 $n$이 충분히 크고, $p$가 0이나 1처럼 극단적이지 않은 값을 가지는 것을 표현한다.
