다음과 같이 정의된 연산을 함수 $f$와 $g$의 합성곱(Convolution; 卷积)이라고 하며 기호로는 $f\ast g$와 같이 나타낸다.
$$
(f\ast g)(t):=\int_{-\infty}^{\infty}f(x)g(t-x)\space dx
$$
함수의 합성곱 연산은 여러가지 의미를 가질 수 있으나, 수리통계학에서는 흔히 서로 독립인 두 확률변수의 합의 분포를 의미한다. 늘 그랬듯이 이산인 경우와 연속인 경우로 나누어 생각해보자.
#1. 이산분포의 합성곱
서로 독립인 두 이산확률변수 $X$와 $Y$의 분포를 각각 $f_X$와 $f_Y$로 놓으면, 새로운 변수 $Z=X+Y$의 분포 $f_Z=f_X \ast f_Y$이다.
$$
f_Z(z)=\sum_{x=0}^{z}f_X(x)f_Y(z-x)
$$
다음과 같이 $Z=X+Y$를 가정하고 $X$에 $0,1,\cdots,z$의 값을 부여할 때, $Y$는 $z,z-1,\cdots,0$의 값을 가질 것이다. 이것을 일반화 하면 $X=x$일 때 $Y=z-x$이다. 한편, $X\perp Y$이므로
$$P(X=x,Y=z-x)=P(X=x)P(Y=z-x)$$
이다. 서로 다른 $x=0,1,\cdots,z$에 대해 이렇게 확률의 곱셈을 계산한 뒤 그것들을 모두 합한 것이 곧 $P(Z=z)$가 된다.
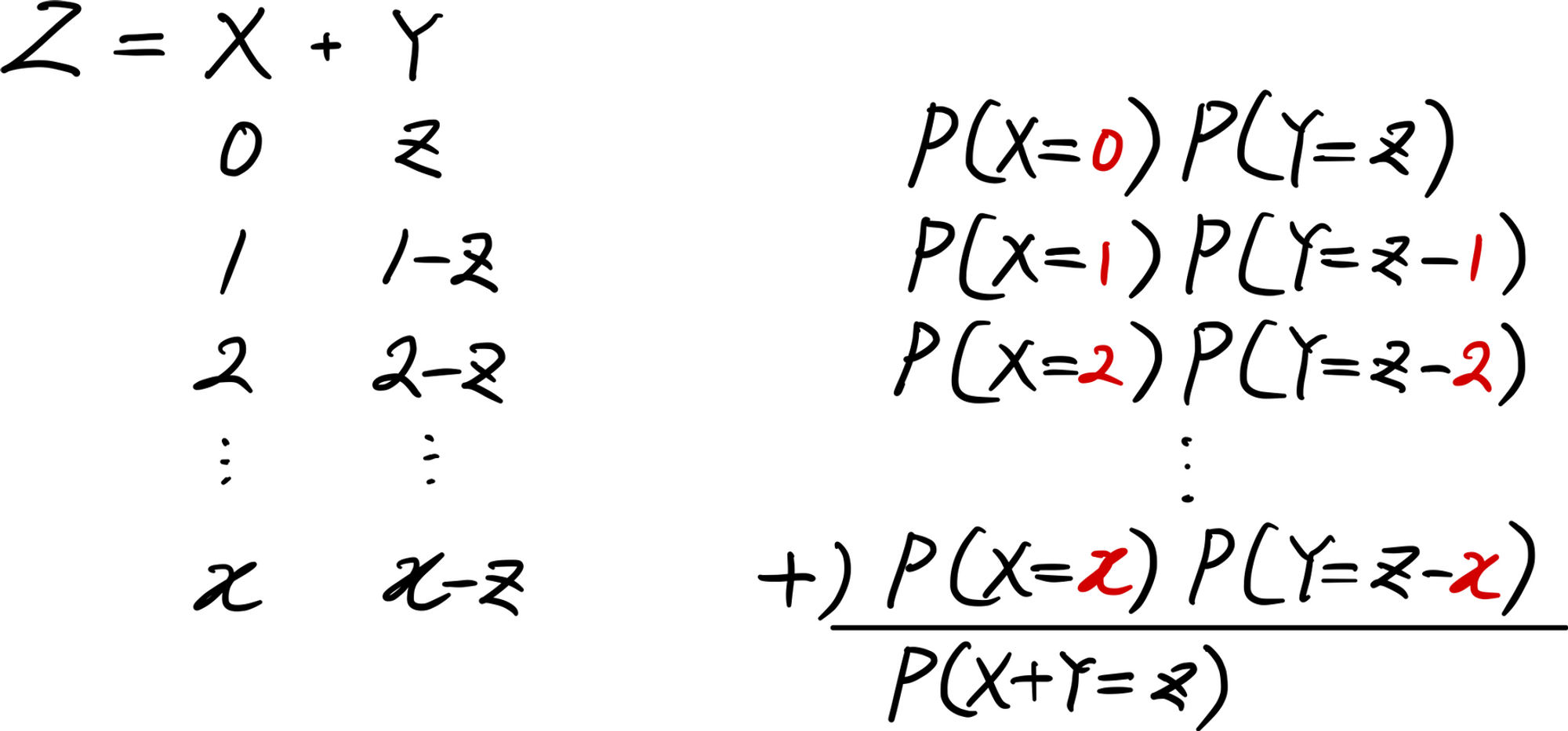
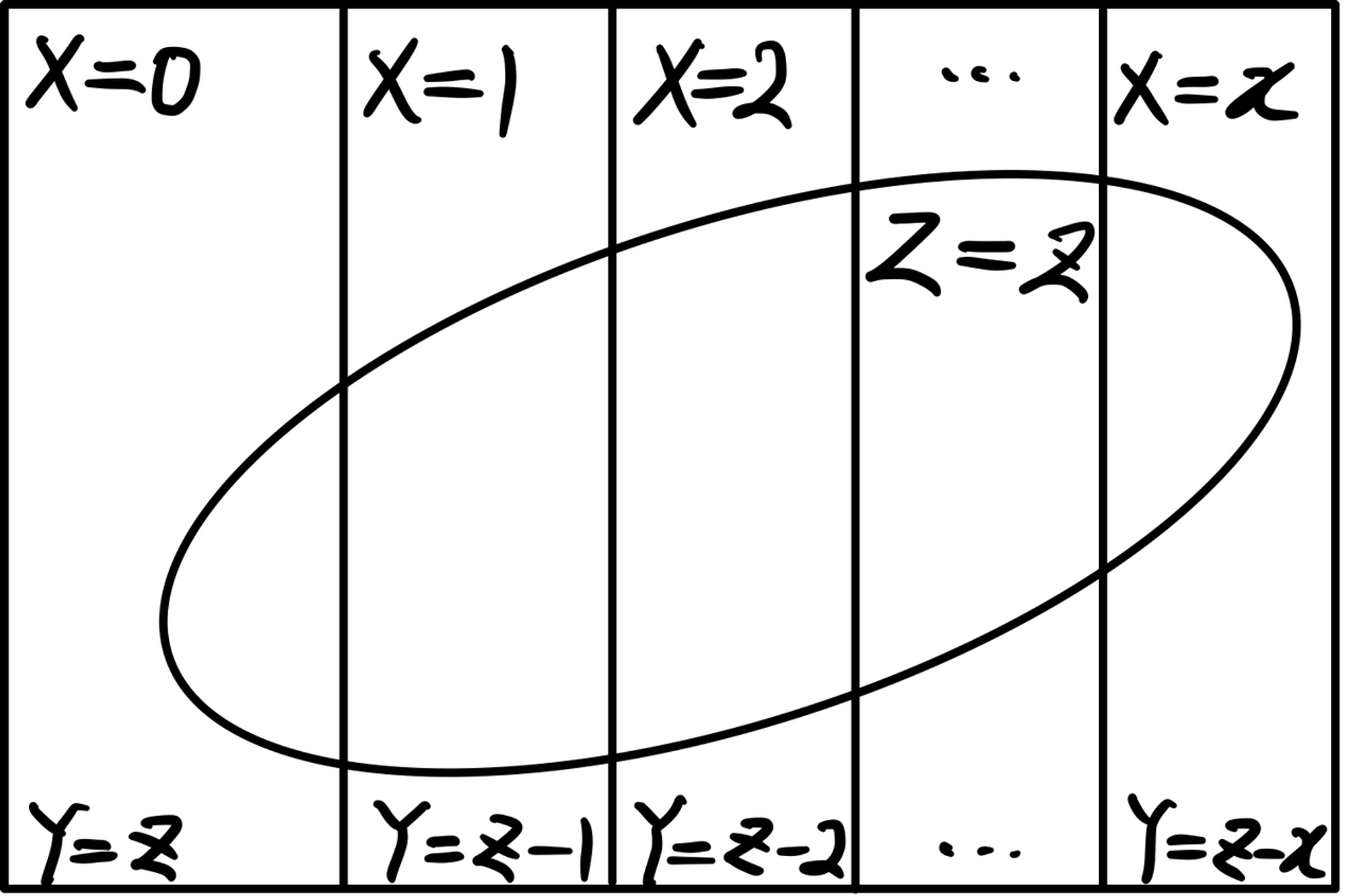
엄밀한 증명은 다음과 같이 사건 $\lbrace Z=z \rbrace$를 $\lbrace X+Y=z,X=x \rbrace,x=0,1,\cdots z$의 여러개의 사건으로 분할한 후, 전체확률의 법칙과 $X$, $Y$의 독립성을 이용한다.
$$
\begin{split}
P(Z=z)
&=\sum_{x=0}^{z}P(X=x)P(X+Y=z\mid X=x)(\because 전체확률의\enspace법칙)
\\
&=\sum_{x=0}^{z}P(X=x)P(Y=z-x\mid X=x)
\\
&=\sum_{x=0}^{z}P(X=x)P(Y=z-x)\space(\because X\perp Y)
\\
\therefore f_Z(z)&=\sum_{x=0}^{z}f_X(x)f_Y(z-x)
\end{split}
$$
$\space$
상기한 결과는 $X$에 $0,1,\cdots,z$의 값을 부여할 때 얻을 수 있다. 만약에 $X\in\mathbb{Z}$로 일반화한다면 다음과 같이 식이 변형된다.
$$
f_Z(z)=\sum_{x}f_X(x)f_Y(z-x),x\in\mathbb{Z}
$$
이렇게 변수의 범위가 일반화 될 때 비로소 ‘합성곱의 이산버전’이라고 할 수 있다. (일반적인 합성곱 연산의 정의에서, 적분구간이 음의 무한대에서 양의 무한대까지임을 주목하자.) 그러나 $X$는 이산확률변수이고, 이산확률변수는 보통 음이 아님을 가정한다는 사실을 감안하면(이것은 새로운 확률변수 $Z$도 마찬가지이다), $X$의 관측값을 0부터 $z$까지만 고려하는 것은 타당하다고 할 수 있다. 혹은 이산분포도 연속분포와 마찬가지로 지시함수를 도입하여 음인 구간의 확률을 모두 0으로 설정하면, 관측값의 구간을 정수 전체로 일반화 하더라도 결국에는 0부터 $z$까지 고려한 결과와 같아진다.
#2. 연속분포의 합성곱
이산분포의 합성곱에 합연산이 들어가므로 연속분포의 합성곱은 적분연산이 들어간다. 수학적 센스를 발휘하여 이산분포의 합성곱공식을 보고 아래와 같은 적분식을 바로 떠올릴 수도 있고, 일반적인 증명을 통해서 이해할 수도 있다.
$$
\begin{split}
(이산인\enspace 경우)\space &f_Z(z)=\sum_{x}f_X(x)f_Y(z-x),x\in\mathbb{Z}
\\
&\Downarrow
\\
(연속인\enspace 경우)\space &f_Z(z)=\int_{-\infty}^{\infty}f_X(x)f_Y(z-x)\space dx
\end{split}
$$
증명: 늘 써왔던 테크닉-먼저 누적분포구하고 미분해서 확률밀도 구하기.
$\space$
$$
F_Z(z)=P(X+Y\le z)=\iint\limits_{x+y\le z}f_{}(x,y)\space dxdy=\int_{-\infty}^{\infty}dx\int_{-\infty}^{z-x}f(x,y)\space dy
\\
\therefore f_Z(z)=\frac{d}{dz}F_Z(z)=\int_{-\infty}^{\infty}f(x,z-x)\space dx=\int_{-\infty}^{\infty}f_X(x)f_Y(z-x)\space dx
$$
$\space$
연속분포의 합성곱에 대해서도 적분구간 문제를 생각해보자. 흔히 다음과 같은 식을 두고 연속분포의 합성곱이라고 하는데, 이것은 상술한 연속분포의 관측값을 음이 아니도록 만든 것과 같다. 연속분포는 이산분포와 달리 적분구간을 지시함수를 통해 컨트롤 하는 것이 일반적이므로 적분구간이 $\mathbb{R}$이 아니더라도 당황할 필요는 없다.
$$
f_Z(z)=\int_{0}^{z}f_X(x)f_Y(z-x)\space dx
$$
#3. 응용
수리통계학에서 합성곱은 독립항등분포를 따르는 여러개의 확률변수를 통해 새로운 확률분포를 얻거나 어떤 확률분포를 여러개의 독립항등분포로 분해할 때 사용된다.
대표적인 예시가 바로 지난글에서 소개한 감마분포이다. 확률변수 $T \sim \Gamma(r,\lambda)$라고 가정하자. 즉, $f_{T}(t)=\frac{\lambda^r}{\Gamma(r)}t^{r-1}e^{-\lambda t}\mathbf{1}_
{[0,\infty)}(t)$이다. 이 수식의 의미들을 자연어로 ‘평균적으로 단위시간 내 $\lambda$회 정도 발생하는 사건이 실제로 $r$번 발생할 때까지 걸린 시간 $T$가 $t$근방의 값을 가질 확률이 $\int_{t-\epsilon}^{t+\epsilon} f_T(t)\space dt$로 주어진다’라고 해석할 수 있다. (감마분포 참조.)
한편, 감마분포와 지수분포의 관계는 $\Gamma(1,\lambda)=\mathrm{Exp}(\lambda)$으로 요약된다. 즉, 감마분포에서 $r=1$일 때가 곧 지수분포이다. 말하자면 지수분포는 감마분포의 특수한 형태라고 할 수 있다.
그렇다면 서로 독립인 확률변수 $T_i\sim\mathrm{Exp}(\lambda)(i=1,2)$을 가정할 때, $T=T_1+T_2\sim\Gamma(2,\lambda)$인가? 상술한 감마분포의 ‘자연어 해석’에 의해, 당연히 그래야만 한다. 어떤 사건이 ‘2번 발생할 때까지 걸린 시간’이라는 것은 어떤 사건이 ‘1번 발생할 때까지 걸린시간에 그 사건이 1번 더 발생할 때까지 걸린시간을 더한 것’이다. 전자가 $\Gamma(2,\lambda)$를 따른다면, 후자도 마땅히 $\Gamma(2,\lambda)$를 따라야 한다.
감마분포를 소개할 때는 이렇게 ‘의미적인 접근’을 하여 넘어갔지만, 이제 이 사실을 합성곱의 공식으로 도출해보자.
$$
\begin{split}
t\ge0,\space f_{T_1+T_2}(t)&=\int_{0}^{t}f_{T_1}(t_1)f_{T_2}(t-t_1)\space dt_1=\int_{0}^{t}\lambda e^{-\lambda t_1}\cdot\lambda e^{-\lambda(t-t_1)}\space dt_1
\\
&=\lambda^2e^{-\lambda t}\int_{0}^{t}dt_1=\lambda^2te^{-\lambda t}=\frac{\lambda^2}{\Gamma(2)}t^{2-1}e^{-\lambda t}
\\[5ex]
t<0,\space f_{T_1+T_2}(t)&=0
\\[5ex]
\therefore f_{T_1+T_2}(t)&=\frac{\lambda^2}{\Gamma(2)}t^{2-1}e^{-\lambda t}\mathbf{1}_
{[0,\infty)}(t)
\end{split}
$$
확실하게 $\Gamma(2,\lambda)$의 PDF를 얻었다. 이런 방식으로 합성곱 연산을 진행해나가다 보면, $\Gamma(3,\lambda)$는 지수분포 3개에 대해 합성곱 연산을 진행한 결과물이고, $\Gamma(r,\lambda)$란 사실 $\mathrm{Exp}(\lambda)$ $r$개를 합성곱한 것이라는 사실을 도출할 수 있다.

note1: $\Gamma(3,\lambda)$는 이미 $\mathrm{Exp}(\lambda)$ 2개가 합성곱된 결과물 $\Gamma(2,\lambda)$에 다시한번 $\mathrm{Exp}(\lambda)$를 합성곱함으로써 얻어진다. $\Gamma(4,\lambda)$는 $\Gamma(3,\lambda)\ast \mathrm{Exp}(\lambda)$로 구해도 좋고, $\Gamma(2,\lambda)\ast\Gamma(2,\lambda)$로 구해도 좋다.
note2: 합성곱 연산을 하다보면, 합성곱 연산이 교환법칙, 결합법칙을 만족한다는 사실이 직관적으로 받아들여진다. 합성곱 연산은 심지어 분배법칙까지 만족한다.
'확률론과 수리통계' 카테고리의 다른 글
| 확률변수의 최대, 최소의 분포 (0) | 2022.12.09 |
|---|---|
| 확률변수의 사칙연산의 분포 (0) | 2022.12.08 |
| Box-Muller 변환 (0) | 2022.11.30 |
| 야코비 행렬식 (0) | 2022.11.28 |
| 확률벡터의 변환 (0) | 2022.11.28 |


