이번 글에서는 확률변수 $X$와 $Y$의 결합분포 $f_{X,Y}$를 알고 있을 때 $f_{X+Y}$, $f_{X-Y}$, $f_{XY}$, $f_{X/Y}$를 구하는 법을 정리해보자. 여기서 얻은 결과들은 서로 독립인 확률변수 $X$와 $Y$의 분포 $f_X$와 $f_Y$를 알고 있을 때도 써먹을 수 있다(확률의 곱셈 참조).
#1. 합, 차의 분포
두 확률변수의 합의 분포는 다음과 같이 지난 글에서 설명한 합성곱을 떠올리면 된다.
$$
\begin{split}
(이산인\enspace 경우)\space &f_{X+Y}(z)=\sum_{x}f_X(x)f_Y(z-x),x\in\mathbb{Z}
\\
&\Downarrow
\\
(연속인\enspace 경우)\space &f_{X+Y}(z)=\int_{-\infty}^{\infty}f_X(x)f_Y(z-x)\space dx
\end{split}
$$
하지만 이것은 $X$와 $Y$가 독립일 때의 결과이다. (합성곱은 두 확률변수가 독립일 것을 요구한다.) 좀 더 일반적인 상황으로, $X$, $Y$의 독립 여부와 관계없이 다음이 성립한다. (증명은 합성곱 참조.)
$$
\begin{split}
(이산인\enspace 경우)\space &f_{X+Y}(z)=\sum_{x}f_{X,Y}(x,z-x),x\in\mathbb{Z}
\\
&\Downarrow
\\
(연속인\enspace 경우)\space &f_{X+Y}(z)=\int_{-\infty}^{\infty}f_{X,Y}(x,z-x)\space dx
\end{split}
$$
한편, 두 확률변수의 차의 분포는 다음과 같이 구한다. 합의 분포 공식에서 $z-x$를 뒤집어서 $x-z$로 만들면 된다.
$$
\begin{split}
(이산인\enspace 경우)\space &f_{X-Y}(z)=\sum_{x}f_{X,Y}(x,x-z),x\in\mathbb{Z}
\\
&\Downarrow
\\
(연속인\enspace 경우)\space &f_{X-Y}(z)=\int_{-\infty}^{\infty}f_{X,Y}(x,x-z)\space dx
\end{split}
$$
두 공식이 비슷한 생김새를 가진 이유는 무엇일까? 차의 분포 공식을 유도할 때, 합성곱 공식을 유도할 때와 비슷하게 유도해도 되고, ‘차’의 개념을 달리 생각하여 ‘마이너스를 더한 것’이라고 보아도 된다. 즉, $X-Y=X+(-Y)$임을 이용하자. 또, $X$와 $Y$가 독립이고, 분포 $f_X$와 $f_Y$를 알고 있다고 가정하자.
한편, 확률변수 $Y$의 분포가 $f_{Y}(y)$일 때, 새로운 확률변수 $-Y$의 분포는 $f_{Y}(-y)$이다. (확률변수의 변환 #3-1 참조.) 즉, $Y$의 관측값에 마이너스 기호를 붙이기만 하면 된다. 따라서 $z-x$에 마이너스 기호만 붙여서 $-(z-x)=x-z$로 만들기만 하면 되는 것이다.
#2. 곱, 몫의 분포
두 연속확률변수의 곱의 분포는 다음과 같이 구한다.
$$
f_{XY}(z)=\int_{-\infty}^{\infty}\frac{1}{\left\vert x\right\vert} f_{X,Y}\left(x,\frac{z}{x}\right)\space dx
$$
유도과정은 복잡한 편이다. 그러나 부호가 다를 때 절댓값 기호를 사용하여 하나로 합치는 테크닉은 익혀둘만 하다.

두 연속확률변수의 몫의 분포는 다음과 같이 구한다.
$$
f_{X/Y}(z)=\int_{-\infty}^{\infty}\left\vert y \right\vert f_{X,Y}\left(yz,y\right)\space dy
$$
곱의 분포 공식과 비슷하면서도 다르게 생겼다. 그러나 유도과정은 비슷하다.
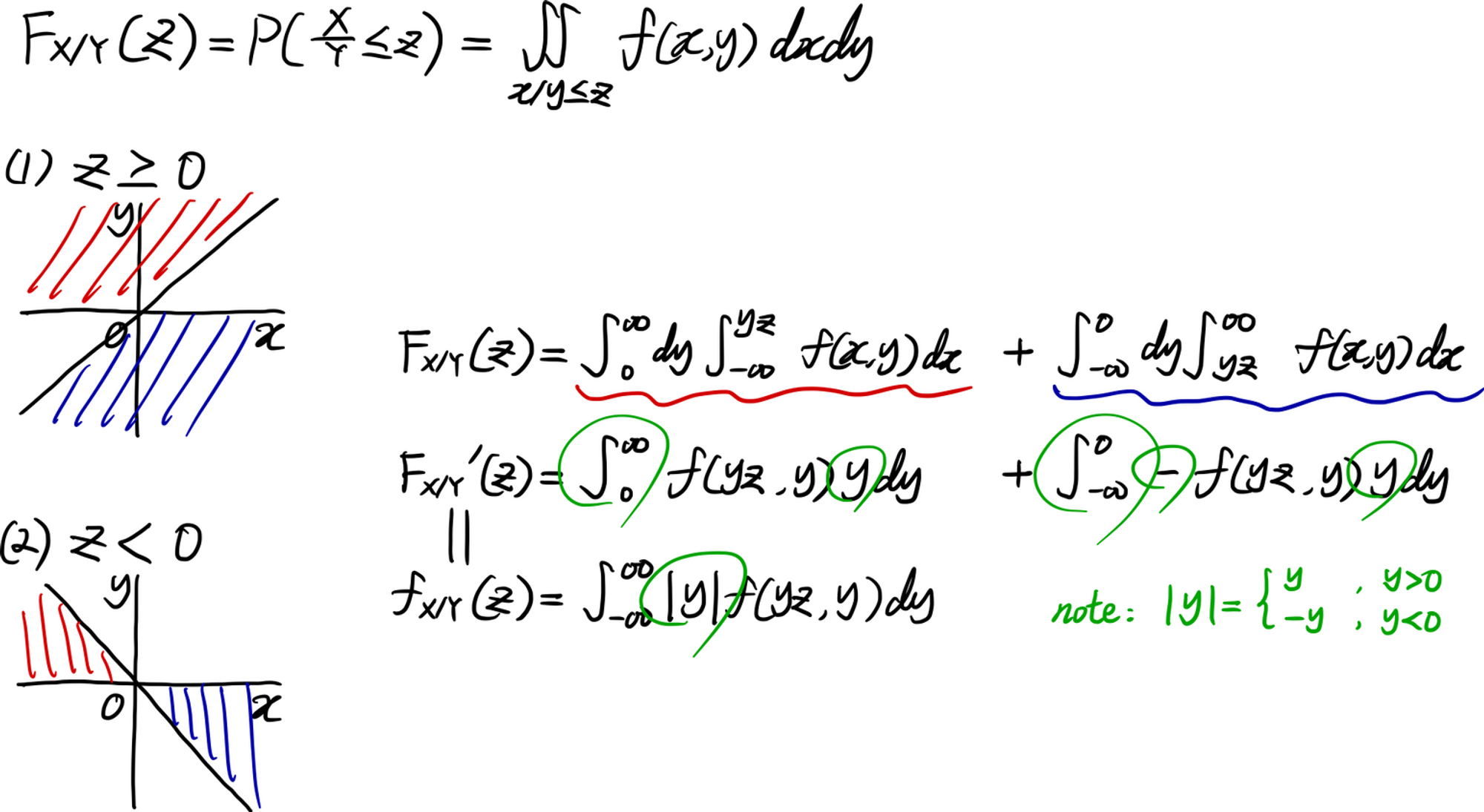
이산확률변수의 경우, 곱의 분포와 몫의 분포는 공식으로 해결하기 보다는 그때 그때 알맞게 계산하는 방식을 취한다.
'확률론과 수리통계' 카테고리의 다른 글
| 삼각분포 (0) | 2022.12.12 |
|---|---|
| 확률변수의 최대, 최소의 분포 (0) | 2022.12.09 |
| 합성곱 (0) | 2022.12.01 |
| Box-Muller 변환 (0) | 2022.11.30 |
| 야코비 행렬식 (0) | 2022.11.28 |


