확률변수의 수렴의 개념은 수리통계학의 중요한 두 이론인 큰 수의 법칙과 중심극한정리를 이해하는 데 핵심사항이다.
#0. 확률변수 수열
확률변수의 수렴을 논하기 전에, 반드시 짚고 가야하는 개념이 바로 ‘확률변수 수열’이다. ‘확률변수의 수렴’에서 ‘확률변수’는 여러개이기 때문이다.
영어로 하면 ‘Convergence of Random Variables’인데, ‘Variables’는 복수명사이다. 영어 원문 그대로의 뉘앙스를 살려 번역한다면 ‘확률변수들의 수렴’이겠지만, 그보다는 ‘확률변수의 수렴’이라고 번역하는게 깔끔하고 여기서 확률변수는 여러개임을 부연설명하는 것이 낫다.
확률변수가 여러개라는 것은 무슨 뜻일까? 동전던지기를 예로 들어보자. 동전던지기 시행의 결과는 베르누이 확률변수로 표현할 수 있다. 그러면 첫번째 결과를 $X_1=1$이라고 해보자. 이는 첫번째에서 앞면이 나왔다는 뜻이다. $X_2=0$은 두번째에서 뒷면이 나왔다는 뜻이다. $X_3=0$이면 세번째도 뒷면이라는 의미이고 이런식으로 $n$번째 시행의 결과는 $X_n=0\lor1$으로 나타낼 수 있다.
이제 앞의 3개의 확률변수의 평균(산술평균)을 구해보자.
$$ \frac{1}{3}\sum_{i=1}^{3}X_i=\frac{1}{3}(1+0+0)=\frac{1}{3} $$
그런데 동전던지기는 $\mathrm{Bern}(\frac{1}{2})$이므로 기댓값(평균)은 다음과 같다.
$$ \mathbb{E}(X)=1\cdot\frac{1}{2}+0\cdot\frac{1}{2}=\frac{1}{2} $$
지금 상태로는 평균과 기댓값이 다르다. 하지만 기댓값은 평균이라고도 불린다. 평균과 기댓값이 다르다는 것은 뭔가 모순적이지 않은가?
사실 ‘$\frac{1}{n}\sum_{i=1}^{n}X_i$은 $X_i$의 산술평균이고, $\mathbb{E}(X)$는 이론상 평균이다’라고 표현하면, 이와 같은 모순을 해결할 수 있다. 추후 소개할 큰 수의 법칙과 정리에 의해, $n\to\infty$일 때 이 둘이 같을 확률은 1이 된다. 즉 위와 같은 베르누이 시행에서 시행횟수 $n$이 충분히 많다면 산술평균 $\frac{1}{n}\sum_{i=1}^{n}X_i$는 기댓값 $\mathbb{E}(X)$에 수렴한다.
결국 기댓값은 수학적으로, 이론적으로 정해진 상수이다. 그리고 실제로 얻은 실험결과의 산술평균‘들’은 그 상수로 수렴하는 것이다.
확률변수는 상수로만 수렴하는게 아니라, 다른 확률변수로도 수렴할 수 있다. 균등분포를 따르는 확률변수들의 합이 정규분포로 수렴한다는 좋은 예시가 있다. (Irwin-Hall 분포 참조.) 이 식에서 $U_i$는 확률변수‘들’이고, $Z=\sum_{i=1}^{12}U_i-6$도 엄연한 확률변수이다.
$$ U_i\sim\mathrm{U}(0,1)\Rightarrow Z=\sum_{i=1}^{12}U_i-6\sim\mathrm{N}(0,1) $$
따라서 확률변수의 수렴 문제에서 확률변수가 여러개임을 강조하기 위해 ‘확률변수 수열 $\lbrace X_n \rbrace$의 기댓값을 $\mathbb{E}(X)$라고 하자.’와 같은 표현을 쓰기도 한다. 한국어처럼 복수명사가 보편적이지 않은 중국어도 마찬가지로 ‘设随机变量列 $\lbrace X_n\rbrace$ 的期望为 $\mathbb{E}(X)$。’와 같이 나타내므로 당황하지 말자.
‘확률변수의 수열’이라는 개념이 정립되면, 추후 등장할 ‘표본평균의 분포’같은 개념도 비슷하게 받아들일 수 있다. ‘아니 표본평균은 상수아니야? 거기서 왜 갑자기 분포가 나와?’같은 의문을 덜 가지게 되는 것이다.
#1. 확실히 수렴, 점별수렴
지난 글에서 소개한 ‘거의 확실히’라는 개념과 대조되는 ‘확실히’라는 개념을 차용한 수렴이다.
$$ \lim_{n\to\infty}X_n=X $$
이면, $X_n$은 $X$에 확실히 수렴(Sure Convergence; 必然收敛)한다.
확률변수가 $\Omega$에서 $\mathbb{R}$로 가는 함수라는 점을 고려하여
$$ \forall\omega\in\Omega:\lim_{n\to\infty}X_n(\omega)=X(\omega) $$
또는
$$ \lbrace\omega\in\Omega:\lim_{n\to\infty}X_n(\omega)=X(\omega)\rbrace=\Omega $$
으로 표현하며, 이때는 점별수렴(Pointwise Convergence; 逐点收敛)이라는 표현도 쓴다. 식을 보면 굉장히 강한 정도의 수렴임을 알 수 있는데, $\lim_{n\to\infty}X_n=X$가 필연사건 $\Omega$임을 어필하고 있다.
#2. 거의 확실히 수렴, 거의 어디서나 수렴
지난 글에서 소개한 ‘거의 확실히’라는 개념을 차용한 수렴이다.
$$ P\left(\lim_{n\to\infty}X_n=X\right)=1 $$
이면, $X_n$은 $X$에 거의 확실히 수렴(Almost Sure Convergence; 几乎必然收敛)한다.
식을 보면 확실히 수렴에서 한 발 양보한 것을 알 수있다. $\lim_{n\to\infty}X_n=X$가 필연사건 급은 아니지만 그래도 그 사건이 일어날 확률측도가 1임을 어필하고 있다.
이를 뒤집어서
$$ P\left(\lim_{n\to\infty}X_n\not=X\right)=0 $$
으로 표현할 수도 있다. 이렇게 표현하는 편이 지난 글에서 소개한 ‘어떤 사건이 거의 확실히 발생한다는 뜻은 그 사건이 발생하지 않을 확률측도가 0임을 뜻한다.’와 비슷하다.
note: ‘확실히 수렴’과 ‘거의 확실히 수렴’을 비교하면, 또 다시 ‘불가능사건(공집합)’과 ‘확률이 0(영집합)’의 차이, 그리고 ‘필연사건’과 ‘확률이 1’의 차이를 음미할 수 있다. ‘성공 가능성이 0%’라는 말을 들었을 때, 수학자는 ‘불가능하지는 않구나’라고 생각할 것이고, 만화에서 어떤 주인공이 ‘너는 100%의 확률로 죽어있다.’라는 대사를 날릴 때, 상대가 수학자라면 ‘내가 죽는다는게 필연사건은 아니구나’라고 안심할 것이다.
#3. 확률수렴
거의 확실히 수렴에서 한 발 더 양보해서
$$ \forall\epsilon>0:\lim_{n\to\infty}P(\vert X_n-X\vert<\epsilon)=1 $$
이면 $X_n$은 $X$에 확률수렴(Convergence in Probability; 依概率收敛)한다.
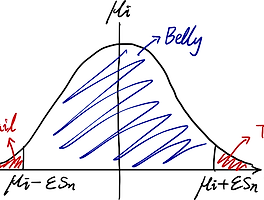
$\lim_{n\to\infty}X_n=X$라는 사건 대신 $\forall\epsilon>0:\vert X_n-X\vert<\epsilon$라는 사건의 확률이 1임을 어필하고 있다. 수리통계학에서 이 둘의 차이를 이해하는 것이 난관인데, 나는 다음과 같이 그림을 그려서 이해했다.

확실히 확률수렴의 기준이 더 널널하다. $\lim_{n\to\infty}X_n=X$라고 단언하지는 않지만, 그 둘의 차이는 상상할 수 있는 어떤 수보다 작다고, 아주 작다고 간접적으로 표현하고 있다.
#4. 분포수렴
분포수렴은 앞의 수렴들과는 달리 확률변수끼리 같아지거나 차이가 작아진다고 단언하지 않는다. 요구기준은 아주 널널한데, 확률변수끼리 값은 다르더라도 따르는 분포만 같으면 된다.
$$ \lim_{n\to\infty}P(X_n\le x)=P(X\le x) $$
이면 $X_n$은 $X$에 분포수렴(Convergence in Distribution; 依分布收敛)한다.
분포함수를 나타내는 $F$를 써서 다음과 같이 나타내기도 한다.
$$ \lim_{n\to\infty}F_n(x)=F(x) $$
#5. 수렴간 관계
이상의 4가지 수렴을 나타내는 기호들을 정리한다.
(1) 확실히 수렴: $\to$
(2) 거의 확실히 수렴: $\overset{\mathrm{a.s.}}{\to}$ 또는 $\to(\mathrm{a.s.})$
(3) 확률수렴: $\overset{p}{\to}$ 또는 $\to(p)$
(4) 분포수렴: $\overset{d}{\to}$ 또는 $\to(d)$
이 4가지의 수렴 사이의 관계를 그림으로 나타내면 다음과 같다.

우선, 일반적인 수렴의 강약에 의해 확실한 수렴부터 분포수렴까지 쭉 유도할 수 있다. 그리고 $X$가 상수라는 조건이 주어지면 분포수렴에서 확률수렴을 유도할 수 있고, 또 추가조건이 주어지면(수렴속도가 충분히 빠르면) 확률수렴에서 거의 확실한 수렴을 유도할 수 있다.
그리고 확률수렴에 대해 다음과 같은 정리도 있다.
$$ X_n\overset{p}{\to}X,Y_n\overset{p}{\to}Y\Rightarrow (X_n,Y_n)\overset{p}{\to}(X,Y) $$
비슷한 결론을 분포수렴에 대해서도 얻을 수 있는데, $Y$가 상수라는 조건이 붙는다. 분포수렴이 비교적 약한 정도의 수렴이라는 사실이 드러난다.
$$ X_n\overset{d}{\to}X,Y_n\overset{d}{\to}c\Rightarrow (X_n,Y_n)\overset{d}{\to}(X,c) $$