#1. 확률변수의 정의
이번 글에서는 수리통계의 꽃인 확률변수(Random Variable, RV; 随机变量)를 엄밀하게 정의해보자. 확률변수는 사건의 결과를 숫자로 나타낸 것이다.
예를 들어 동전을 3회 던지는 확률시행에서 앞면이 두 번 나오는 사건은 다음과 같다.
$$
\lbrace (H,H,T),(H,T,H),(T,H,H) \rbrace
$$
그렇다면 동전을 3회 던져 앞면이 두 번 나올 사건의 확률은 다음과 같을 것이다.
$$
P(\lbrace (H,H,T),(H,T,H),(T,H,H) \rbrace)
$$
이렇게 확률은 나타내면 매우 번거롭다. 동전을 던지는 횟수가 늘어날 수록, 더욱 복잡한 표기가 필요할 것이다. 심지어 ‘동전을 100회 던져 앞면이 두 번 이상 10번 미만 나올 확률’같은 복잡한 사건의 확률은 나타낼 여백이 부족하다. 또 그것을 기호로 나타냈다고 쳐도 그 기호가 무슨 뜻인지 알아보려면 $H$의 개수를 한참을 세고 있어야 한다.
이러한 문제를 해결하기 위해 확률변수가 도입된다. $i$번째 시행에 대해 확률변수 $X_i$를 설정하고, 동전을 던져서 앞면이 나오는 결과를 $X_i=1$, 뒷면이 나오는 결과를 $X_i=0$으로 표시하면, 동전을 100회 던져 앞면이 나오는 횟수는 $\sum_{i=1}^{100}X_i$이고, 위의 확률은 다음과 같이 부등식을 써서 나타낼 수 있다.
$$
P\left(2\le\sum_{i=1}^{100}X_i<10\right)
$$
물론 새로운 확률변수 $Y:=\sum_{i=1}^{100}X_i$를 도입해서 $P\left(2\le Y<10\right)$과 같이 나타내는 방법도 있을 것이다. 핵심은 확률변수는 복잡한 사건의 결과를 한 눈에 알아볼 수 있도록 숫자로 나타낸 것으로, 수리통계학의 기술과 이해를 매우 편리하게 한다는 데 있다.
그런데 ‘사건의 결과를 숫자로 나타낸다’라는 엄밀하지 않은 표현이 수학자들 마음에 들지 않았던 모양이다. 그래서 수학자들은 함수의 개념을 빌려 사건을 숫자에 대응시키는 행위를 엄밀하게 묘사했다. 이것이 바로 현대적인 확률변수의 정의이다. 지금은 이해가 안 가더라도 다음과 같은 문장을 기억하자:
“확률변수 $X$는 정의역이 $(\Omega,\mathcal{F})$, 공역이 $(\mathbb{R},\mathcal{B}(\mathbb{R}))$인 가측함수이다.”
#2.함수와 사상
우선 함수(Function; 函数)와 사상(Mapping; 映射)의 개념에 대해 복습하고 넘어가자.
함수 $f:X\to Y$를 생각하자(집합을 이용한 표기). 이 경우 $x\in X$에 대해, $x\mapsto f(x)=x^2$으로 나타낼 수도 있다(원소를 이용한 표기). 집합 $X$는 $f$의 정의역(Domain; 定义域), 집합 $Y$는 $f$의 공역(Codomain; 陪域), 그리고 $Y$의 부분집합 $f(X)$는 $f$의 치역(Range; 值域)이라고 한다.

note: $f(X)$에서 $X$는 집합이고, $f(X)$역시 집합이다. 집합 $f(X)$의 원소를 함수값 $f(x)$이라고 한다. $f(X)$에서 $X$가 집합임을 강조하기 위해서 $f[X]$와 같이 나타내기도 한다. 어떤 책에서는 사건 $A$가 발생할 확률을 $P(A)$가 아닌 $P[A]$라고 쓰기도 하는데 아마도 이런 관점을 반영하지 않았나 싶다.
함수는 결국 집합의 원소를 대응시키는 규칙이라고 할 수 있다. 그런데 이런 ‘대응 규칙’이 꼭 숫자와 숫자를 대응시킨다고 할 수는 없다. 프로그래밍 언어인 파이썬의 매서드를 생각해보자. ‘reverse()’는 괄호 안에 리스트를 넣으면 그 리스트 안 원소의 순서를 반전시킨 리스트를 반환한다. 따라서 리스트 자료를 또 다른 리스트 자료에 대응시키는 ‘함수’라고 볼 수 있다. ‘len()’는 괄호 안에 리스트를 넣으면 그 리스트의 원소의 개수를 반환하므로 리스트 자료를 정수에 대응시키는 ‘함수’라고 볼 수 있다.
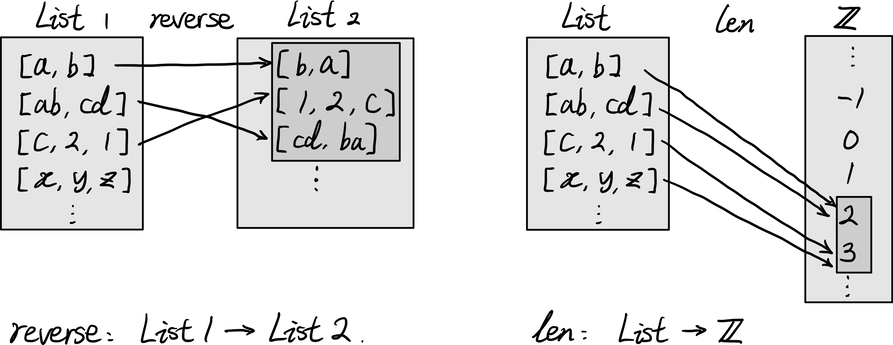
어떤 대상이 숫자인지 여부에 관계 없이 그것을 또 다른 대상에 대응시키는 규칙이 있으면 그것도 ‘함수’라고 할 만하다. 어떤 사람의 가치관이 자신을 1순위, 가족을 2순위, 친구를 3순위, 그 외 사람을 4순위에 놓는다면 그 사람의 가치관은 ‘사람’이라는 집합을 $\mathbb{Z}$에 대응시키는 ‘함수’이다.
이렇게 함수를 일반화 시킨 것을 사상이라고 한다. 다시 말해 함수는 숫자를 다루는 사상이며, 사상의 특수한 경우라고 볼 수 있다. 사상과 함수를 굳이 구분하지 않고 둘 다 함수라고 하며, 사상은 좀 더 일반화된 함수라고 보는 경우도 있다.
사상이라는 용어를 쓸 때는 치역 $f(X)$를 상(Image; 像)이라고 한다. 상은 다음과 같이 정의되는 공역의 부분집합이다.
$$
f(X):=\lbrace f(x):x\in X\rbrace
$$
상이 있으면 그것을 거꾸로 뒤집은 원상(Preimage; 原像)이 있다. 원상은 $f^{-1}$처럼 나타내며, 다음과 같이 정의되는 집합이다. 원상을 역상(Inverse Image; 逆像)이라고도 한다. 공역 $Y$의 부분집합 $A$의 원상 $f^{-1}(A)$는 다음과 같이 정의되는 $X$의 부분집합이다.
$$
f^{-1}(A):=\lbrace x\in X: f(x)\in A\rbrace
$$
#3. 가측함수와 가측사상
이제 함수와 사상의 언어로 확률변수를 표현해보자. 확률변수의 목적은 ‘사건의 결과’를 ‘숫자’에 대응시키는 것이다. 사건의 결과를 모아놓은 집합은 표본공간 $\Omega$이고, 숫자를 모아놓은 집합은 실수의 집합 $\mathbb{R}$이다. 따라서 확률변수 $X$는 다음과 같이 정의되는 사상이다.
$$
X:\Omega\to\mathbb{R}
$$
그런데 확률론에서 $\Omega$는 보렐 필드 $\mathcal{F}$와 확률측도 $P$를 갖추었다. 즉, $\Omega$를 측정하는 것이 가능하도록 열심히 확률공간 $(\Omega,\mathcal{F},P)$를 구축해놓은 것이다. 확률공간을 구축한 노력이 헛되지 않도록, 공역인 $\mathbb{R}$도 가측이기를 원한다. 따라서 $\mathbb{R}$도 측정이 가능하도록 $\mathbb{R}$ 위의 보렐-시그마 대수 $\mathcal{B}(\mathbb{R})$을 부여한다. ($\Omega$ 위의 보렐-시그마 대수를 보렐 필드 $\mathcal{F}$로 나타냈음을 상기하자.) 확률변수는 이렇게 새롭게 구축한 가측공간 $(\mathbb{R},\mathcal{B}(\mathbb{R}))$을 공역으로 삼는다.
한편, 상 $X(\Omega)$와 원상 $X^{-1}(\mathbb{R})$은 다음과 같이 나타낼 수 있다.
$$
\begin{split}
X(\Omega)&:=\lbrace X(\omega):\omega \in \Omega \rbrace
\\
X^{-1}(\mathbb{R})&:=\lbrace\omega\in\Omega:X(\omega)\in \mathbb{R}\rbrace
\end{split}
$$
다시 말해 확률변수 값의 원상은 표본공간의 부분집합, 즉 사건이다.
그런데 새로운 가측공간 $(\mathbb{R},\mathcal{B}(\mathbb{R}))$은 새로운 시그마 대수 $\mathcal{B}(\mathbb{R})$을 갖추고 있다. 이 새로운 시그마 대수의 원상도 원래 표본공간의 시그마 대수의 부분집합인가? 모든 사상이 그렇다는 보장은 없지만, 확률변수라는 것이 잘 작동하려면, 그리고 앞선 노력이 헛되지 않으려면 그래야 한다. 이것을 만족하는 사상을 가측사상(Measurable Mapping; 可测映射)이라고 한다. 확률변수는 일종의 가측사상인 것이다.
가측사상의 일반적인 정의는 다음과 같다. 공역 위의 시그마대수의 원상이 정의역 위의 시그마대수에 포함되어야 한다는 것을 요구하고 있다.
$\space$
가측공간 $(X,\mathcal{F})$와 $(Y,\mathcal{G})$에 대해, 사상 $f:X\to Y$가 $f^{-1}(\mathcal{G})\subseteq\mathcal{F}$를 만족하면 $f$는 $(X,\mathcal{F})$에서 $(Y,\mathcal{G})$로 가는 가측사상이라고 하고, $f \in \mathcal{F}$와 같이 나타낸다. $f^{-1}(\mathcal{G})$는 $\mathcal{F}$의 부분집합이므로 역시 시그마대수이다. 그러므로 $f$에 의해 생성된 시그마대수라고 하며, $\sigma(f)$와 같이 나타낸다.
$\space$
함수와 사상의 관계를 고려했을 때 확률변수 $X:(\Omega,\mathcal{F})\to(\mathbb{R},\mathcal{B}(\mathbb{R}))$는 가측함수라고 불려야 정확하다. 숫자를 다루기 때문이다. 확률변수가 가측함수이므로 $X^{-1}(\mathcal{B}(\mathbb{R}))$은 보렐 필드 $\mathcal{F}$의 부분집합, 즉 사건의 집합이며, 가측인 것을 모아놓은 것이다. 이를 두고 원상이 가측성을 보존한다고 표현한다.
확률변수가 가측함수여야 한다는 조건은 이렇게도 이해할 수 있다. $\mathcal{B}(\mathbb{R})$은 온갖 실수 구간을 모아놓은 집합이다. 즉, $[0,1]$, $[5,10)$, $\cdots$ 등이 $\mathcal{B}(\mathbb{R})$에 원소로서 속해있다. 확률변수는 표본공간을 실수 집합에 대응시킨 것이다. 이 과정에서 자연스럽게 표본공간 $\Omega$ 위의 시그마 대수인 보렐 필드 $\mathcal{F}$, 즉 사건의 모임이 실수 집합위의 보렐-시그마 대수인 실수 구간의 모임 $\mathcal{B}(\mathbb{R})$에 대응된다. 실수 집합의 역상 $X^{-1}(\mathbb{R})$은 표본공간의 부분집합이므로, 실수 구간의 집합의 역상 $X^{-1}(\mathcal{B}(\mathbb{R}))$은 보렐 필드의 부분집합이어야 맞다. 다시 말해 실수 구간 $[0,1]$, $[5,10)$, $\cdots$ 등은 각자 해당되는 사건이 존재한다는 뜻이다.
요약하자면, “그래서 확률변수가 뭔데?”라는 질문을 받았을 때, 상대가 일반인이라면 “확률변수는 사건의 결과를 숫자로 나타낸 거야.”라고 대답하고, 상대가 수학자라면 다음과 같이 대답하자.
“확률변수 $X$는 정의역이 $(\Omega,\mathcal{F})$, 공역이 $(\mathbb{R},\mathcal{B}(\mathbb{R}))$인 가측함수이다.”
#4. 확률변수로 나타낸 확률측도
확률변수가 $(\Omega,\mathcal{F})\to(\mathbb{R},\mathcal{B}(\mathbb{R}))$처럼 정의되는 사상이듯이, 확률측도, 즉 흔히 말하는 확률 역시 $P:(\Omega,\mathcal{F})\to[0,1]$인 사상으로 볼 수 있다. 마찬가지로 $(\mathbb{R},\mathcal{B}(\mathbb{R}))$에서 $[0,1]$로 가는 사상 $P_X$를 $P_X:(\mathbb{R},\mathcal{B}(\mathbb{R}))\to[0,1]$와 같이 정의할 수 있다.
예를 들어 동전 2개를 던져서 앞면이 1개만 나올 확률은 다음과 같이 나타낼 수 있다. 여기서 $X$는 앞면의 개수이다.
$$
P(\lbrace (H,T),(T,H)\rbrace)=P_X(\lbrace 1\rbrace)=0.5
$$
그런데 $\lbrace (H,T) \rbrace$와 같은 사건은 확률변수로 나타낼 수 없다. $\lbrace X:X=1 \rbrace$과 같이 나타낼 수는 없다. $\lbrace X:X=1 \rbrace$에 해당하는 사건은 $\lbrace (H,T) \rbrace$가 아니라 $\lbrace (H,T),(T,H)\rbrace$이다. 이 경우는 다음과 같이 $P$를 써서 $(\mathbb{R},\mathcal{B}(\mathbb{R}))$을 거치지 않고 바로 $[0,1]$로 보내면 된다.
$$
P(\lbrace (H,T)\rbrace)=0.25
$$
즉, 확률변수의 이용은 선택사항인 것이다. 보렐필드 $\mathcal{F}$에서 $\mathbb{R}$ 위의 보렐-시그마 대수 $\mathcal{B}(\mathbb{R})$을 거쳐 $[0,1]$로 갈 수도 있지만, 보렐필드에서 바로 $[0,1]$으로 가는 것도 가능하다.

note: $\mathbb{R}$ 위의 보렐-시그마 대수 $\mathcal{B}(\mathbb{R})$의 원소를 보자. 전부 ‘점’ 또는 ‘점의 모임’이다. 그럼에도 불구하고 이산확률변수의 공역에는 르베그-시그마대수라는 표현을 쓰지 않았다. 유한개의 점의 모임에서 점을 1개 고를 확률측도는 0이 아니기 때문이다. 점 $n$개 중 1개를 고를 확률은 $1/n$이고 0이 아니다. 하지만 어떤 선분($n\to\infty$) 위에서 점 1개를 고를 확률은 0이다. 이를 $\mathbb{R}$에서의 르베그 외측도가 0이라고 표현하기로 했다. 고전적확률과 기하학적확률의 차이를 여기서도 확인할 수 있다.
한편, $\lbrace X:X=1 \rbrace$는 확률변수를 이용하여 나타낸 사건이므로 보렐 필드 $\mathcal{F}$의 원소이다. 따라서 $P_X$ 대신에 $P$를 사용해서 $P_{X}(\lbrace1\rbrace)=P(\lbrace X:X=1 \rbrace)$처럼 나타낼 수 있다. 이 표기가 비교적 번거로우므로 간단히 $P(\lbrace X:X=1 \rbrace)=P(X=1)$처럼 쓴다. 물론 $P(\lbrace X:0<X\le1 \rbrace)=P(0<X\le 1)$과 같은 표기도 가능하다.
원상 $X^{-1}(\mathbb{R})$, $X^{-1}(\mathcal{B}(\mathbb{R}))$은 사건이다. 따라서 $P$와 $X^{-1}$의 합성 $P\circ X^{-1}$는 어떤 사건의 확률을 나타내고, 이것을 확률변수 $X$의 확률분포(Probability Distribution; 概率分布), 간단히 분포(Distribution; 分布)라고 부른다. $P\circ X^{-1}=P_X$임을 쉽게 알 수 있다.
확률분포는 일종의 합성함수이므로 $f_X$, $F_X$와 같이 나타내기도 한다. 이것은 각각 확률밀도(질량)함수와 누적분포함수의 기호로 사용된다. 확률밀도(질량)함수와 누적분포함수가 확률분포를 나타내는 한 방법임을 상기하자.


