#1. 결합분포
실제 응용 측면에서는 여러 확률변수를 동시에 다뤄야 하는 경우가 생긴다. 다변수함수가 있듯이, 다차원 확률변수의 분포함수 역시 있을 것이다. 다변수함수 $f(x,y)$는 $x$와 $y$의 함수로 볼 수도 있지만, $(x,y)$라는 이차원 벡터의 함수로 볼 수도 있다. 마찬가지로 $X$와 $Y$의 확률분포 역시 $(X,Y)$라는 이차원 확률벡터의 함수로 볼 수 있다. 일반적인 $n$차원 확률벡터와 그 분포의 정의는 다음과 같다.
$\space$
$X_i(i=1,2,\cdots,n)$는 같은 확률공간 $(\Omega,\mathcal{F},P)$ 위에서 정의된 $n$개의 확률변수들이다. 이것들을 한데 모은 순서쌍 $\mathbf{X}:=(X_1,X_2,\cdots,X_n)$을 $n$차원 확률벡터($n$-Dimensional Random Vector; $n$维随机向量)라고 한다.
함수 $F_{\mathbf{X}}(x_1,x_2,\cdots,x_n):=P(X_1 \le x_1,X_2\le x_2,\cdots, X_n\le x_n)$을 확률벡터 $\mathbf{X}$의 누적분포함수라고 하거나, 확률변수 $X_i(i=1,2,\cdots,n)$의 결합누적분포함수(Joint CDF; 联合累积分布函数)라고 한다.
$\mathbf{x}:=(x_1,x_2,\cdots,x_n)$으로 정의하여 $F_{\mathbf{X}}(\mathbf{x})$와 같이 나타내기도 한다.
$\space$
note: $P(X_1 \le x_1,X_2\le x_2,\cdots, X_n\le x_n)$에서 ‘,’는 교집합($\cap$), 여러 사건의 동시발생의 의미를 갖는다. 원래는 $P(\lbrace X_1: X_1 \le x_1 \rbrace\cap\lbrace X_2: X_2\le x_2 \rbrace\cap\cdots\cap\lbrace X_n: X_n\le x_n \rbrace)$와 같이 집합의 언어로 표현해야 맞지만 표기의 간편함을 위해서 이렇게 쓰기도 한다.
연속확률변수에 대해서는 다음이 성립한다. $f_{\mathbf{X}}$는 결합확률밀도함수(Joint PDF; 联合概率密度函数)이다.
$$
F_{\mathbf{X}}(\mathbf{x})=\int_{-\infty}^{x_1}\int_{-\infty}^{x_2}\cdots\int_{-\infty}^{x_n} f_{\mathbf{X}}(x_1,x_2,\cdots,x_n)\space \mathrm{d}x_1\mathrm{d}x_2\cdots\mathrm{d}x_n
$$
비슷하게 이산확률변수에 대해 결합확률질량함수(Joint PMF; 联合概率质量函数)도 생각해볼 수 있다. 결합확률밀도함수, 결합확률질량함수, 결합누적분포함수를 통틀어 결합분포(Joint Distribution; 联合分布)라고 한다. 결합밀도, 결합질량, 결합확률밀도, 결합확률질량 등 여러 축약된 용어가 있으나 핵심은 ‘결합’으로, 이 용어가 빠지는 경우는 없다. ‘결합’은 여러 확률변수를 동시에 고려했음을 의미한다.
#2. 주변분포
$n$차원 확률분포는 특히 $n=2$인 경우가 자주 쓰인다. 확률벡터 $(X,Y)$의 분포를 $f_{(X,Y)}(x,y)$, 간단히 $f(x,y)$로 나타낸다. 이때 관심있는 변수 하나만의 분포는 $f_X(x)$, $f_Y(y)$와 같이 나타내며, 각각 $X$와 $Y$의 주변분포(Marginal Distribution; 边缘分布)라고 한다. 주변분포 역시 결합분포처럼 여러 용어가 있지만 아무튼 핵심 키워드는 ‘주변’이다. ‘주변’은 여러 확률변수 중 하나만 고려했음을 의미한다.
주변분포와 비슷하게, 여러 변수 중 하나만 고려하고 나머지는 무시하는 수학의 표현방법을 배운 적이 있다. 바로 편미분과 편적분이다. 연속확률벡터의 경우 다음이 성립한다.
$$
f_X(x)=\int_{-\infty}^{\infty}f(x,y)\space\mathrm{d}y
\\
f_Y(y)=\int_{-\infty}^{\infty}f(x,y)\space\mathrm{d}x
\\
f(x,y)=\frac{\partial^2}{\partial x\partial y}F(x,y)
$$
이산확률벡터에 대해서는 다음이 성립한다.
$$
f_X(x)=\sum_{y}f(x,y)
\\
f_Y(y)=\sum_{x}f(x,y)
$$
이산인 경우를 먼저 이해하고 연속인 경우를 이해하는 편이 좋다. 이산확률변수의 주변분포의 식을 관찰해보면, $f_X(x)$는 $Y$의 값이 무엇이든 가리지 않고 $P(X=x)$인 확률을 모두 더한 것이다. 예를 들어 $X\in\lbrace0,1\rbrace$, $Y\in\lbrace0,1,2\rbrace$일 때 $P(X=1)$을 구한다고 해보자.
$$
P(X=1)=P(X=1,Y=0)+P(X=1,Y=1)+P(X=1,Y=2)
$$
이것이 가능한 이유는 $\Omega=\left(\sum_{y=0}^{2}\lbrace Y=y\rbrace\right)$처럼 표본공간이 분할되며, 다음이 성립하기 때문이다. (베이즈 정리 참조.)
$$
\lbrace X=1\rbrace=\lbrace X=1\rbrace\Omega=\lbrace X=1\rbrace\left(\sum_{y=0}^{2}\lbrace Y=y\rbrace\right)=\sum_{y=0}^{2}\lbrace X=1\rbrace\lbrace Y=y\rbrace
$$

$P$ 대신 $f_X$를 써서 나타내면(PMF의 형태) 위의 식처럼 나온다.
$$
f_X(1)=\sum_{y=0}^2 f(1,y)=f(1,0)+f(1,1)+f(1,2)
$$
이산적인 상황에서 ‘모두 더한다’는 것은 연속적인 상황에서는 ‘적분’으로 표현된다. $X\in[0,1]$, $Y\in[0,2]$일 때 $f_X(1)=\int_{0}^{2}f(1,y)\space\mathrm{d}y$와 같이 구할 수 있다.
#3. 조건부분포
조건부 확률의 정의에 의해 다음이 성립한다.
$$
P(X\le x\mid Y=y):=\frac{P(X\le x,Y=y)}{P(Y=y)}
$$
이것은 $Y=y$라는 조건 하의 $X$의 조건부분포(Contitional Distribution; 条件分布)이다. 조건부분포도 조건부확률분포, 조건부확률질량, 조건부확률밀도 등 여러 명칭이 있지만 핵심 키워드는 ‘조건부’이다.
사건의 독립과 비슷하게 확률변수의 독립도 정의할 수 있다. 예를 들어 두 확률변수 $X$와 $Y$가 독립이라는 것은 다음이 성립함을 뜻한다.
$$
P(X\le x,Y\le y)=P(X\le x)P(Y \le y)
$$
이 표현을 확률밀도와 질량의 표현으로 옮기면 다음과 같다.
$$
f(x,y)=f_X(x)f_Y(y)
$$
다시 말해 두 확률변수가 독립이면 그 확률변수들의 결합분포를 주변분포의 곱으로 나타낼 수 있다. 이와 비슷하게 여러 확률변수의 독립도 생각해 볼 수 있다. (사건의 독립 참조.)
#4. 예시를 통한 이해
빨간공 3개와 파란공 4개가 들어있는 항아리에서 순차적으로 임의의 공 1개씩을 꺼내는 시행을 2회 반복하는 폴리아 항아리모형을 생각해보자. 첫번째 확률시행의 결과를 나타내는 베르누이 확률변수를 다음과 같이 정의한다.
$$
X:=
\begin{cases}
1, & \mathrm{빨간공}
\\
0, & \mathrm{파란공}
\end{cases}
$$
두번째 확률시행의 결과를 나타내는 확률변수는 같은 방식으로 $Y$로 정하자.
이제 $X$와 $Y$의 결합분포를 구해보자. 결합분포는 다음과 같이 표로 나타낸다. (표는 함수를 나타내는 아주 좋은 방법이다.) 폴리아 항아리 모형에서는 공을 꺼냈다가 도로 항아리에 집어넣는 복원추출과 그렇지 않는 비복원추출이 구분된다. 복원추출은 매 확률시행의 독립을 보장하는 반면, 비복원추출은 그렇지 못하다. (고전적 확률 참조.) 이 점을 감안하여 두 가지 경우로 나누어 $f(x,y)$를 구해보자.

이 표를 유심히 관찰하면 매우 많은 것들을 알 수 있다.
(1) 주변분포 $f_X(x)$, $f_Y(y)$는 문자 그대로 표의 ‘주변’에 위치함을 알 수 있다. 조건분포는 어떨까? 베이즈 정리를 이용하여 진양성률을 구하는 방법과 비슷하다. 머릿속에 이미지를 떠올려서 기억해보자.
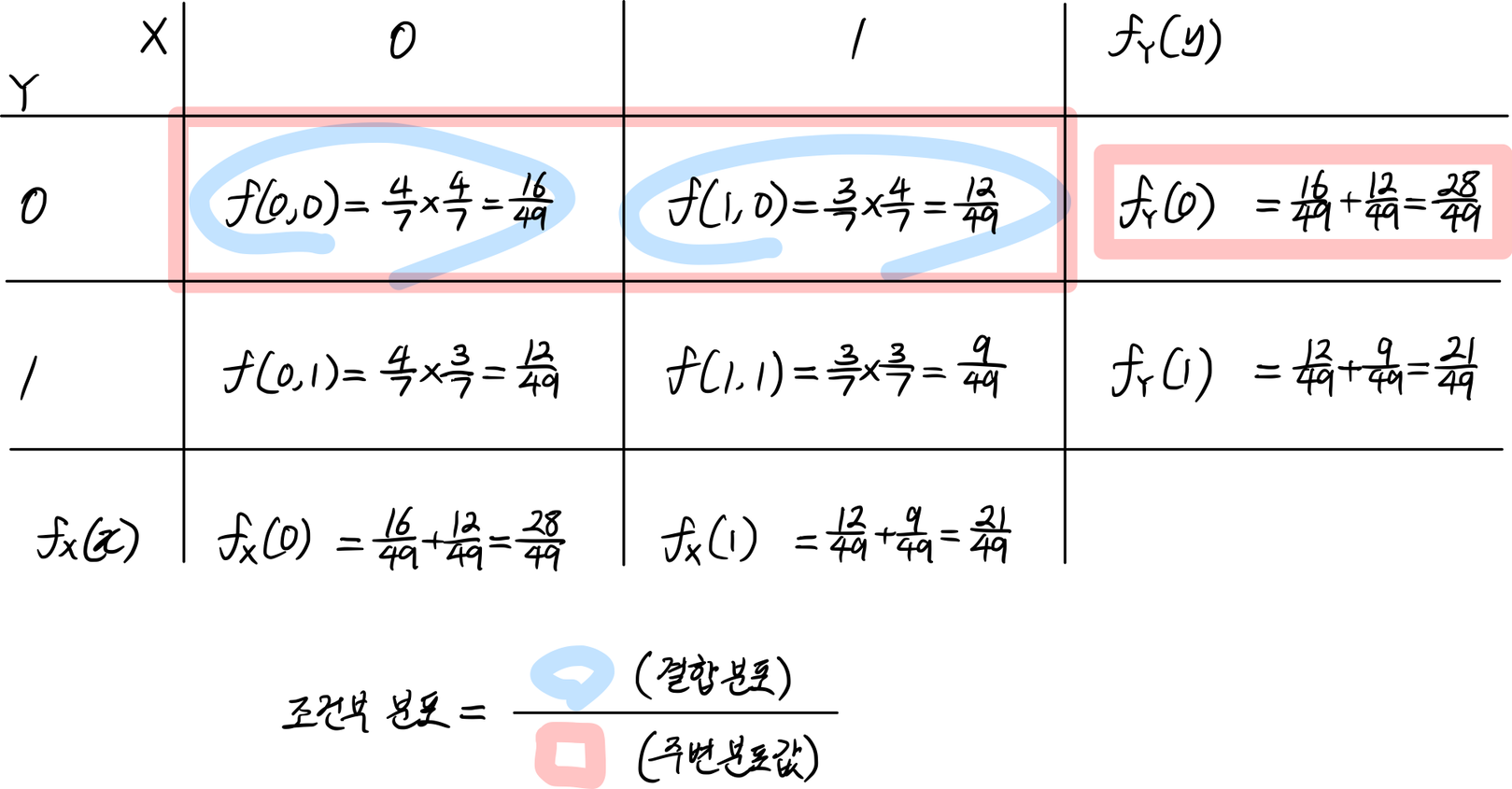
예를 들어 복원추출에서 $Y=0$이라는 조건 하의 $X$의 분포 $f_{X\mid Y}(x\mid 0)=P(X=x\mid Y=0)$는 다음과 같이 구한다.
$$
f_{X\mid Y}(0\mid 0)=\frac{f(0,0)}{f_Y(0)}=\frac{16/49}{28/49}=\frac{16}{28}
$$
$$
f_{X\mid Y}(1\mid 0)=\frac{f(1,0)}{f_Y(0)}=\frac{12/49}{28/49}=\frac{12}{28}
$$
이 결과는 조건부분포=결합분포/주변분포값으로 기억하면 된다. 분모는 주변분포가 아니라 주변분포 ‘값’이다. 즉, 상수인 것이다. 이 사실은 베이즈 추론을 이해할 때 핵심 사항이다. 베이즈 추론에서는 분모를 ‘증거’라고 하며 실제 응용에서는 상수취급 한다. 즉, 다음과 같이 비례기호를 써서 조건부분포와 결합분포의 관계를 나타낼 수 있다.
$$
조건부분포\propto결합분포
$$
조건부분포는 사후확률, 결합분포는 가능도와 사전확률의 곱으로 나타낼 수 있다. 따라서 다음과 같은 베이즈 추론의 식을 얻는다. (구체적인 베이즈 추론의 예시는 ‘베타분포의 응용’ 참조.)
$$
사후확률\propto가능도\times사전확률
$$
(2) 한편, $f_{X\mid Y}(0\mid 0)+f_{X\mid Y}(1\mid 0)=1$임을 알 수 있다. 이 사실은 조건부 확률은 주어진 조건을 새로운 ‘표본공간’(예시에서는 사건 $\lbrace Y:Y=0 \rbrace$)으로 삼는다는 사실과 일맥상통한다. 물론 확률측도 $P(\lbrace Y:Y=0 \rbrace)=28/49\not=1$이므로 진정한 표본공간은 아니다. 조건부 확률 참조.) 조건 분포 뿐만 아니라 어떤 분포이든지 모든 확률을 더하면 1이다. 콜모고로프 공리에서 표본공간의 확률측도를 1로 정했기 때문이다. (확률공간 참조.)
(3) 복원추출과 비복원추출의 주변분포가 같지만 각 결합분포는 다르다는 사실을 알 수 있다. 이를 통해 결합분포는 주변분포를 결정할 수 있지만, 주변분포는 결합분포를 결정할 수 없음을 알 수 있다. 예를 들어 $f_X(x)$와 $f_Y(y)$를 알아냈다고 해서 $f(x,y)=f_X(x)f_Y(y)$라고 쉽게 단정할 수 없다는 것이다. 이것이 성립하려면 $X\perp Y$라는 전제가 필요하다. 복원추출의 경우 이 전제가 깔려있지만 비복원추출의 경우 그렇지 않다는 사실도 확인 가능하다.

