Union-Find Algorithm

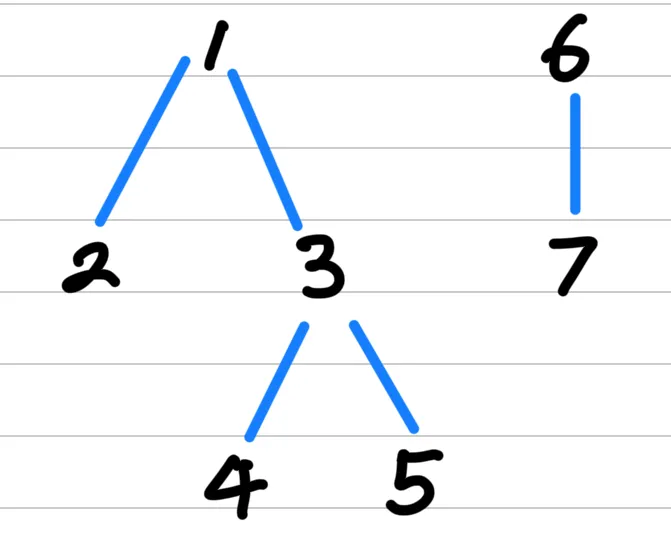
Find Root

This tree graph can be described by a parent table.

• parent = [0, 1, 1, 1, 3, 3, 6, 6], representing the parent node for each node. (including node 0, although it is not used.)
• parent[1] = 1, parent[6] = 6. They are roots of the other nodes, since their parents are themselves.
• parent[2] = parent[3] = 1, parent[4] = parent[5] = 3, parent[7] = 6.

The root of each node can be found using the parent table.

• If parent[i] = i, then the root of i is i itself.
• If parent[i] ≠ i, then we should find the root of parent[i], while parent[i] = i.
• For example, the root of node 5 can be found by following process:
  • Since parent[5] = 3 ≠ 5, find the root of parent[5] = 3.
  • Since parent[3] = 1 ≠ 3, find the root of parent[3] = 1.
  • Since parent[1] = 1, the root of node 5 is node 1.
• Python code for this process:

parent = [0, 1, 1, 1, 3, 3, 6, 6]

def find_root(x):
    if parent[x] != x:
        parent[x] = find_root(parent[x])
    return parent[x]

print(find_root(5))

Union-Find

When combining union and find, all the roots in the graph can be detected.

parent = [0, 1, 2, 3, 4, 5, 6, 7]
edges = [(1, 2), (1, 3), (3, 4), (3, 5), (6, 7)]

def find_root(x):
    if parent[x] != x:
        parent[x] = find_root(parent[x])
    return parent[x]

def union(x, y):
    root_x = find_root(x)
    root_y = find_root(y)
    if root_x != root_y:
        parent[root_y] = root_x

for edge in edges:
    x = edge[0]
    y = edge[1]
    union(x, y)

print('Roots:', set(i for i in parent[1:]))

 

Now redundant edges (2, 3) and (4, 5) are added in the graph, forming cycles (1, 2, 3) and (3, 4, 5).

We can detect these redundant edges, using the union-find algorithm.

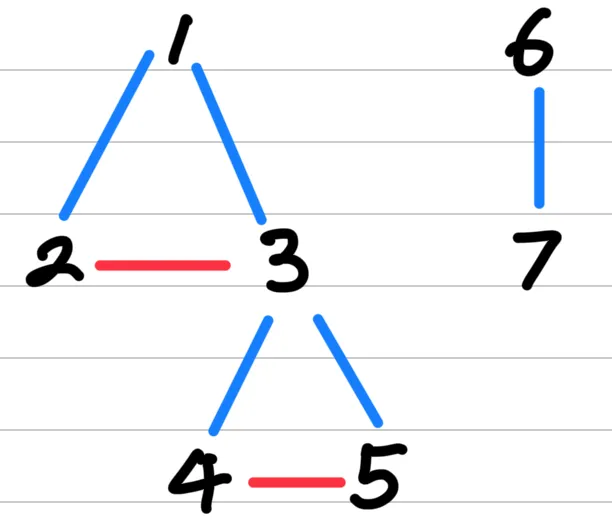
parent = [0, 1, 2, 3, 4, 5, 6, 7]
edges = [(1, 2), (1, 3), (2, 3), (3, 4), (3, 5), (4, 5), (6, 7)]
cycles = []

def find_root(x):
    if parent[x] != x:
        parent[x] = find_root(parent[x])
    return parent[x]

def union(x, y):
    root_x = find_root(x)
    root_y = find_root(y)
    if root_x != root_y:
        parent[root_y] = root_x
    else:
        cycles.append((x, y))

for edge in edges:
    x = edge[0]
    y = edge[1]
    union(x, y)

print('Roots:', set(i for i in parent[1:]))
print('Cycles:', cycles)

 

Key idea: Cycle-forming edges = Edges connecting nodes that have the same root = Redundant edges.