2022.10.05 - [확률론과 수리통계] - 이산확률변수, 확률질량함수, 이산분포, 누적분포함수
확률변수 $X$가 모수가 $(n,p)$인 이항분포(Binomial Distribution; 二项分布)를 따를 때, $X \sim \mathrm{Bin}(n,p)$라고 표현하고, $X$는 다음과 같은 PMF를 갖는다:
$$
f_{X}(x)={n \choose x}p^{x}(1-p)^{n-x}
$$
이항분포의 확률변수 $X$, 모수 $(n,p)$는 다음과 같은 의미를 갖는다:
$\space$
$X$: $n$번의 독립적인 베르누이 시행에서 성공 횟수.
$n$: 베르누이 시행의 횟수.
$p$: 각 베르누이 시행의 성공 확률.
$\space$
여기서 각 베르누이 시행이 독립(Independent; 独立)이라는 조건이 중요하다. 이항분포의 PMF는 $n$개의 확률의 곱으로 표현되는데, 서로 다른 사건의 확률을 곱할 수 있다는 것은 독립을 의미하기 때문이다.
note: 일반적으로 $P(A \cap B)=P(A)P(B \mid A)$인데, 사건 $A$와 $B$가 독립이면 $P(A \cap B)=P(A)P(B)$이다.
예를 들어, 성공확률이 $0.3$인 베르누이 시행을 독립적으로 10번 했다고 하자. 이 10번의 시행 중 성공을 몇 번이나 했는지, 그럴 확률은 얼마인지에 관심이 있을 것이다. 시행의 결과로서 가능한 경우 중 하나인 ‘6번의 성공’을 생각해보자. 이 ‘5번의 성공’이라는 결과도 성패의 순서에 따라서 다음과 같이 여러가지로 나뉠 것이다.
$\space$
결과 1: 실패, 성공, 성공, 성공, 성공, 실패, 성공, 성공, 실패, 실패
결과 2: 성공, 실패, 성공, 실패, 성공, 실패, 성공, 실패, 성공, 성공
결과 3: 실패, 성공, 성공, 성공, 성공, 성공, 실패, 성공 ,실패, 실패
…
$\space$
어느 결과이든 그 결과가 나올 확률은 $(0.3)^{6}(0.7)^{4}$으로 동일하다. 그렇다고 해서 3번 성공할 확률을 $(0.3)^{6}(0.7)^{4}$이라고 할 수는 없다. 위에서 보았듯이 6번 성공한다는 사건은 여러 사건의 합으로 이루어져 있기 때문이다. 대신에 각 결과가 나올 확률을 더해야 하는데, 그 값은 전부 $(0.3)^{6}(0.7)^{4}$으로 동일하므로 이런 결과들이 몇 개가 존재하는가만 알면 된다. 사안의 경우 총 10개의 자리에서 ‘성공’이 들어갈 자리 6개를 선택하는 것이므로 ${10 \choose 6}$개가 있다. 그러므로 6번 성공할 확률 $f_{X}(6)={10 \choose 6}(0.3)^{6}(0.7)^{4}$이다. 이것을 일반화 하면 이항분포의 PMF를 얻는다.
note: 이항분포의 PMF에서, 앞의 ${n \choose x}$는 이항계수(Binomial Coefficient; 二项式系数)라고한다. 이것이 바로 ‘이항’분포의 어원이다.
이항분포의 PMF를 관찰하면, $n=1$일 때 베르누이분포의 PMF와 같다는 것을 알 수 있다. 이항분포는 베르누이 분포의 일반화라고 볼 수 있는 것이다. 베르누이 분포가 1번의 베르누이 시행을 묘사한다면, 이항분포는 $n$번의 독립적인 베르누이 시행을 묘사한다. 기호로는 다음과 같이 나타낼 수 있다:
$$
\mathrm{Bern}(p)=\mathrm{Bin}(1,p)
$$
이제 이것을 수학적으로 나타내기 위해, 독립항등분포(Independent and Identically Distributed, i.i.d.; 独立同分布)라는 개념을 도입하겠다. 여러 확률변수들이 독립항등분포라는 것은 ‘각 확률변수의 분포가 같으면서’(항등) ‘서로 영향을 미치지 않는다(독립)’라는 뜻이다.
확률변수 $X_{i}, , i \in {1,2,\cdots,n}$가 i.i.d.이고 $X_{i} \sim \mathrm{Bern}(p)$라고 하자. 이때 $X:=\sum_{i=1}^{n}X_{i}$라고 정의하면 $X \sim \mathrm{Bin}(n,p)$이다. 쉽게 말해, 이항분포를 따르는 확률변수는 서로 독립적인 베르누이 확률변수의 합으로 이루어져 있다는 것이다. 이항분포의 정의가 $n$번의 독립적인 베르누이 시행에 근거한 것임을 생각하면 당연한 사실이다.
2022.10.06 - [확률론과 수리통계] - 베르누이 분포
note: i.i.d.인 여러 확률변수를 더해서 새로운 분포를 만드는 것은 모델링에 자주 쓰이는 방법 중 하나다. ‘더한다’기 보다는 합성곱(Convolution; 卷积) 연산을 한다고 표현하는 것이 적절하다.
이제 이항분포를 그래프로 나타내보자. 위의 예시인 $X \sim \mathrm{Bin}(10,0.3)$을 그릴 것이다.

그래프에서 보이듯, $P(X=2)$나 $P(X=3)$의 값이 비교적 높다. 즉 10회의 시도 중, 2번이나 3번 성공할 확률이 비교적 크다. 반면에, 단 한번도 성공하지 못할 확률 $P(X=0)$은 각 시행의 성공확률이 0.3으로 작음에도 불구하고 작다. 당연히 10번 모두 성공할 확률 $P(X=10)$은 0에 가까운 값으로, 값이 너무 작아 그래프로도 나타내지 못한다.
그림에서 붉은 부분은 누적분포함수를 표현한 것이다. 붉은 막대의 확률 값을 전부 더하면, $P(X \le 3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)=0.650$이다. 즉, 성공횟수가 3이하일 확률이 0.650이고, 이는 성공횟수가 3을 초과할 확률 0.350보다 크다.
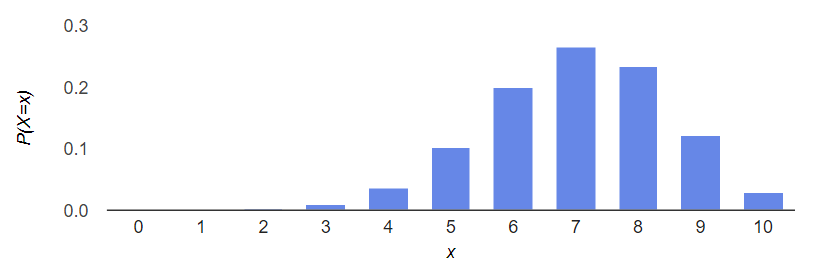
분포는 왼쪽에 몰려있는데, $p=0.3 < 0.5$이기 때문이다. 그렇지만 형상만 놓고 보면 좌우대칭에 가깝긴 한데, 이것은 $p=0.3$이 $0.5$에 가까워서 그렇다. $p=0.5$로 놓으면 그래프는 완벽한 대칭이 된다. $p=0.7$이면 또 어느정도 비대칭이 되는데, 이 그림과는 반대로 오른쪽에 더 많이 분포할 것이다. 예를 들어 $X \sim \mathrm{Bin}(10,0.5)$와 $X \sim \mathrm{Bin}(10,0.7)$의 그래프는 각각 다음과 같다.

만약 정규분포(Normal Distribution; 正态分布)의 그래프를 본적이 있다면, 이 그래프들이 그것과 비슷하다는 점을 눈치챘을 것이다. 왠지 모르게 모수 $n$을 늘리면 그래프가 더 조밀해지고, 정규분포 곡선과 비슷해질 것이라는 예감이 든다. $n=100$, $p=0.3$으로 놓고 그려보자.
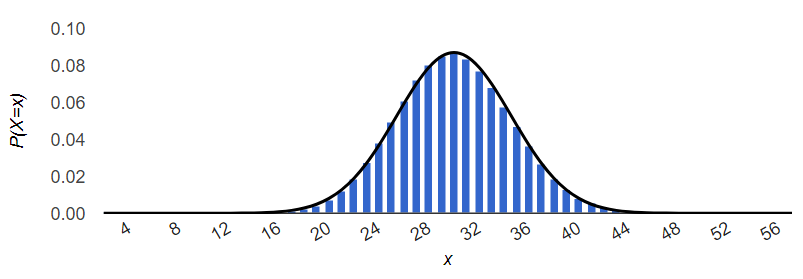
이항분포에서 $n$이 충분히 크다면, 정규분포에 가까워짐을 알 수 있다. 이를 두고, 이항분포의 정규근사(Normal Approximation; 正态近似)라고 한다. 놀라운 사실은, $p=0.3$일 때, $n=10$정도로 작으면 분포가 비대칭적임을 한 눈에 알 수 있는 데 반해, 같은 조건에서 $n=100$정도로 충분히 크면 그래프가 좌우대칭처럼 보인다는 것이다.
note1: 이항분포의 정규근사를 하려면 모수 $(n,p)$가 다음과 같은 조건들을 만족해야 한다: (1) $n \ge 30$; (2) $np \ge 5$; (3) $n(1-p) \ge 5$. 즉 $n$이 충분히 크고, $p$가 0이나 1에 가까운 값이 아닐 때만 이항분포를 정규분포로 근사할 수 있다. $p$가 0이나 1에 가까운 값이라면, 푸아송 분포로 근사하는 것이 바람직하다.
note2: 분포의 비대칭도를 측정하는 통계량은 왜도(Skewness; 偏度)라고 하며, 왜도가 양수 또는 음수일 때 분포는 각각 좌측, 우측으로 집중되고, 0일 때 좌우 고르게 분포한다. 이항분포의 왜도는 $\frac{1-2p}{\sqrt{np(1-p)}}$이고, $n$이 커질 때 왜도 값은 0으로 가까워진다.


