#1. 이산확률변수와 확률질량함수
이산확률변수에 대해, 확률질량함수의 정의는 다음과 같다.
$$
f_{X}(x):=P(X=x)
$$
왜 이런 정의가 필요한 것일까? 다음과 같은 전형적인 예제를 통해 이해해보자.
$\space$
“상자 안에 검은공 60개와 빨간공 40개가 있다. 상자에서 한꺼번에 10개의 공을 꺼냈을 때, 검은공이 2개 나올 확률은 얼마일까?”
$\space$
이 문제의 정답이 ${60 \choose 2}{40 \choose 8}/{100 \choose 10}$라는 것은 쉽게 알 수 있다. 그러면 검은공이 3개일 확률은 얼마일까? 역시 ${60 \choose 3}{40 \choose 7}/{100 \choose 10}$이라고 쉽게 계산할 수 있다. 이런 방식으로 검은공이 0개, 1개, 2개, ..., k개일 확률을 다음과 같이 계산할 수 있다.
$$
\begin{split}
P\left(\lbrace\mathrm{검은공이}\enspace{\color{red}0}\mathrm{개}\rbrace\right)
&={60 \choose {\color{red}0}}{40 \choose {\color{red}{10}}}/{100 \choose 10}
\\
P\left(\lbrace\mathrm{검은공이}\enspace{\color{red}1}\mathrm{개}\rbrace\right)
&={60 \choose {\color{red}1}}{40 \choose {\color{red}9}}/{100 \choose 10}
\\
P\left(\lbrace\mathrm{검은공이}\enspace{\color{red}2}\mathrm{개}\rbrace\right)
&={60 \choose {\color{red}2}}{40 \choose {\color{red}8}}/{100 \choose 10}
\\
\vdots
\\
P\left(\lbrace\mathrm{검은공이}\enspace{\color{red}k}\mathrm{개}\rbrace\right)
&={60 \choose {\color{red}k}}{40 \choose {\color{red}{10-k}}}/{100 \choose 10}
\end{split}
$$
식에서 빨간색 부분을 관찰하면 규칙이 보일 것이다. 그리고 뭔가 규칙이 보이면 일반화를 해줘야 제맛이다. 검은공이 나올 개수를 확률변수 $X$로 놓자. 그러면 $X$는 0, 1, 2, ...의 값을 가질 것이다. 확률변수 $X$가 가질 수 있는 값들을 확률변수 $X$의 관측값(Observation; 观测值)이라고 한다.
확률변수 $X$의 관측값을 $x$로 놓자. 그러면 사건 $\lbrace\mathrm{검은공이}\enspace x\mathrm{개}\rbrace
=\lbrace X=x\rbrace$으로 나타낼 수 있고, 다음이 성립한다.
$$
P\left(\lbrace\mathrm{검은공이}\enspace x\mathrm{개}\rbrace\right)
=P\left(\lbrace X=x \rbrace\right)
$$
이제 사건을 숫자로 나타낼 수 있게 되었다. 표기가 간편해진 것이다. 이것이 바로 확률변수(Random Variable, RV; 随机变量)의 개념이다. 매번 검은공이 어쩌구...이야기하려면 불편하니까 그것을 숫자로 나타낸 것이다.
그리고 어차피 숫자로 쓸거면 집합기호인 $\lbrace \cdot \rbrace$도 귀찮으니 떼버리자. 그러면 다음과 같이 쓸 수 있다.
$$
P\left(\lbrace\mathrm{검은공이}\enspace x\mathrm{개}\rbrace\right)
=P\left( X=x \right)
$$
여기서 $P\left( X=x \right)$는 관찰값 $x$의 값에 따라 결정될 것이다. 그러므로 확률변수 $X$가 $x$라는 값을 가질 확률 $P\left( X=x \right)$는 $x$에 관한 함수이다. 그러므로 다음과 같이 함수 $f_{X}(x)$를 정의하고, 확률질량함수(Probability Mass Function, PMF; 概率质量函数)라고 부르자.
$$
f_{X}(x):=P(X=x)
$$
note: 왜 확률‘질량’함수라는 이름이 붙었는지에 대한 고찰.
2022.10.02 - [확률론과 수리통계] - 확률밀도와 확률질량의 이해
여기서 주의할 점은 관측값 $x$는 아무 숫자나 될 수 없다는 점이다. 확률변수 $X$를 ‘검은공의 개수’로 정의했으므로 그 값은 0,1,2... 같은 음이 아닌 정수이고, 0.5와 같은 값은 가질 수 없다. 이렇게 확률변수 $X$가 뚝뚝 떨어진 값을 가질 때, $X$를 이산확률변수(Discrete RV; 离散型随机变量)라고 한다.
note: 즉, 확률질량함수는 이산확률변수에 대해 정의되는 개념이다. 연속확률변수에 대해서는 확률밀도함수가 별도로 있다.
2022.10.14 - [확률론과 수리통계] - 연속확률변수, 확률밀도함수, 연속분포, 누적분포함수
그런데, $x$가 음이 아닌 정수이더라도 아무 값이나 가질 수 없다. 예제에서 상자 안의 검은공의 개수는 총 60개이다. 그러므로 확률변수 $X$의 관측값 $x$도 0~60까지만 의미가 있다. 예제에서 검은공이 61개가 나올 수는 없는 것이다. 상상속에서는 가능하지만, 실제 응용에서는 의미가 없다.
‘의미가 없다’는 것을 확률이 0이라고 하자. 그러면 $f_{X}(-1)=f_{X}(0.5)=f_{X}(61)=0$이다. 정확히는 $x \in \lbrace 0,1,2, \cdots, 60\rbrace$일 때만 $f_{X}(x)={60 \choose x}{40 \choose 10-x}/{100 \choose 10}$이고, 그게 아닌 다른 값을 가진다면 $f_{X}(x)=0$이다. 즉, 다음과 같이 나타낼 수 있다.
$$
f_{X}(x)=
\begin{cases}
{60 \choose x}{40 \choose 10-x}/{100 \choose 10}, & x \in \lbrace 0,1,2, \cdots, 60\rbrace
\\
0, & \mathrm{otherwise}
\end{cases}
$$
집합 $\lbrace 0,1,2, \cdots, 60\rbrace$와 같이, 함수 $f_{X}(x)$의 값이 0이 아니도록 하는 $x$의 범위를 지지집합(Support; 支撑集)이라고 한다. 이제 지시함수(Indicator Function; 指示函数)라는 것을 도입해서 식을 더 간단히 해보자. 지시함수는 다음과 같이 정의되는 함수이다.
$$
\mathbf{1}_{S}(x):=
\begin{cases}
1, & x \in S
\\
0, & x \notin S
\end{cases}
$$
note: 지지집합의 보다 엄밀한 정의는 다음과 같다: 함수 $f(x)$의 값이 0이 아니도록 하는 $x$의 범위의 폐포(Closure, 闭包). 그러나 여기서는 ‘폐포’의 개념은 딱히 중요하지 않으므로 넘어가자.
그러면 $f_{X}(x)$를 다음과 같이 한 줄로 깔끔하게 고쳐쓸 수 있다.
$$
f_{X}(x)=
\mathbf{1}_{\lbrace 0,1,2, \cdots, 60\rbrace}(x){60 \choose x}{40 \choose 10-x}/{100 \choose 10}
$$
그런데 지지집합이든 지시함수든 ${60 \choose x}{40 \choose 10-x}/{100 \choose 10}$에 비해서는 크게 중요하지 않다. 그리고, 어차피 $f$가 $X$의 확률질량함수인 것을 아는 이상, 매번 $f_{X}$로 표기하는 것도 번거로운 일이다. (지금 이 글을 작성하는 데도 엄청난 번거로움을 느낀다.) 그래서 보통 다음과 같이 간략히 나타내어 쓴다.
$$
f(x)={60 \choose x}{40 \choose 10-x}/{100 \choose 10}
$$
이것이 흔히 쓰는 PMF의 형태이다. 추후 작성될 글, 또는 여러 교과서 등에서 간혹 $f_{X}(x)$를 $f(x)$, $P(X=x)$로 쓰거나, 심지어는 $p(x)$, $p_{X}(x)$등을 혼용해도 당황하지 말자. 다만, $f_{X}(x)$가 함수라는 의미, 확률변수의 이름, 관측값의 이름을 모두 담고 있으므로 가장 공식적인 표기이다.
지시함수는 특히 강조해야할 때를 제외하고 대부분의 글에서 생략되는 편이다. 나도 $f_{X}(x)$를 최대한 원칙으로 하겠지만 지시함수를 매번 적지는 않는다.
#2. 이산분포
함수 $f(x)={60 \choose x}{40 \choose 10-x}/{100 \choose 10}$의 식을 알았으니 그것의 그래프를 그려보자. 가로축에 독립변수인 $x$, 세로축에 종속변수인 $P(X=x)=f(x)$를 놓자. $x$의 값이 뚝뚝 떨어져있으므로 그래프도 여러개의 점 또는 막대의 형태로 그려질 것이다. 여기서는 막대의 형태로 그렸다.
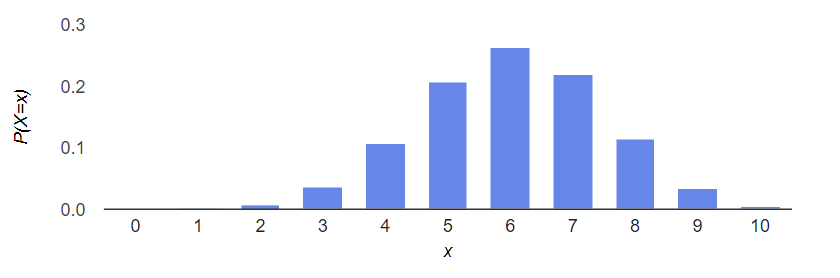
그래프를 보면, $f(6)$의 값이 제일 크다. 즉 $x$의 값이 6일 확률이 제일 크다. 달리 말하면 확률변수 $X$의 관찰값 $x$는 $x=6$ 지점에 많이 분포해있다. 이것이 바로 확률변수의 확률분포(Probability Distribution; 概率分布), 줄여서 분포(Distribution; 分布)의 개념이다. 즉, $x$가 흩어진 모습을 의미하는 것이다. 여기서 확률변수 $X$는 이산확률변수이므로, 이것을 이산분포(Discrete Distribution; 离散分布)라고 부르자.
#3. 이산확률변수의 누적분포함수
잠시 처음의 질문을 떠올려보자.
“상자 안에 검은공 60개와 빨간공 40개가 있다. 상자에서 한꺼번에 10개의 공을 꺼냈을 때, 검은공이 2개 나올 확률은 얼마일까?”
이 질문을 이렇게 바꿔보자.
“상자 안에 검은공 60개와 빨간공 40개가 있다. 상자에서 한꺼번에 10개의 공을 꺼냈을 때, 검은공이 2개 이하 나올 확률은 얼마일까?”
검은공이 2개 이하라는 사건은 검은공이 0개, 1개, 2개가 나올 사건의 합사건이다. 즉, 다음이 성립한다.
$$
\begin{split}
P(X \le 2)
&=P(X=0)+P(X=1)+P(X=2)
\\
&= {60 \choose 0}{40 \choose 10}/{100 \choose 10}+{60 \choose 1}{40 \choose 9}/{100 \choose 10}+{60 \choose 2}{40 \choose 8}/{100 \choose 10}
\end{split}
$$
이런 방식으로, 검은공이 0개 이하, 1개 이하, 2개 이하, ..., k개 이하일 확률도 계산 가능하다.
$$
\begin{split}
P(X \le 0) &=P(X=0)
\\
P(X \le 1) &=P(X=0)+P(X=1)
\\
P(X \le 2) &=P(X=0)+P(X=1)+P(X=2)
\\
\vdots
\\
P(X \le k) &= P(X=0)+P(X=1)+P(X=2)+\cdots+P(X=k)
\end{split}
$$
이렇게 모든 가능한 $k$에 대해 $P(X \le k)$의 값이 존재할 것이다. 이러면 또 이것을 함수의 형태로 일반화하고 싶을 것이다. 그래서 누적분포함수(Cumulative Distribution Function, CDF; 累积分布函数)의 개념을 도입하자. 확률변수 $X$의 CDF는 대문자 $F$를 사용하여 다음과 같이 정의된다.
$$
F_{X}(k):= P(X \le k)
$$
흔히 여기서 $k$를 $x$로 바꾸어, $F_{X}(x):=P(X \le x)$로 쓴다. 중요한 점은 CDF에서 $x$는 관찰값이 아니라는 사실이다. 비교적 혼동을 유발하는 표기법이지만, $X$와 $x$의 한 종류의 문자만 써서 쓸 수 있는 문자를 아껴주기 때문에 헷갈리지 않는 상황에서는 좋은 표기법이다.
note: 이산확률변수를 다룰 때, $f_{X}(x)$와 $F_{X}(x)$의 표기를 원초적인 의미를 나타내는 $P(X=x)$나 $P(X \le x)$로 많이 하는 편인데, 이는 이산확률변수에서 $f(x)=P(X=x)$가 성립하기 때문이다. (정의 그 자체이다.) 그런데 연속확률변수에서는 모든 $x$에 대해 $P(X=x)=0$이므로, 일반적으로 $f(x) \ne P(X=x)$이다. 즉, 함수 $f$, $F$를 이용한 표기는 이산확률변수보다 연속확률변수에서 더 의미가 있다.
PMF와 CDF의 정의를 통해, 임의의 이산확률변수 $X$에 대해 다음이 성립함을 알 수 있다. 이 관계식은 나중에 연속확률변수에서 PDF와 CDF를 정의하는 데 좋은 아이디어를 제공한다.
$$
F_{X}(k)=\sum_{x= -\infty}^{k}f_{X}(x)
$$
결국, 이산확률변수에 대해, 그것의 PMF이든 그래프이든 CDF이든 모두 분포를 표현하는 방식이라고 할 수 있다. 그러므로 PMF, 그래프, CDF를 일컬어 분포라고 한다. 즉 어떤 확률변수의 ‘분포’를 설명하라고 할 때, 그것의 PMF, 그래프, CDF 등을 제시할 수 있는 것이다. 보통은 비교적 원초적인 PMF를 많이 제시하는 편이고, 그것을 시각화할 때 그래프도 함께 제시한다. CDF는 그렇게 중요하게 다뤄지지는 않는다. PMF 값의 합으로 나타내면 되기 때문이다.
분포는 여러가지가 있다. 이번 글에서의 예제에 설정된 상황 외에도, 다른 상황이되면 PMF는 다른 형태의 식, 즉 다른 분포가 될 것이다. 또, 확률변수를 어떻게 정의하는가에 따라서도 수많은 분포들이 나올 것이다. 앞으로 여러가지 이산분포에 대해 정리해보자.
note: 이번 글에서 예제의 분포는 ‘초기하분포’라고 불리는 분포 중 하나일 뿐이다.
2022.10.06 - [확률론과 수리통계] - 베르누이 분포
2022.10.06 - [확률론과 수리통계] - 이항분포
2022.10.06 - [확률론과 수리통계] - 기하분포
2022.10.08 - [확률론과 수리통계] - 음이항분포
2022.10.12 - [확률론과 수리통계] - 푸아송 분포
2022.10.12 - [확률론과 수리통계] - 초기하분포
2022.10.13 - [확률론과 수리통계] - 이산분포 총정리


