확률변수의 수학적인 중심인 기댓값과 관찰값이 흩어진 정도를 나타내는 분산은 각각 1차 원적률과 2차 중심적률로, 분포를 이해하는 데 매우 중요한 정보이지만, 이것만으로는 부족한 감이 있다. 따라서 분포의 비대칭도를 나타내는 왜도와 꼬리의 두께를 나타내는 첨도를 함께 고려하는 경우가 많다. 상관계수처럼 단위의 문제를 없애기 위해, 표준화적률로 정의한다.
기댓값과 분산에 더해 왜도와 첨도를 고려하면, 자연스럽게 적률이 아니지만 분포를 묘사하는 데 중요한 역할을 하는 중앙값, 최빈값, 극단값을 고려하게 된다. 따라서 더욱 정확하게 분포를 묘사할 수 있다.
#1. 왜도
분포의 비대칭도는 왜도(Skewness; 偏度)로 나타낸다. 왜도는 3차 표준화적률이다.
$$ \mathrm{Skew}(X):={\mu}^{\ast}_3=\frac{\bar\mu_3}{\sigma^3}=\frac{\mathbb{E}[(X-\mu)^3]}{(\mathbb{E}[(X-\mu)^2])^{3/2}}=\mathbb{E}\left[\left(\frac{X-\mu}{\sigma}\right)^3\right] $$
왜도는 기댓값(평균), 중앙값, 최빈값의 3가지 중심경향치를 동시에 고려할 때 유용하다. 기댓값은 ‘수학적인 중심경향치’일 뿐이고, 분포의 실제 모습과는 거리가 있다. 실제로 기댓값이 $\mu$라고 해서 데이터가 $\mu$를 중심으로 좌우대칭인 것은 아니다. 이는 $\int_{-\infty}^{\infty}xf(x)\space dx=\mu$가 $f(\mu+x)=f(\mu-x)$를 의미하지 않는 것과 마찬가지이다.
아래 그림처럼, 왜도가 0일 때 분포는 기댓값을 중심으로 좌우대칭일 것이며, 평균=중앙값=최빈값이다. 왜도가 양수이면, 분포는 오른쪽으로 꼬리가 길며, 이때는 최빈값<중앙값<평균의 관계가 성립한다. 왜도가 음수이면, 분포는 왼쪽으로 꼬리가 길며 평균<중앙값<최빈값의 관계가 성립한다.
이처럼 비대칭도는 절대적인 크기 뿐만 아니라 방향도 함께 고려해야 한다. 제곱이 아닌 3제곱을 써서 부호를 살리는 이유다. 그리고 단위의 문제점을 없애기 위해, 먼저 데이터를 표준화한다. 따라서 분포의 비대칭도를 3차 표준화적률로 측정하기로 한다.
왜도를 다룰 때 헷갈리는 점이 바로 왜도의 방향인데, 아래의 두번째 그림은 확률질량이 왼쪽으로 쏠려있으므로 음의 왜도라고 착각하기 쉽다. 하지만 다음과 같은 문장을 기억하면 착각할일이 적다.
$$ 왜도는\enspace꼬리를\enspace기준으로\enspace정한다. $$
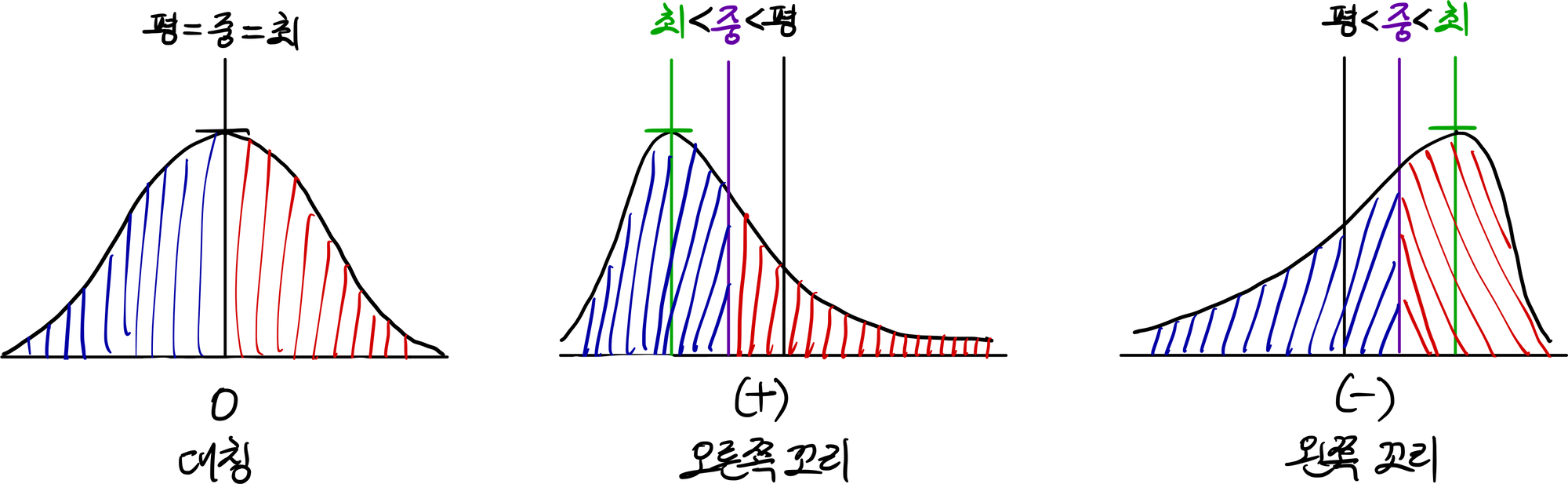
따라서 양의 왜도는 오른쪽으로 꼬리가 있는 형태이고, 음의 왜도는 왼쪽으로 꼬리가 있는 형태이다. 확률질량이 쏠린쪽과 반대방향이다.
#2. 첨도
분포의 비대칭도 외에도, 꼬리 두께에 대해서도 관심을 가져보자. 꼬리가 두꺼울수록 극단값(Outlier; 离群值)이 많다고 여겨진다. 또 꼬리가 얇을수록 극단값이 적고, 확률질량은 중심경향치 주위에 집중된다.
서로 독립인 확률변수 수열이 중심극한정리를 만족하려면 린데베르그 조건을 만족해야 하고, 린데베르그 조건은 꼬리의 분산을 논의하고 있다. 따라서 꼬리 두께는 데이터 과학자들에게 중요한 정보이다.
꼬리의 두께는 첨도(Kurtosis; 峰度)로 측정한다. 첨도는 확률변수의 4차 표준화적률이다.
$$ \mathrm{Kurt}(X):={\mu}^{\ast}_4=\frac{\bar\mu_4}{\sigma^4}=\frac{\mathbb{E}[(X-\mu)^4]}{(\mathbb{E}[(X-\mu)^2])^{4/2}}=\mathbb{E}\left[\left(\frac{X-\mu}{\sigma}\right)^4\right] $$
꼬리의 두께를 나타내는 데는 분산처럼 절대적인 크기가 필요하고, 부호는 중요하지 않다. 그리고 단위의 문제를 없애기 위해 먼저 표준화했다.
첨도를 구하기 위해 4제곱씩이나 하는 이유는 뭘까? 표준화한 확률변수는 분포 중심과 가까이 있을 수록, 4제곱한 값이 비교적 작다. 반면 분포에서 멀리 떨어진, 극단값들은 4제곱하면 비교적 크다. (일반적으로 $\mu\pm3\sigma=\pm3$ 범위 밖을 극단값으로 잡으며, 이것을 4제곱한 값은 굉장히 크다.)
따라서 첨도의 크기에 영향을 주는 것은 꼬리쪽의 극단값이고, 중심에 가까운 쪽은 첨도의 크기에 주는 영향이 미미하다.
note1: 이런 측면에서 볼 때 ‘첨도’라는 이름은 적절하지 않다. 첨도의 정의는 분포의 꼬리 두께, 극단값의 많고 적음을 나타내기 위함임을 생각하자. 그런데 ‘첨도’는 뾰족함을 강조하고 있다. 후술할 중첨, 저첨, 고첨에 대응하는 영어 수식어인 Meso(중간), Platy(가로로 평평한), Lepto(세로로 뾰족한) 모두 ‘뾰족함’을 강조한다. 이는 중국어 中、低、尖도 마찬가지다.
note2: 최근 문헌을 보면, Platykurtic(가로로 평평한 봉우리) 대신 Thin Tail(얇은 꼬리), Leptokurtic(세로로 뾰족한 봉우리) 대신 Fat Tail(뚱뚱한 꼬리)이라는 용어를 쓰기도 한다. 中尾(중간 꼬리)、瘦尾(날씬한 꼬리)、肥尾(뚱뚱한 꼬리)처럼 중국어 문헌도 꼬리의 두께를 강조하는 것이 많이 보인다.
그런데, 첨도의 ‘기준’은 뭘까? 첨도가 꼬리의 두께를 측정한다면, 분명 ‘얇은’ 꼬리와 ‘두꺼운’ 꼬리를 생각하게 될 것이다. 그렇다면 얇지도 않고 두껍지도 않은 ‘적당한 두께’의 꼬리를 나타내는 첨도는 무엇일까?
중심극한정리의 목표는 확률변수의 합을 정규분포에 분포수렴하도록 만드는 것이다. 정규분포는 통계학의 심장과도 같은 매우 중요한 분포이므로, 이를 ‘기준’으로 삼기로 하자.
정규분포의 첨도를 구해보면 3이다. 이 상태를 중첨(Mesokurtic; 中峰)이라고 하자. 3보다 작은 첨도는 저첨(Platykurtic; 低峰), 3보다 큰 첨도는 고첨(Leptokurtic; 尖峰)이라고 한다.
그런데 일반적으로 ‘3’을 기준으로 하는 것 보다는 ‘0’을 기준으로 하는 것이 익숙하다. 따라서 다음과 같이 초과첨도(Excess Kurtosis; 超额峰度)를 원래 첨도에서 3을 뺀 것으로 정의하고, 초과첨도를 기준으로 꼬리 두께를 논의하는 것이 일반적이다.
$$ \mathrm{ExKurt}(X):=\mathrm{Kurt}(X)-3 $$
초과첨도의 정의에 의해, 중첨은 초과첨도가 0이고, 저첨과 고첨은 각각 초과첨도가 음수와 양수이다. 꼬리의 관점으로 표현하면, 초과첨도가 (-)일 때 꼬리가 얇고 극단값이 정규분포의 예측에 비해 적다. 초과첨도가 (+)일 때 꼬리가 두껍고 극단값이 정규분포의 예측에 비해 많다. 첨도는 항상 정규분포를 기준으로 논의되어야 한다.
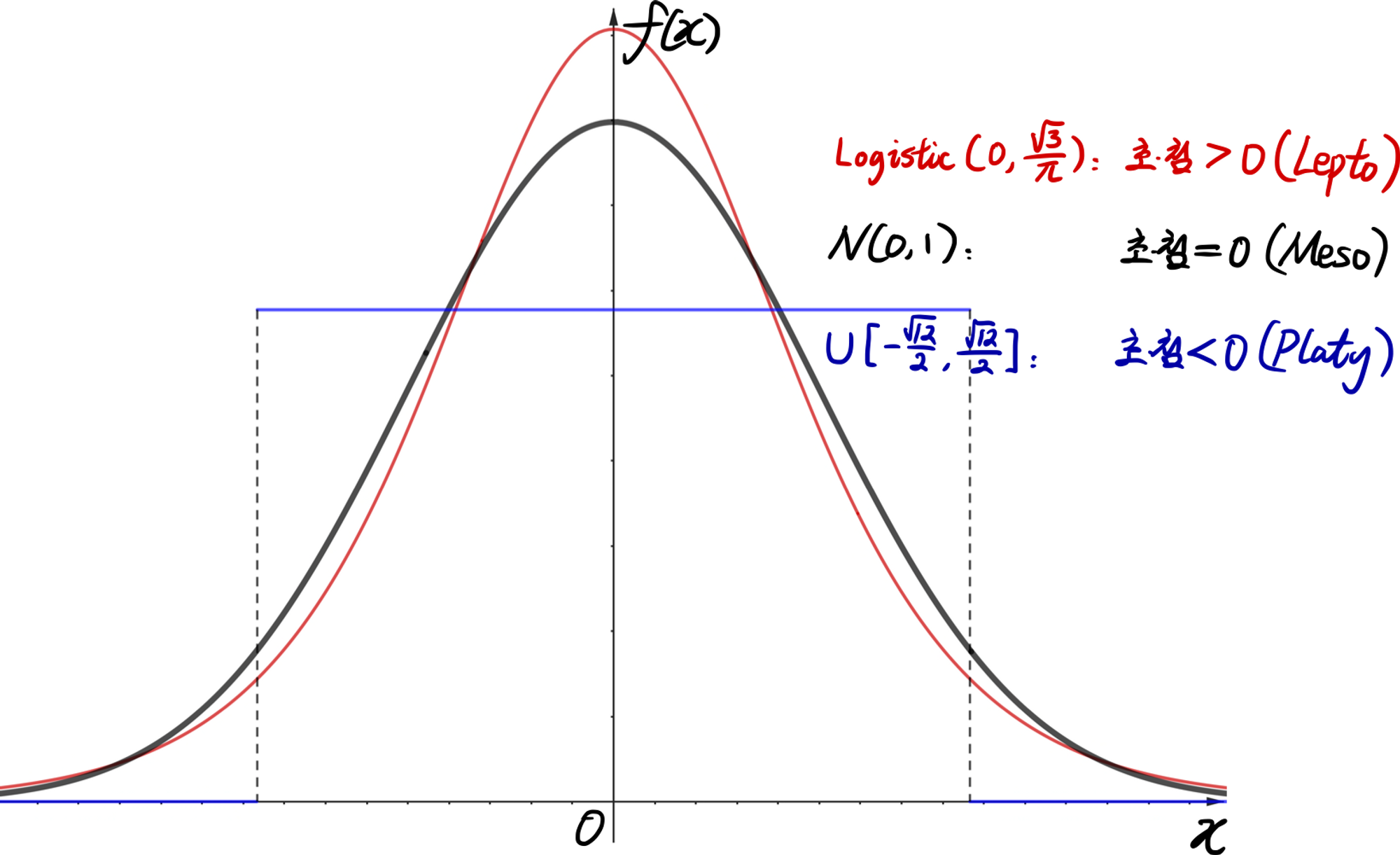

한편, 첨도를 가지고 꼬리 두께를 논의할 때 중요한 사항이 있다. 바로 분포의 대칭축과 분산을 통일해야 한다는 것이다. 같은 첨도일지라도 분산, 즉 데이터가 흩어진 정도에 따라 꼬리 두께는 바뀐다. 그리고 대칭축이 다르면 제대로 된 비교를 하기 어렵다. 따라서 평균과 왜도를 0으로 고정하고, 분산은 1로 고정한다. 이는 표준정규분포의 적률과 같다.

가장 대표적인 것이 정규분포로, 정규분포는 모수가 무엇인가에 상관없이 첨도가 모두 상수 3으로 고정이다. (초과첨도는 0으로 고정.) 하지만 분산을 달리하면, 꼬리의 ‘두께’는 바뀐다.
note: 첨도가 모수와 관계없는 상수라는 것은 어떤 의미일까? 정규분포는 모수를 달리해도 ‘정규분포의 모습을 간직하고 있다’. 그 외 수많은 분포들이 모수를 달리해도 생김새는 비슷한데, 평균이나 분산정도는 바뀔 수도 있지만, 왜도나 첨도같은 고차적률은 결국 상수가 되어버리기 때문이 아닐까? 모수에 따라 분포의 모습이 천차만별인 베타분포 같은 경우, 왜도와 첨도가 모수에 따라 영향을 받는다는 사실은 이 추측에 부합한다.
이런 점에서 첨도는 조심스럽게 논의되어야 하는 개념이다. 어쩌면 분포의 꼬리를 묘사하는 더 좋은 방법이 있을지도 모른다.
그럼에도 불구하고 첨도는 왜도와 함께 정규성검정(Normality Test; 正态性检验)에서 이용되는 개념이기 때문에 중요하다. 쉽게 말해 어떤 데이터가 정규분포를 따르는지 아닌지를 판단할 때 초과첨도와 왜도가 0에 가까운지 살펴보는 것이다.
'Mathematics' 카테고리의 다른 글
| 누율생성함수, 누율 (2) | 2023.01.30 |
|---|---|
| 물리량과 적률의 비교 (0) | 2023.01.29 |
| 적률, 적률생성함수 (0) | 2023.01.25 |
| 라플라스 근사 (2) | 2023.01.23 |
| 스털링 근사 (2) | 2023.01.23 |



