누율생성함수와 누율은 수리통계학에서 비교적 마이너한 주제이지만, 그래도 어떤 문제에 부딪혔을때 그것을 우회적으로 해결하는 방법론을 제시하기 때문에 정리해둔다. 로그를 씌워 계산을 편리하게 만드는 것, 그리고 복잡한 다항식을 다루는 것 모두 큰 공부가 되었다.
note: 제목이 ‘누율, 누율생성함수’가 아닌 이유=누율생성함수를 먼저 정의하고 그 다음 누율을 정의한다는 사실을 기억하기 위함.
#1. MGF의 또 다른 문제점
지난 글에서 소개한 적률과 적률생성함수는 존재성 외에도 또 하나 문제점이 있는데, 바로 ‘미분친화적이지 않다’는 것이다.
예를 들어 모든 정규분포의 왜도와 첨도가 항상 0과 3임을 보이기 위해서 먼저 다음과 같이 적률생성함수를 계산하고,

그리고 이렇게 구한 적률생성함수를 3, 4번 미분하고, 거기에 $t=0$, $\mu=0$, $\sigma^2=1$을 대입해야 비로소 3, 4차 표준화 적률인 왜도와 첨도가 구해진다.

계산이 정말 복잡했다. MGF가 ‘미분친화적이지 않다’는 것은 바로 이것을 의미한다. 4차까지만 했으니까 그나마 나은데, 고차원으로 갈 수록 더 복잡해질 것이다.
정규분포의 MGF만 그런가 싶어서 찾아봤더니 다른 분포는 더 복잡하다. 이러면 MGF를 도무지 써먹을 수가 없다. 이론적으로는 적률을 무한히 생성할 수 있어도 실제로 계산에 착수해보면 너무나도 복잡해서 응용가치가 떨어진다.
#2. 누율생성함수
#2.1 로그를 씌워보자
정규분포의 MGF가 미분친화적이지 않은 이유는 바로 다항식이 지수자리에 위치하고 있어서 그렇다. $e^{f(t)}$를 미분하면, 1계에서 $e^{f(t)}f^{\prime}(t)$, 2계에서 $e^{f(t)}[f^{\prime}(t)^2+f^{\prime\prime}(t)]$, 3계에서 $e^{f(t)}[f^{\prime}(t)^3+3f^{\prime}(t)f^{\prime\prime}(t)+f^{\prime\prime\prime}(t)]$처럼 미분을 할 수록 복잡해진다.
만약 정규분포의 MGF가 $e^{f(t)}$의 형태가 아니라 $f(t)$의 형태라면 미분이 편할 것이다. 따라서 자연스럽게 로그를 씌워보자는 생각을 하게 된다.
$$
f(t)=\ln e^{f(t)}
$$
바로 이것이 누율생성함수(Cumulant Generating Function, CGF; 累积量母函数)의 핵심 아이디어다. 누율생성함수는 다음과 같이 MGF에 로그를 씌운 형태로 정의된다.
$$
K_X(t):=\ln M_X(t)
$$
#2.2 매클로린 급수 형태로 고치자
다음과 같이 MGF에 로그를 씌워 CGF를 만들었다. 함수에 일종의 변환을 한 셈인데, 원래 하던 방법처럼 적률을 얻을 수 있을까?
$$
K_X(t)=\ln\left(1+\mu_1t+\mu_2\frac{t^2}{2!}+\mu_3\frac{t^3}{3!}+\cdots\right)
$$
적률생성함수처럼 $n$번 미분해서 $n$차 원적률을 얻으려면, 누율생성함수도 매클로린 급수 형태여야 한다. 따라서 누율생성함수를 매클로린 전개할 것이다. $\ln(1+x)$의 매클로린 전개가 잘 알려져있으므로 이것을 이용하자.
$$
K_X(t)=\ln(1+S)=S-\frac{S^2}{2}+\frac{S^3}{3}-\frac{S^4}{4}+\cdots
\\[2ex]
S:=\sum_{n=1}^{\infty}\mu_n\frac{t^n}{n!}
$$
이 식은 반드시 $t^n(n=1,2,\cdots)$에 관한 다항식으로 정리될 것이다. 목표는 MGF와 비슷하게 만드는 것이므로 우선 다음과 같이 정리된다고 가정하자. (만약 아니라면 나중에 수정하면 그만이다.)
$$
\begin{split}
&M_X(t)=1+\sum_{n=1}^{\infty}\mu_n\frac{t^n}{n!}
\\[4ex]
&\therefore K_X(t)\overset{?}{=}\sum_{n=1}^{\infty}\kappa_n\frac{t^n}{n!}\cdots(1)
\end{split}
$$
#3. 누율
#3-1. 정의와 의미
식 (1)에서 $\kappa_n$을 확률변수 $X$의 $n$차 누율(Cumulant; 累积量)이라고 한다. 누율생성함수는 MGF와 작동원리가 완벽히 같다. $n$차 누율을 생성하고 싶다면 누율생성함수를 $n$번 미분하고, $t=0$을 대입하면 된다.
$$
K_X^{(n)}(0)=\kappa_n
$$
그럼 이 누율은 무슨 의미가 있을까? CGF를 $t^n/n!$에 관한 다항식으로 정리할 때 앞에 붙는 계수가 바로 누율이다. 이 계수들은 $\mu_n$에 관한 다항식이다. 즉, 누율은 적률을 이용해서 계산될 수 있다.
$$
\kappa_n=\mu_n에\enspace관한\enspace다항식
$$
이를 뒤집어서, 적률을 누율을 이용하여 계산할 수도 있을 것이다.
$$
\mu_n=\kappa_n에\enspace관한\enspace다항식
$$
#3-2. 계산
이제 적률은 누율을 이용해서 계산할 수 있음을 알았고, 남은 것은 누율을 계산하는 것이다. 누율은 $K_X(t)$을 정리했을 때 $t^n/n!$의 계수이다. 이 계수를 구해야한다. 지금까지의 상황을 정리하면 다음과 같다.
$$
\begin{split}
K_X(t)&=S-\frac{S^2}{2}+\frac{S^3}{3}-\frac{S^4}{4}+\cdots,\space
S:=\sum_{n=1}^{\infty}\mu_n\frac{t^n}{n!}
\\
&\overset{?}{=}\sum_{n=1}^{\infty}\kappa_n\frac{t^n}{n!},\space\kappa_n=?
\end{split}
$$
우선 쉬운 것 부터 생각해보자. $t=t^1/1!$의 계수는 뭘까? $K_X(t)$의 첫번째 항인 $S$에서만 $t$라는 것이 만들어진다. 따라서 $t$의 계수는 $\mu_1$이고, 이는 $\kappa_1=\mu_1$을 의미한다.
다음으로 $t^2/2!$의 계수를 뽑아내보자. 우선 $S$에서 $\mu_2(t^2/2!)$을 찾을 수 있다. 그리고 $-S^2/2$에서 $(\mu_1t)^2\cdot(-1/2)$을 찾아낼 수 있다. 그 뒤로는 찾을 수 없다. 이것을 전부 더하면
$$
\mu_2\frac{t^2}{2!}+(\mu_1 t)^2\left(-\frac{1}{2}\right)=(\mu_2-\mu_1^2)\frac{t^2}{2!}
$$
이므로, $\kappa_2=\mu_2-\mu_1^2$이다. 지금까지 1, 2차 누율을 계산했는데 각각 평균과 분산이다. 혹시 3차 누율은 왜도일까? 기대를 가지고 계산을 해보자.

3차 누율은 왜도가 아니라 3차 중심적률이다. 그래도 왜도와 비슷하므로 좋은 결과이다.
지금까지의 계산결과로는 아직 4차 적률이 등장하지 않았다. 4차 적률은 4차 누율을 계산할 때 반드시 등장할 것이다. 4차 누율을 구해보면

4차 누율은 조금 깊게 생각해야 하는 편이었다. $t^4$를 만드는 경우의 수가 제법 많기 때문이다. 그래도 규칙성을 가지고 차근차근 분석해보면, 결국 4라는 자연수를 $\mathbb{N}^{+}$으로 합분해하는 문제로 치환할 수 있다.
4차 누율을 보고 뭔가 떠오르는 것은 없다. 그런데 식이 뭔가 4제곱을 전개한 것 같으므로 최대한 4차 중심적률과 연관지어보자.
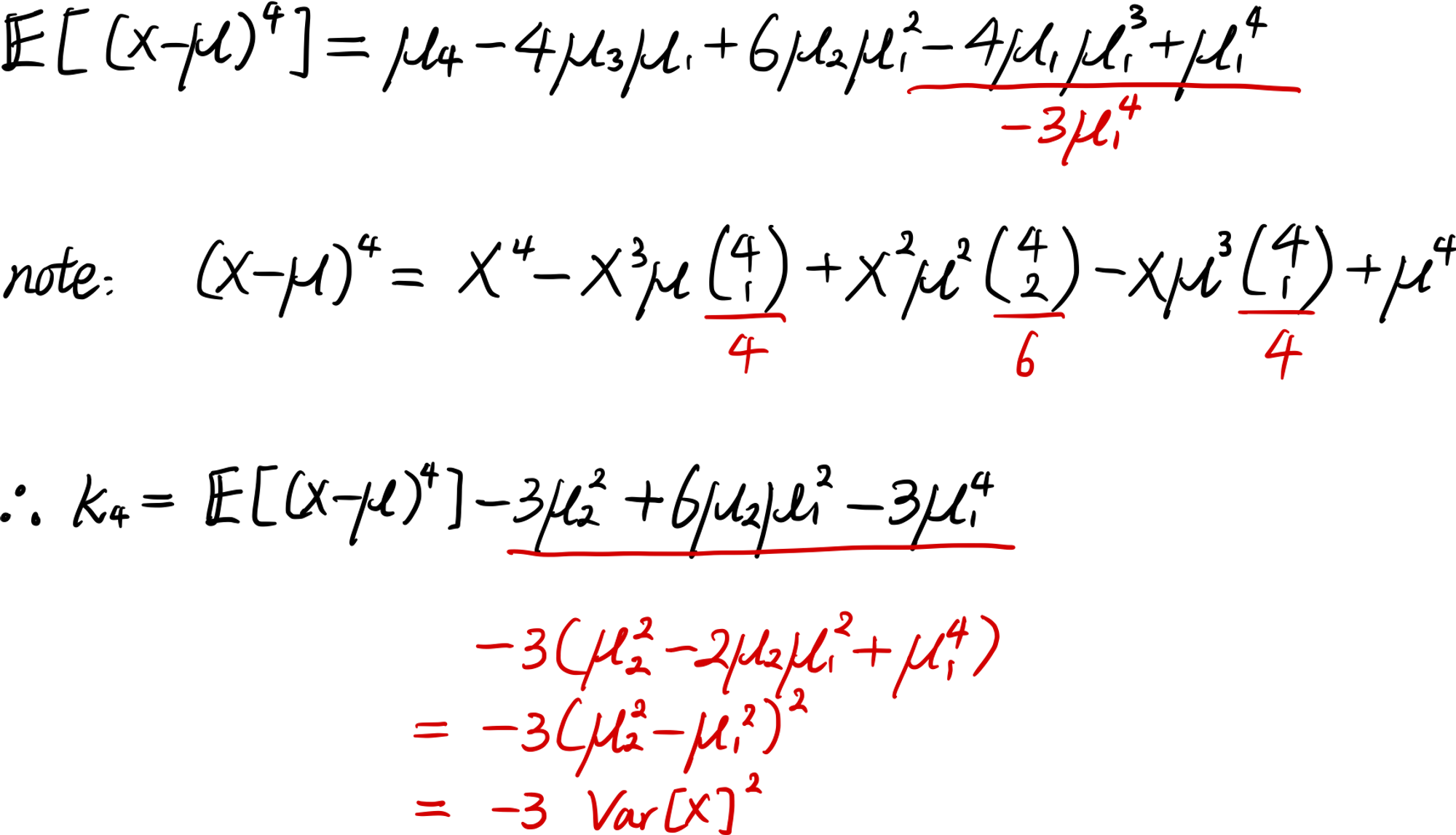
#4. 정리, 요약, 생각
#4-1. 적률과 누율의 관계식
지금까지 구한 1, 2, 3, 4차 누율을 정리하면 다음과 같다.
$$
\begin{split}
&\kappa_1=\mu_1
\\
&\kappa_2=\mu_2-\mu_1^2
\\
&\kappa_3=\mu_3-3\mu_2\mu_1+2\mu_1^3
\\
&\kappa_4=\mu_4-4\mu_3\mu_1-3\mu_2^2+12\mu_2\mu_1^2-6\mu_1^4
\end{split}
$$
이것을 친숙한 결과로 나타내면
$$
\begin{split}
&\kappa_1=\mathbb{E}[X]
\\
&\kappa_2=\mathrm{Var}[X]
\\
&\kappa_3=\mathbb{E}[(X-\mu)^3]
\\
&\kappa_4=\mathbb{E}[(X-\mu)^4]-3\mathrm{Var}[X]^2
\end{split}
$$
이번에는 반대로 적률을 누율로 나타내보자.
$$
\begin{split}
&\mu_1=\kappa_1
\\
&\mu_2=\kappa_2+\kappa_1^2
\\
&\mu_3=\kappa_3+3\kappa_2\kappa_1+\kappa_1^3
\\
&\mu_4=\kappa_4+4\kappa_3\kappa_1+3\kappa_2^2+6\kappa_2\kappa_1^2+\kappa_1^4
\end{split}
$$
계수가 통계역학의 Cluster Expansion(集团展开)과 닮았다. 우연일까?
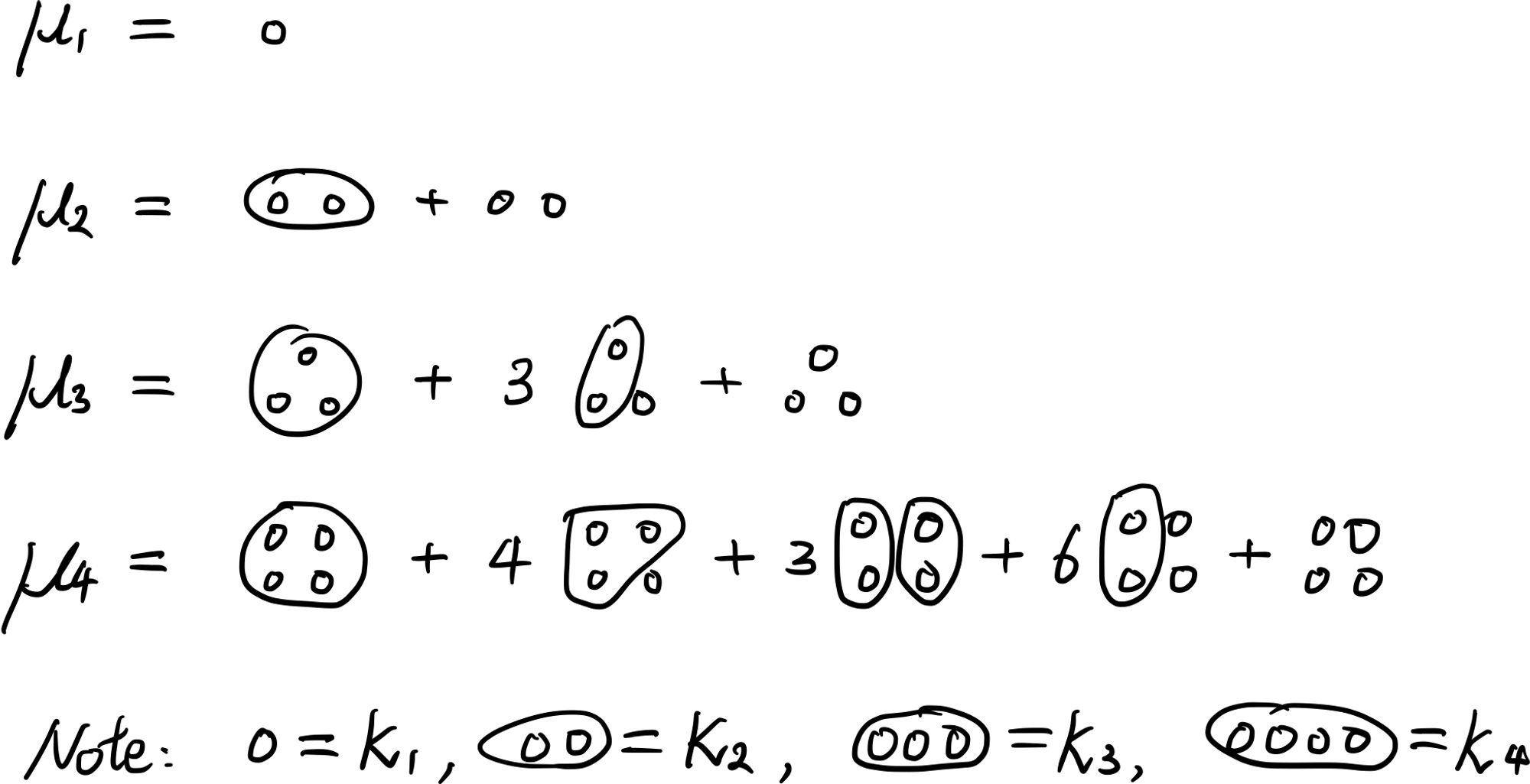
#4-2. 누율의 성질
누율은 다음과 같은 성질이 있다. $n=1$일 때 기댓값, $n=2$일 때 분산의 성질이다.
(1) $\kappa_n[X+Y]=\kappa_n[X]+\kappa_n[Y](X\perp Y)$
(2) $\kappa_n[aX]=a^n\kappa_n[X]$
이 성질들은 간단하게 보일 수 있다. 먼저 (1)은 누율생성함수가 적률생성함수에 로그를 씌운 것으로 인해 필연적으로 성립한다.
$$
\begin{split}
&M_{X+Y}=M_XM_Y
\\
&\Rightarrow K_{X+Y}=K_X+K_Y
\\
&\Rightarrow K^{(n)}_
{X+Y}(t)=K^{(n)}_
X(t)+K^{(n)}_
Y(t)
\end{split}
$$
note: 여기서도 곱의 미분을 피하려고, 일부러 합으로 찢어놓으려고 로그를 도입했음을 느낄 수 있다. $M^{(n)}_{X+Y}(t)$는 $K^{(n)}_{X+Y}(t)$와 달리 그리 간단하지 않을 것이다. 확률변수가 독립일 때 누율은 가법성을 만족하므로, ‘Cumulant’, 문자 그대로 누적이 가능하다. 그래서 이런 이름이 붙었나?
그리고 (2)를 유도하자. 무의식적 통계학자의 법칙(LOTUS)에 의해 먼저 다음이 성립하고, ($M_{aX}$는 최댓값과 헷갈리니까 여기서는 잠시 b로 놓자.)
$$
M_{bX}(t)=\int_{-\infty}^{\infty}e^{tbX}\space dF_X(x)
$$
누율을 구할 때 정의했던 $S$는 다음과 같이 바뀐다.
$$
S:=\sum_{n=1}^{\infty}b^n\mu_n\frac{t^n}{n!}
$$
$t^n/n!$의 계수를 뽑아내는 과정에서, 자연스럽게 각 항에 $b^n$이 추가될 것이고 이것을 따로 빼면 (2)가 성립한다.
'확률론과 수리통계' 카테고리의 다른 글
| 통계학 기본 용어 정리 (0) | 2023.02.02 |
|---|---|
| 이항정리 (0) | 2023.02.02 |
| 물리량과 적률의 비교 (0) | 2023.01.29 |
| 왜도, 첨도 (0) | 2023.01.26 |
| 적률, 적률생성함수 (0) | 2023.01.25 |



