#1. 정의
확률벡터 $(X,Y)$가 이변량 정규분포(Bivariate Normal Distribution; 二元正态分布)를 따른다는 것을 다음과 같이 나타낸다.
$$ (X,Y)\sim\mathrm{N}(\mu_1,\mu_2,\sigma^2_1,\sigma_2^2,\rho) $$
$(\mu_1,\mu_2,\sigma^2_1,\sigma_2^2,\rho)$는 이변량 정규분포의 모수이며, 다음과 같은 의미를 갖는다.
$\space$
$\mu_1$, $\mu_2$: 각각 $X$와 $Y$의 기댓값이다.
$\sigma_1$, $\sigma_2$: 각각 $X$와 $Y$의 분산이다.
$\rho$: $X$와 $Y$의 상관계수이다.
$\space$
이변량 정규분포의 확률밀도함수는 다음과 같이 주어진다.
$$ f(x,y)=\frac{\exp\left[-\frac{\left(\frac{x-\mu_1}{\sigma_1}\right)^2-2\rho\left(\frac{x-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right)+\left(\frac{y-\mu_2}{\sigma_2}\right)^2}{2(1-\rho^2)}\right]}{2\pi\sigma_{1}\sigma_{2}\sqrt{1-\rho^2}} $$
이변량 정규분포의 확률밀도는 복잡해보이지만, 나름 규칙성을 찾을 수 있다. 특히 일변량 정규분포의 확률밀도와 비교했을 때 감을 잡기 쉽다. 이번 글에서는 일변량 정규분포의 확률밀도를 다음과 같이 나타내자.
$$ \mathrm{N}(x;\mu,\sigma):=\frac{\exp\left[-\frac{(x-\mu)^2}{2\sigma^2}\right]}{\sqrt{2\pi}\sigma}=\frac{\exp\left[-\frac{\left(\frac{x-\mu}{\sigma}\right)^2}{2}\right]}{\sqrt{2\pi}\sigma} $$
#2. 변형
#2.1 두 정규분포의 곱
이변량 정규분포를 식의 변형을 통해 두 정규분포의 곱으로 분리할 수 있다. ($\exp()$의 성질과 완전제곱식을 만드는 방법을 응용함.)
$$ \begin{split} f(x,y)&=\frac{\exp\left[-\frac{\left(x-\mu_1-\rho\frac{\sigma_1}{\sigma_2}(y-\mu_2)\right)^2}{2\sigma_1^2(1-\rho^2)}\right]}{\sqrt{2\pi}\sigma_1\sqrt{1-\rho^2}}\cdot\frac{\exp\left[-\frac{(y-\mu_2)^2}{2\sigma_2^2}\right]}{\sqrt{2\pi}\sigma_2} \\ &=\mathrm{N}\left(x;\mu_1+\rho\frac{\sigma_1}{\sigma_2}(y-\mu_2),\sigma_1^2(1-\rho^2)\right)\cdot\mathrm{N}(y;\mu_2,\sigma_2^2) \end{split} $$
#2.2 이차형식 포함
이변량 정규분포의 PDF는 이차형식을 포함한 형태로 정리될 수 있다. (이차형식 참조.)
$$ f(\mathbf{x;\boldsymbol{\mu},\Sigma})=\frac{ \exp\left[-\frac{1}{2}\mathbf{(x-\boldsymbol\mu)^T}\mathbf\Sigma^{-1}\mathbf{(x-\boldsymbol\mu)}\right] } {2\pi\sqrt{\vert\mathbf{\Sigma}\vert} } $$
이 경우 $\mathbf{X}\sim\mathrm{N}(\boldsymbol{\mu},\mathbf{\Sigma})$와 같이 나타낸다. $\boldsymbol{\mu}$는 기댓값 벡터이고 $\mathbf{\Sigma}$는 공분산 행렬이다.
유도 과정: 먼저 $\exp()$안을 살펴보자.
$$ -\frac{\left(\frac{x-\mu_1}{\sigma_1}\right)^2-2\rho\left(\frac{x-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right)+\left(\frac{y-\mu_2}{\sigma_2}\right)^2}{2(1-\rho^2)} $$
$\frac{x-\mu_1}{\sigma_1}$은 $X$의 관측값을 표준화한 것이고, $\frac{y-\mu_2}{\sigma_2}$ 역시 마찬가지로 $Y$를 표준화한 것이다. 이 둘을 각각 $z_1$, $z_2$로 놓으면, 이 식은 이차형식(Quadratic Form; 二次型)이 된다.
$$ \begin{split} -\frac{z_1^2-2\rho z_1z_2+z_2^2}{2(1-\rho^2)}&=-\frac{1}{2(1-\rho^2)}(z_1,z_2)\begin{pmatrix}1&-\rho\\-\rho&1\end{pmatrix}\begin{pmatrix}z_1\\z_2\end{pmatrix} \\[3ex] &=-\frac{1}{2}\mathbf{z^T}\mathbf{A}\mathbf{z},\space\mathbf{A}=\frac{1}{1-\rho^2}\begin{pmatrix}1&-\rho\\-\rho&1\end{pmatrix},\space\mathbf{z}=\begin{pmatrix}z_1\\z_2\end{pmatrix} \end{split} $$
이것을 다시 원래 확률밀도에 대입하면 식이 확실히 깔끔해지고 눈이 편해진다. 하지만 $\exp()$ 바깥의 상수는 어떻게 처리할 수가 없었고, 영 만족스럽지 못한 결과이다.
$$ f(x,y)=\frac{\exp\left[-\frac{1}{2}\mathbf{z^T}\mathbf{A}\mathbf{z}\right]}{2\pi\sigma_{1}\sigma_{2}\sqrt{1-\rho^2}} $$
하지만 식에서 규칙성이 보인다. $2\pi\sigma_{1}\sigma_{2}\sqrt{1-\rho^2}$에서 $1-\rho^2$부분은 $\mathbf{A}$가 달고 있던 상수항이다. 그리고 행렬부분의 행렬식이기도 하다. 여기서 중요한 힌트를 얻는다. $\exp()$안의 식은 아무튼 이차형식이고, 이차형식의 행렬을 잡는 방법은 이 외에도 많다. 그렇다면 $\exp()$ 밖의 식과 뭔가 연관이 있는 행렬을 잡으면 좋을 것이다.
그러므로 이제 $\exp()$ 밖의 상수항을 관찰해보도록 하자. $2\pi\sigma_{1}\sigma_{2}\sqrt{1-\rho^2}$에서 $2\pi$는 일변량 정규분포에도 있던 것이므로 우선 신경쓰지 않는다. 문제는 뒤의 $\sigma_{1}\sigma_{2}\sqrt{1-\rho^2}$인데, 루트는 다루기 힘드니까 우선 제곱하고, 나중에 다시 루트를 씌우는 방식으로 처리하자. 제곱한 것을 변형해보면, 어떤 행렬의 행렬식임을 알 수 있다.
$$ \sigma_{1}^2\sigma_{2}^2(1-\rho^2)=\sigma_{1}^2\sigma_{2}^2-\sigma_{1}^2\sigma_{2}^2\rho^2=\begin{vmatrix}\sigma_{1}^2&\rho\sigma_{1}\sigma_{2}\\\rho\sigma_{1}\sigma_{2}&\sigma_{2}^2\end{vmatrix} $$
행렬의 성분을 보면, 주대각선 성분은 각각 $X$와 $Y$의 분산이다. 그리고 나머지 성분은 $X$와 $Y$의 공분산이다. 분산은 사실 공분산의 특수한 경우임을 감안하면, 모든 성분은 공분산이다. 따라서 이 행렬은 공분산 행렬(Covariance Matrix; 协方差矩阵)이라고 부르며, $\mathbf{\Sigma}$로 나타낸다. 이제 이 사실을 이용해 상수를 간단히 하면
$$ f(x,y)=\frac{\exp\left[-\frac{1}{2}\mathbf{z^T}\mathbf{A}\mathbf{z}\right]}{2\pi\sqrt{\vert\mathbf{\Sigma}\vert}} $$
식은 간단해졌지만 이차형식의 행렬 $\mathbf{A}$와 공분산 행렬 $\mathbf{\Sigma}$가 매칭이 안 된다. 이차형식의 행렬도 공분산행렬과 뭔가 연관이 있다면 좋을 것 같다. 결국 다음과 같이 이차형식을 변형하는 문제를 생각해야 한다.
$$ \mathbf{z^T}\mathbf{A}\mathbf{z}=\mathbf{w^T}\mathbf{B}\mathbf{w},\space\mathbf{w}=?,\space\mathbf{B}=? $$
이 문제를 해결하기 위해 다음과 같은 두 가지 방법을 생각할 수 있다:
$\space$
(1) 적절한 선형변환 $\mathbf{z=Cw}$를 취하면, $\mathbf{z^T}\mathbf{Az}=\mathbf{(Cw)^T}\mathbf{A(Cw)}=\mathbf{w^T}\mathbf{(C^T}\mathbf{AC)w}$이므로 $\mathbf{B}=\mathbf{C^T}\mathbf{AC}$이다. $\mathbf{A}$는 이미 알고 있고 $\mathbf{B=\Sigma}$를 가정하면 $\mathbf{C}$를 구할 수 있다.
(2) 마찬가지로 $\mathbf{z=Cw}$를 가정하자. $\mathbf{B=\Sigma}$를 가정하지 않고 적절한 $\mathbf{C}$를 찾아보자. 그리고 $\mathbf{B}=\mathbf{C^T}\mathbf{AC}$를 이용해서 $\mathbf{B}$를 구한다. 이 경우 $\mathbf{B=\Sigma}$이거나 최소한 $\mathbf{\Sigma}$와 연관이 있기를 바랄 뿐이다.
$\space$
두 방법 중 (2)가 더 쉬워보인다. 최종 결과물인 행렬을 방정식을 통해 얻는 것이 아니라 그냥 차근차근 곱하면 되기 때문이다. 다만 방법 (2)를 택할 경우, $\mathbf{C}$의 경우의 수가 굉장히 다양해진다는 문제를 감안해야 한다.
현재 $\mathbf{z}$의 성분은 $\frac{x-\mu_1}{\sigma_1}$, $\frac{y-\mu_2}{\sigma_2}$이다. 먼저 $\mathbf{w}$를 정하고 이에 해당하는 선형변환을 얻어야 하는데, 우선 $\mathbf{w}=\begin{pmatrix}x-\mu_1\\y-\mu_2\end{pmatrix}$와 같이 변환 후의 벡터가 간단한 것을 가정하도록 한다.
이렇게 하면 선형변환의 행렬 $\mathbf{C}=\begin{pmatrix}1/\sigma_1&0\\0&1/\sigma_2\end{pmatrix}$이고, 이차형식의 행렬 $\mathbf{B}=\mathbf{\Sigma}^{-1}$을 얻는다. 정말 놀라운 사실이다.
$$ \begin{split} \mathbf{B}&=\frac{1}{1-\rho^2}\begin{pmatrix}1/\sigma_1&0\\0&1/\sigma_2\end{pmatrix}^T\begin{pmatrix}1&-\rho\\-\rho&1\end{pmatrix}\begin{pmatrix}1/\sigma_1&0\\0&1/\sigma_2\end{pmatrix} \\[2ex] &=\frac{1}{1-\rho^2}\begin{pmatrix}1/\sigma_1^2&-\rho/\sigma_1\sigma_2\\-\rho/\sigma_1\sigma_2&1/\sigma_2^2\end{pmatrix} \\[2ex] &=\frac{1}{(1-\rho^2)\sigma_1^2\sigma_2^2}\begin{pmatrix}\sigma_2^2&-\rho\sigma_1\sigma_2\\-\rho\sigma_1\sigma_2&\sigma_1^2\end{pmatrix} \\[2ex] &=\mathbf{\Sigma}^{-1} \end{split} $$
한편, $x$ 대신 $x_1$, $y$ 대신 $x_2$를 쓰면 $\mathbf{w}=\begin{pmatrix}x-\mu_1\\y-\mu_2\end{pmatrix}=\begin{pmatrix}x_1\\x_2\end{pmatrix}-\begin{pmatrix}\mu_1\\\mu_2\end{pmatrix}=\mathbf{x}-\boldsymbol{\mu}$로 나타낼 수 있으므로, 최종적으로 이변량 정규분포의 PDF의 형태를 위와 같이 정리할 수 있다.
#3. 이변량 정규분포의 성질
(1) $\iint_{\mathbb{R}^2}f(x,y)\space dxdy=1$, $f(x,y)\ge0$
$f(x,y)$가 확률밀도라면 당연히 만족해야 할 성질이다. 먼저 $f(x,y)$가 두 정규분포의 곱이므로 $f(x,y)\ge0$임을 쉽게 알 수 있다. 그리고 $\iint_{\mathbb{R}^2}f(x,y)\space dxdy$는 바로 계산하기 복잡하므로 다음과 같이 변환을 이용한다.
$$ \begin{split} &\begin{cases} u=\frac{x-\mu_1-\rho\frac{\sigma_1}{\sigma_2}(y-\mu_2)}{\sigma_1\sqrt{1-\rho^2}} \\ v=\frac{y-\mu_2}{\sigma_2} \end{cases} \\ &\vert J\vert=\begin{Vmatrix}x_u&x_v\\y_u&y_v\end{Vmatrix}=\begin{Vmatrix}\sigma_1\sqrt{1-\rho^2}&0\\0&\sigma_2\end{Vmatrix}=\sigma_1\sigma_2\sqrt{1-\rho^2},\space(\because \sigma_i>0) \\ &\vert J\vert f(u,v)=\frac{\exp\left(-\frac{u^2}{2}\right)}{\sqrt{2\pi}}\cdot\frac{\exp\left(-\frac{u^2}{2}\right)}{\sqrt{2\pi}}=\mathrm{N}(u;0,1)\cdot\mathrm{N}(v;0,1) \\[2ex] &\iint_{\mathbb{R}^2}f(x,y)\space dxdy=\iint_{\mathbb{R}^2}f(u,v)\vert J\vert\space dudv=1 \end{split} $$
(2) 이변량 정규분포의 주변분포, 조건부분포도 역시 정규분포이다.
이변량 정규분포를 두 정규분포의 곱으로 분해했으므로 주변분포는 구하기 쉽다. 먼저 $Y$의 주변분포 $f_Y(y)$를 구해보자.
$$ \begin{split} f_Y(y)&=\int_{\mathbb{R}}f(x,y)\space dx \\ &=\mathrm{N}(y;\mu_2,\sigma_2^2)\int_{\mathbb{R}}\mathrm{N}\left(x;\mu_1+\rho\frac{\sigma_1}{\sigma_2}(y-\mu_2),\sigma_1^2(1-\rho^2)\right)\space dx \\ &=\mathrm{N}(y;\mu_2,\sigma_2^2)\cdot1 \end{split} $$
같은 방식으로 $f_X(x)=\mathrm{N}(x;\mu_1,\sigma_1^2)$이다. 이 결과를 이용하여 계속해서 조건부 분포를 구해보자.
$$ \begin{split} &f_{X\mid Y}(x\mid y)=\frac{f(x,y)}{f_Y(y)}=\frac{\mathrm{N}\left(x;\mu_1+\rho\frac{\sigma_1}{\sigma_2}(y-\mu_2),\sigma_1^2(1-\rho^2)\right)\cdot\mathrm{N}(y;\mu_2,\sigma_2^2)}{\mathrm{N}(y;\mu_2,\sigma_2^2)} \\ &=\mathrm{N}\left(x;\mu_1+\rho\frac{\sigma_1}{\sigma_2}(y-\mu_2),\sigma_1^2(1-\rho^2)\right) \end{split} $$
같은 논리로 $f_{Y\mid X}(y\mid x)=\mathrm{N}\left(y;\mu_2+\rho\frac{\sigma_2}{\sigma_1}(x-\mu_1),\sigma_2^2(1-\rho^2)\right)$이다.
정리하면, $(X,Y)\sim\mathrm{N}(\mu_1,\mu_2,\sigma^2_1,\sigma_2^2,\rho)$일 때, 다음이 성립한다.
$$ \begin{split} &X\sim\mathrm{N}(\mu_1,\sigma_1^2),\space Y\sim\mathrm{N}(\mu_2,\sigma_2^2) \\ &(X\mid Y=y)\sim\mathrm{N}\left(\mu_1+\rho\frac{\sigma_1}{\sigma_2}(y-\mu_2),\sigma_1^2(1-\rho^2)\right) \\ &(Y\mid X=x)\sim\mathrm{N}\left(\mu_2+\rho\frac{\sigma_2}{\sigma_1}(x-\mu_1),\sigma_2^2(1-\rho^2)\right) \end{split} $$
(3) 이변량 정규분포에서는 최적선형예측이 곧 최적예측이다.
$(Y\mid X=x)\sim\mathrm{N}\left(\mu_2+\rho\frac{\sigma_2}{\sigma_1}(x-\mu_1),\sigma_2^2(1-\rho^2)\right)$이므로, 이변량 정규분포에서 $X=x$라는 조건 하에 $Y$의 기댓값과 분산은 다음과 같다.
$$ \begin{split} &\mathbb{E}(Y\mid X=x)=\mu_2+\rho\frac{\sigma_2}{\sigma_1}(x-\mu_1) \\ &\mathrm{Var}(Y\mid X=x)=\sigma_2^2(1-\rho^2) \end{split} $$
일반적으로 $X=x$가 주어질 때, $y$의 최적예측은 $\hat{y}(x):=\mathbb{E}(Y\mid X=x)$이다. 그리고 $g(x)=\mu_2+\rho\frac{\sigma_2}{\sigma_1}(x-\mu_1)$은 $y$의 최적선형예측이다. (평균제곱오차와 선형예측 참조.)
따라서 $X$와 $Y$가 이변량 정규분포를 따를 때, 최적예측과 최적선형예측이 일치한다. 이때 평균제곱오차가 최소화되고, 그 값은 $\mathrm{Var}(Y\mid X=x)=\sigma_2^2(1-\rho^2)$이다.
예측함수를 선형으로 가정하는 이유는 다루기 편해서이기도 하지만, 이변량 정규분포에서만큼은 선형함수가 바로 최적예측이어서 그렇게 안 하는게 더 이상하다는 결론이 나온다.
(4) 이변량 정규분포에서는 독립과 비상관이 동치이다. 즉, 독립이 비상관을 함축함은 물론이고 비상관도 독립을 함축한다.
어떤 분포이든 기본적으로 독립이 비상관을 함축하는 것은 당연하므로 여기서는 논의하지 않겠다. (공분산 참조.) 만약 이변량 정규분포를 결합분포로 가정하면, 비상관도 독립을 함축할 수 있게 된다.
비상관, 즉 $\rho=0$을 가정하자. 이때 $X$와 $(X\mid Y=y)$ 모두 $\mathrm{N}(\mu_1,\sigma_1^2)$을 따른다. 즉, $X$의 확률밀도는 $Y$의 관측값에 영향을 받지 않으므로 $X\perp Y$라고 할 수 있다.
이번에는 다른 관점으로 접근해보자. 두 확률변수가 독립이라는 것은 결합분포가 주변분포의 곱으로 분해된다는 것을 뜻한다. (조건부 분포 참조.) $f(x,y)$에 $\rho=0$을 대입하면 다음과 같이 식이 정리되고,
$$ f(x,y)=\mathrm{N}(x;\mu_1,\sigma_1^2)\cdot\mathrm{N}(y;\mu_2,\sigma_2^2) $$
$f_X(x)=\mathrm{N}(x;\mu_1,\sigma_1^2)$, $f_Y(y)=\mathrm{N}(y;\mu_2,\sigma_2^2)$이므로 $f(x,y)=f_X(x)f_Y(y)$이다.
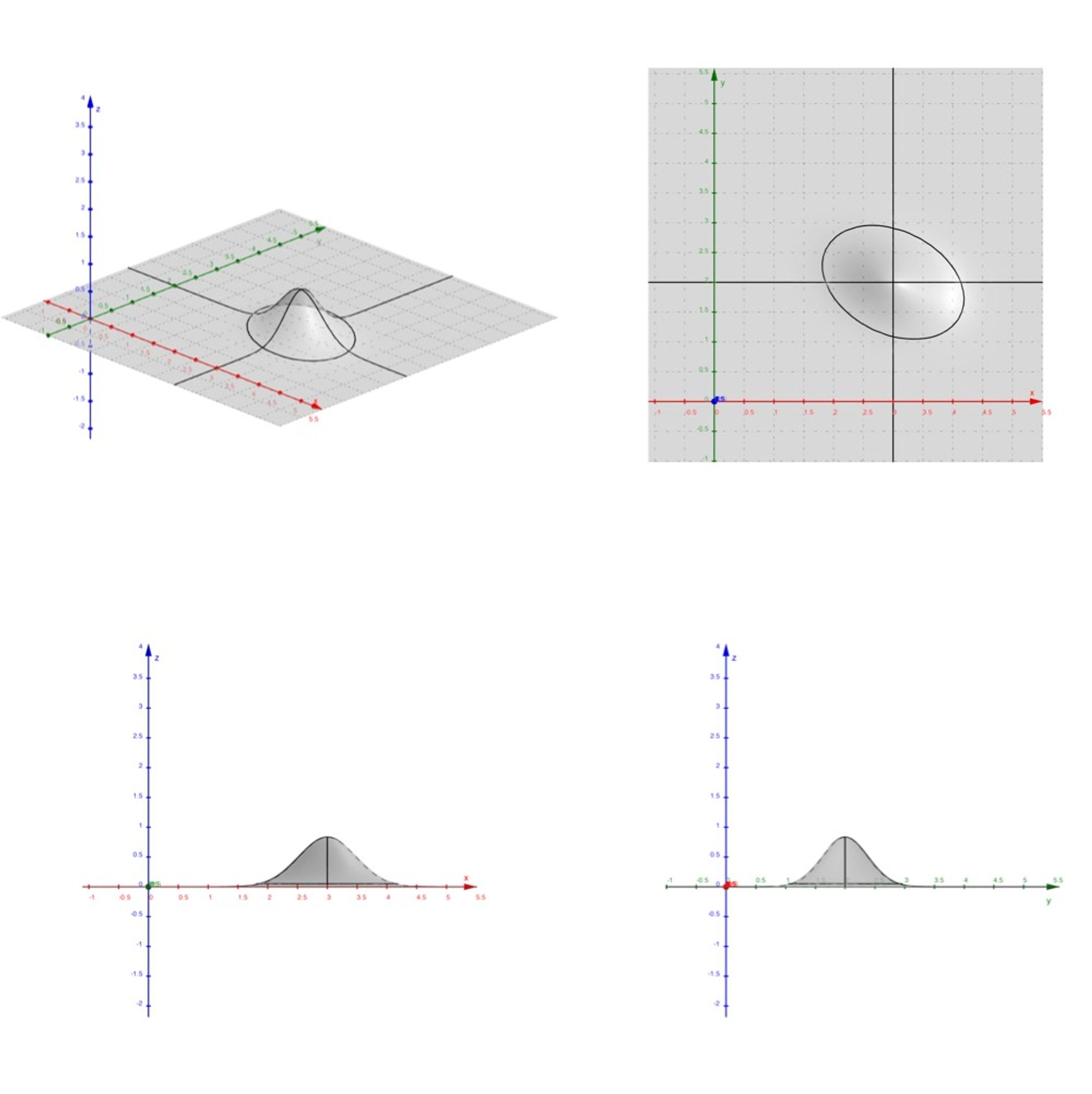
#4. 이변량 정규분포의 그래프
이차곡면을 연구할 때와 비슷하게, 이변량 정규분포의 그래프를 잘라서 연구해보자. (이차형식 참조.) 우선 가로로 잘라보자. $f(\mathbf{x;\boldsymbol{\mu},\Sigma})=\mathrm{constant}>0$로 두면 다음과 같이 이차곡선을 얻는다. ($\mathbf x=(x,y)^\mathbf T$로 둔다.)
$$ \mathbf{(x-\boldsymbol\mu)^T}\mathbf\Sigma^{-1}\mathbf{(x-\boldsymbol\mu)}=\mathrm{constant}>0 $$
이 이차곡선은 $xOy$에서 그려진 타원이며, 타원의 중심은 $\boldsymbol\mu=(\mu_1,\mu_2)$이다. 먼저 타원임을 보이기 위해, 좌변의 이차형식이 양의 정부호임을 보이자. $\mathbf\Sigma^{-1}$의 고유값을 계산하기보다는, $\mathbf{z^T}\mathbf{A}\mathbf{z}=\mathbf{(x-\boldsymbol\mu)^T}\mathbf\Sigma^{-1}\mathbf{(x-\boldsymbol\mu)}$이므로 $\mathbf A$의 고유값을 구하자.
한편, $\mathbf A=\frac{1}{1-\rho^2}\begin{pmatrix}1&-\rho\\-\rho&1\end{pmatrix}$이므로 $\mathbf B=\begin{pmatrix}1&-\rho\\-\rho&1\end{pmatrix}$의 고유값을 구하고 $\frac{1}{1-\rho^2}$를 곱한 것이 $\mathbf A$의 고유값이다.
$$ \vert\mathbf B-\lambda\mathbf I\vert=\begin{vmatrix}1-\lambda&-\rho\\-\rho&1-\lambda\end{vmatrix}=0\Rightarrow\lambda=1\pm\rho $$
이므로 $\mathbf A$의 고유값은 $\frac{1}{1-\rho^2}(1\pm\rho)$이다. $\rho$의 범위는 -1부터 +1사이이므로 두 고유값이 모두 양수임을 확인할 수 있다. 즉 $\mathbf{z\not=0}$에 대해 항상 $\mathbf{z^T}\mathbf{A}\mathbf{z}>0$이다. $\mathbf{z=0}$일 때, 즉 $\mathbf{X=\boldsymbol\mu}$일 때 $\mathbf{z^T}\mathbf{A}\mathbf{z}=0$이므로 그래프는 하나의 점이다. 따라서 가로로 자르면 그 단면은 점 $\boldsymbol\mu$를 중심으로 점점 퍼져나가는 타원이다.
이제 세로로 잘라보자. 세로로 자른다는 것은 $X=x$이거나 $Y=y$라는 조건을 정해주는 것이다. 앞서 밝혔듯 정규분포의 조건부 분포는 정규분포이다. 따라서 세로로 자르면 그 단면은 정규분포의 곡선이다.
이 정보들을 토대로 이변량 정규분포의 그래프를 그릴 수 있다.