지난 글에서 공분산이 0임을 비상관으로 정의했다. ‘비상관’은 문자 그대로 서로 관련이 없음을 의미한다. 그렇다면 공분산이 0이 아닌 다른 값이면 두 확률변수는 서로 관련이 있다는 것이다. 그리고 기왕이면 공분산의 절대값이 커질 수록 두 변수 사이의 관련성이 커지면 좋겠다.
이는 공분산으로 두 변수 간의 상관성을 측정하려는 시도라고 볼 수 있다. 그런데 이렇게 하면 문제가 하나 있는데, 변수의 단위가 달라진다는 데 있다. 공분산은 분산의 일반화이므로 분산과 같은 문제점을 안고 있는 것이다.
분산의 경우, 루트를 씌워 표준편차를 정의하여 해결했다. 하지만 영국의 수학자 칼 피어슨(Karl Pearson)은 다른 방식으로 이 문제를 해결했다. 바로 다음과 같이 $X$와 $Y$의 상관계수(Correlation Coefficient; 相关系数) $R(X,Y)$를 정의하는 것이다.
$$ R(X,Y):=\frac{\mathrm{Cov}(X,Y)}{\sqrt{\mathrm{Var}(X)}\sqrt{\mathrm{Var}(Y)}}=\frac{\mathrm{Cov}(X,Y)}{\mathrm{SD}(X)\mathrm{SD}(Y)} $$
이렇게 정의한 상관계수를 정의자의 이름을 따서 피어슨 상관계수(Pearson Correlation Coefficient, PCC; 皮尔逊相关系数)이라고 하며, 흔히 상관계수라 함은 바로 이 피어슨 상관계수를 의미한다.
피어슨 상관계수를 $R(X^{\ast},Y^{\ast})$와 같이 표준화된 변수를 통해 계산하는 것으로 정의하기도 하는데, 아래와 같이 $R(X^{\ast},Y^{\ast})=R(X,Y)$임을 보일 수 있기 때문에 문제되지 않는다. (표준화된 변수의 분산이 1임을 이용한다.)
$$ \begin{split} R(X^{\ast},Y^{\ast})&=\frac{\mathrm{Cov}\left(\frac{X-\mathbb{E}(X)}{\sqrt{\mathrm{Var}(X)}},\frac{Y-\mathbb{E}(Y)}{\sqrt{\mathrm{Var}(Y)}}\right)}{1\cdot1}=\frac{\mathrm{Cov}(X-\mathbb{E}(X),Y-\mathbb{E}(Y))}{\sqrt{\mathrm{Var}(X)}\sqrt{\mathrm{Var}(Y)}} \\ &=\frac{\mathrm{Cov}(X,Y)}{\sqrt{\mathrm{Var}(X)}\sqrt{\mathrm{Var}(Y)}}=R(X,Y) \end{split} $$
note1: 실제 통계분석에서는 여러가지 이유로(예를 들어 분류분석에서 마할라노비스 거리를 이용하기 위해) 먼저 변수를 표준화하는 과정을 거친 뒤 분석에 착수하는 경우가 많은데, 상관계수가 표준화 전후와 관계 없이 같은 값이라는 사실은 행운이다.
note2: 이 결과를 일반화하면 $\vert R(aX+b,cY+d)\vert=\vert R(X,Y)\vert$, 즉 데이터에 선형변환을 하더라도 상관계수의 부호는 바뀔지 몰라도 크기는 불변이다.
피어슨 상관계수는 공분산이 0일 때 0이다. 그리고 변수의 단위가 약분되어 사라지므로 골치 아픈 문제가 하나 해결된다. 이 외에도 하나 더 좋은 점이 있는데, 바로 상관계수의 범위가 -1부터 +1까지라는 것이다.
$$ \begin{split} &\mathrm{Var}\left(\frac{X}{\mathrm{SD}(X)}\pm\frac{Y}{\mathrm{SD}(Y)}\right)=\frac{\mathrm{Var}(X)}{[\mathrm{SD}(X)]^2}+\frac{\mathrm{Var}(Y)}{[\mathrm{SD}(Y)]^2}\pm2\frac{\mathrm{Cov}(X,Y)}{\mathrm{SD}(X)\mathrm{SD}(Y)} \\ &=2\pm2R(X,Y))\ge0 \\ &\therefore -1\le R(X,Y)\le1 \end{split} $$
상관계수가 0의 값을 가진다는 것은 곧 비상관을 의미한다. 그렇다면 양극단의 값인 -1이나 +1일 때는 무슨 의미일까? 우선 다음이 성립한다.
$$ R(X,Y)=+1\Rightarrow\mathrm{Var}\left(\frac{X}{\mathrm{SD}(X)}-\frac{Y}{\mathrm{SD}(Y)}\right)=2-(+2)=0 \\ R(X,Y)=-1\Rightarrow\mathrm{Var}\left(\frac{X}{\mathrm{SD}(X)}+\frac{Y}{\mathrm{SD}(Y)}\right)=2+(-2)=0 $$
그리고 어떤 확률변수의 분산이 0인 것은 그 확률변수가 사실은 상수임을 의미한다. 따라서
$$ R(X,Y)=+1\Rightarrow\frac{X}{\mathrm{SD}(X)}-\frac{Y}{\mathrm{SD}(Y)}=\mathrm{constant}\Rightarrow Y=aX+b(a>0) \\ R(X,Y)=-1\Rightarrow\frac{X}{\mathrm{SD}(X)}+\frac{Y}{\mathrm{SD}(Y)}=\mathrm{constant}\Rightarrow Y=aX+b(a<0) $$
즉, $\mathbb{R}^2$에서 상관계수가 +1이면 $(X,Y)$는 기울기가 양인 직선을 나타내고, 이것을 완벽한(Perfect; 完全) 양의(Positive; 正) 상관관계(Correlation; 相关)라고 한다. 상관계수가 -1이면 $(X,Y)$는 기울기가 음인 직선을 나타내고, 이것을 완벽한 음의(Negative; 负) 상관관계라고 한다. 아무튼 직선을 나타내므로, 완벽한 상관관계를 두고 선형관계(Linear Relation; 线性关系)라고도 한다.
한편, $Y=aX+b(a\not=0)$와 같이 먼저 두 확률변수 간의 선형관계를 가정했을 때 다음과 같은 결론을 얻는다. ($X$와 상수 $b$가 독립임을 기억하자.)
$$ \begin{split} &\mathrm{Cov}(X,Y)=\mathrm{Cov}(X,aX+b)=a\mathrm{Cov}(X,X)+\mathrm{Cov}(X,b)=a\mathrm{Var}(X) \\ &\mathrm{Var}(Y)=\mathrm{Var}(aX+b)=a^2\mathrm{Var}(X) \\ &\therefore R(X,Y)=\frac{a\mathrm{Var}(X)}{\sqrt{\mathrm{Var}(X)}\sqrt{a^2\mathrm{Var}(X)}}=\frac{a}{\vert a\vert}=\pm1 \end{split} $$
따라서 두 변수 사이에 선형관계가 존재한다는 것은 상관계수의 절댓값이 1인 것과 동치이다.
$$ Y=aX+b(a\not=0)\Leftrightarrow\vert R(X,Y)\vert=1 $$
#2. Python으로 상관계수 구하기
두 확률변수의 관측값을 알고 있다면 Python의 pandas 모듈로 상관계수를 쉽게 구할 수 있다. 어떤 사람의 한 달 소득 $Y$와 소비 $C$의 관련성을 알아보기 위해 상관계수 $R(Y,C)$를 구해보자. 우선 다음과 같은 코드를 실행시킨다.
import pandas as pd
y = [100, 300, 700, 200, 1000, 600, 500, 450, 270, 350]
c = [138, 328, 281, 165, 550, 350, 303, 220, 330, 280]
data = [[y[i]] + [c[i]] for i in range(min(len(y), len(c)))]
data = pd.DataFrame(data, columns=["Y", "C"])
print("관측값\\n", data)
print("\\n상관계수\\n", data.corr())
결과는 다음과 같이 $2\times2$행렬의 형태로 나온다. 이를 상관행렬(Correlation Matrix; 相关矩阵)이라고 한다.
관측값
Y C
0 100 138
1 300 328
2 700 281
3 200 165
4 1000 550
5 600 350
6 500 303
7 450 220
8 270 330
9 350 280
상관계수
Y C
Y 1.000000 0.811832
C 0.811832 1.000000
상관행렬의 성분은 모두 상관계수이다. 제1행 제1열의 성분은 1.00인데, 이는 $R(Y,Y)=1$이라는 뜻으로 해석한다. 제2행 제1열의 성분은 0.81인데, 이는 $R(Y,C)=0.81$라는 뜻이다. 상관계수가 0.81이면 두 변수 간 강한 양의 상관관계가 있다는 의미이다. 따라서 ‘한 사람의 한 달 소득과 소비는 강한 양의 상관관계를 가진다’라는 결론을 얻는다.
note1: ‘소득이 많으면 소비도 많이한다’는 식으로 해석할 수는 없다. 소득과 소비 중 어느 것이 원인이고 결과인지 알 수 없기 때문에, ‘소비를 많이 하면 소득도 많다’라고 반대로 해석할 수도 있기 때문이다. 이를 두고 흔히 상관분석(Correlation Analysis; 相关分析)은 상관관계를 발견할 뿐이고 인과관계를 발견할 수 없다고 표현한다. 인과관계는 회귀분석(Regression Analysis; 回归分析)을 통해 발견할 수 있다.
note2: 사실 상관계수를 구하는 것만으로는 완벽한 상관분석이라 할 수 없고, 보통 통계적 유의성(Statistical Significance; 显著性)을 검정하는 과정을 거쳐야 한다. 추후 작성예정.
상관행렬은 항상 주대각선의 성분이 1인 대칭행렬이다. 상관계수의 정의에 의해 임의의 확률변수 $X$와 $Y$에 대해 항상 $R(X,X)=1$이고 $R(X,Y)=R(Y,X)$이 성립하기 때문이다.
위 데이터에 새로운 변수인 연령 $A$를 추가해서 상관계수를 구해보자.
import pandas as pd
y = [100, 300, 700, 200, 1000, 600, 500, 450, 270, 350]
c = [138, 328, 281, 165, 550, 350, 303, 220, 330, 280]
a = [27, 25, 48, 69, 46, 31, 37, 72, 21, 25]
data = [[y[i]] + [c[i]] + [a[i]] for i in range(min(len(y), len(c), len(a)))]
data = pd.DataFrame(data, columns=["Y", "C", "A"])
print("관측값\\n", data)
print("\\n상관계수\\n", data.corr())
결과는 다음과 같다.
관측값
Y C A
0 100 138 27
1 300 328 25
2 700 281 48
3 200 165 69
4 1000 550 46
5 600 350 31
6 500 303 37
7 450 220 72
8 270 330 21
9 350 280 25
상관계수
Y C A
Y 1.000000 0.811832 0.187744
C 0.811832 1.000000 -0.220045
A 0.187744 -0.220045 1.000000
우선, $R(Y,C)=R(C,Y)=0.81$로 같다. 새로운 변수를 추가하더라도 원래의 상관관계에는 영향이 없다. 그리고 $C$와 $A$, $Y$와 $A$모두 상관관계가 약한 것으로 드러났다. 한편, 주대각선의 성분은 모두 1이며, 상관행렬은 대칭행렬이다.
#3. Python으로 상관계수 시각화하기
#3.1 산점도와 회귀선
<hide/>
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
# 데이터 입력
y = [100, 300, 700, 200, 1000, 600, 500, 450, 270, 350]
c = [138, 328, 281, 165, 550, 350, 303, 220, 330, 280]
a = [27, 25, 48, 69, 46, 31, 37, 72, 21, 25]
variables = [y, c, a]
variables_name = ["Y", "C", "A"]
# 데이터 프레임 생성
data = [[y[i]] + [c[i]] + [a[i]] for i in range(min(len(y), len(c), len(a)))]
data = pd.DataFrame(
data, columns=[variables_name[i] for i in range(len(variables_name))]
)
# 데이터, 상관계수 출력
print("관측값\n", data)
print("\n상관계수\n", data.corr())
# 3x3 산점도 그리기
fig, ax = plt.subplots(3, 3, layout="constrained")
for i in range(len(variables)):
for j in range(len(variables)):
# 산점도 그리기
ax[i, j].scatter(variables[i], variables[j], color="#000")
# 회귀선 그리기
linear_model = np.polyfit(variables[i], variables[j], 1)
linear_model = np.poly1d(linear_model)
ax[i, j].plot(variables[i], linear_model(variables[i]), color="r")
# 상관계수 계산, 제목에 넣기
r = data[variables_name[i]].corr(data[variables_name[j]])
title = (
"R(%s" % variables_name[i]
+ ",%s) =" % variables_name[j]
+ " %s" % round(r, 3)
)
ax[i, j].set_title(title)
# 이미지 저장
fig.set_size_inches(10, 10)
fig.savefig("Correlation Scatter Plot")
#3.2 히트맵
<hide/>
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 데이터 입력
y = [100, 300, 700, 200, 1000, 600, 500, 450, 270, 350]
c = [138, 328, 281, 165, 550, 350, 303, 220, 330, 280]
a = [27, 25, 48, 69, 46, 31, 37, 72, 21, 25]
variables_name = ["Y", "C", "A"]
# 데이터 프레임 생성
data = [[y[i]] + [c[i]] + [a[i]] for i in range(min(len(y), len(c), len(a)))]
data = pd.DataFrame(
data, columns=[variables_name[i] for i in range(len(variables_name))]
)
# 데이터, 상관계수 출력
print("관측값\n", data)
print("\n상관계수\n", data.corr())
# 3x3 히트맵 그리기
plt.figure(figsize=(10, 10))
color = sns.color_palette("Spectral", as_cmap=True)
heatmap = sns.heatmap(
data.corr(), vmin=-1, vmax=1, annot=True, cmap=color, linewidths=0.5
)
# 이미지 저장
plt.savefig("Correlation Heatmap")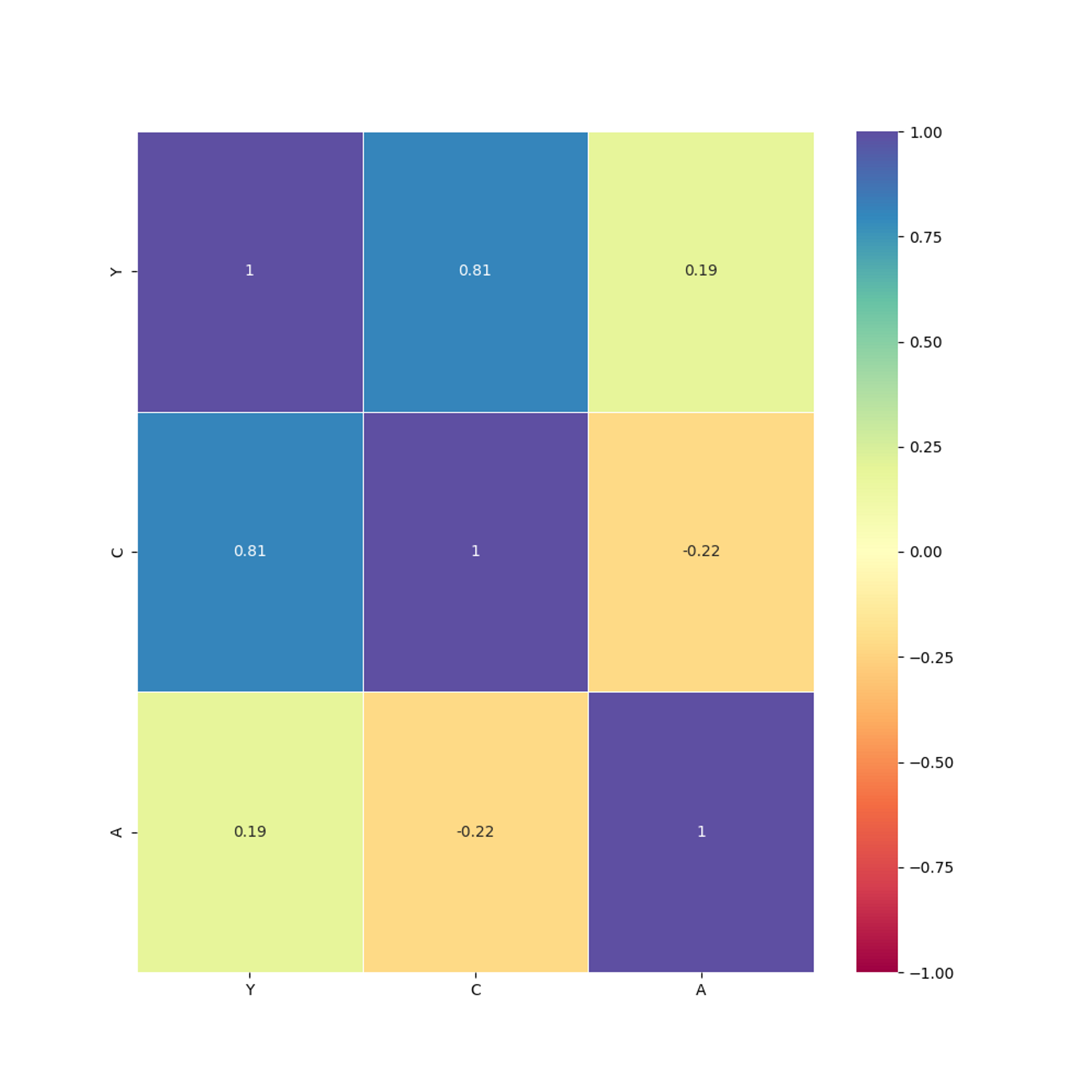
'Mathematics' 카테고리의 다른 글
| 평균제곱오차와 선형예측 (0) | 2023.01.11 |
|---|---|
| 이변량 정규분포 (0) | 2023.01.09 |
| 공분산 (0) | 2023.01.01 |
| 분산과 표준편차 (0) | 2022.12.28 |
| 평균과 기댓값 (0) | 2022.12.27 |


