#1. 분산과 공분산
분산의 성질을 되짚어 보자. 확률변수 $X_i$의 선형합 $\sum_{i=1}^{n}a_iX_i$의 분산은 다음과 같이 구한다.
$$
\mathrm{Var}\left(\sum_{i=1}^{n}a_iX_i\right)=\sum_{i=1}^{n}a_i^2\mathrm{Var}(X_i)+\sum_{i\not=j}a_ia_j\mathbb{E}\lbrack (X_i-\mathbb{E}(X_i))(X_j-\mathbb{E}(X_j)) \rbrack
$$
분산의 정의에 의해, 이 식에서 $\mathrm{Var}(X_i)=\mathbb{E}\lbrack (X_i-\mathbb{E}(X_i))(X_i-\mathbb{E}(X_i)) \rbrack$이다. 즉, 선형합의 분산을 전개할 때, 인덱스가 같은 것의 기댓값은 분산으로 처리했고, 다른 것의 기댓값은 따로 뺐음을 알 수 있다.
이제 인덱스가 다른 것의 기댓값을 정의하기 위해 공분산(Covariance; 协方差)이라는 것을 정의해보자. 서로 다른 확률변수 $X$와 $Y$의 공분산 $\mathrm{Cov}(X,Y)$는 다음과 같이 정의된다.
$$
\mathrm{Cov}(X,Y):=\mathbb{E}[(X-\mathbb{E}(X))(Y-\mathbb{E}(Y))]
$$
정의에 의해 $\mathrm{Cov}(X,X)=\mathrm{Var}(X)$이다. 즉, $X$의 분산은 $X$와 $X$의 공분산으로 일반화 할 수 있다. 이제 공분산을 이용하여 선형합의 분산을 전개해보자. 아래와 같이 깔끔하게 공식을 고칠 수 있다.
$$
\mathrm{Var}\left(\sum_{i=1}^{n}a_iX_i\right)=\sum_{i,j=1}^{n}a_ia_j\mathrm{Cov}(X_i,X_j)
$$
예를 들어 $n=3$을 가정하면 다음과 같이 전개된다.
$$
\begin{split}
&\mathrm{Var}(a_1X_1+a_2X_2+a_3X_3)
\\
&=a_1a_1\mathrm{Cov}(X_1,X_1)+a_1a_2\mathrm{Cov}(X_1,X_2)+a_1a_3\mathrm{Cov}(X_1,X_3)
\\
&+a_2a_1\mathrm{Cov}(X_2,X_1)+a_2a_2\mathrm{Cov}(X_2,X_2)+a_2a_3\mathrm{Cov}(X_2,X_3)
\\
&+a_3a_1\mathrm{Cov}(X_3,X_1)+a_3a_2\mathrm{Cov}(X_3,X_2)+a_3a_3\mathrm{Cov}(X_3,X_3)
\end{split}
$$
그리고 $a_ia_j\mathrm{Cov}(X_i,X_j)=a_ja_i\mathrm{Cov}(X_j,X_i)$임이 자명하므로 다음과 같은 공식도 얻을 수 있다.
$$
\mathrm{Var}\left(\sum_{i=1}^{n}a_iX_i\right)=\sum_{i=1}^{n}a_i^2\mathrm{Var}(X_i)+2\sum_{i<j}^{n}a_ia_j\mathrm{Cov}(X_i,X_j)
$$
#2. 독립과 비상관
공분산의 의미를 알아보기 위해 $\mathrm{Cov}(X,Y)$를 변형해보자.
$$ \begin{split} \mathrm{Cov}(X,Y)&:=\mathbb{E}[(X-\mathbb{E}(X))(Y-\mathbb{E}(Y))] \\ &=\mathbb{E}[XY-X\mathbb{E}(Y)-Y\mathbb{E}(X)+\mathbb{E}(X)\mathbb{E}(Y)] \\ &=\mathbb{E}[XY]-\mathbb{E}[X\mathbb{E}(Y)]-\mathbb{E}[Y\mathbb{E}(X)]+\mathbb{E}[\mathbb{E}(X)\mathbb{E}(Y)] \\ &=\mathbb{E}[XY]-\mathbb{E}(Y)\mathbb{E}[X]-\mathbb{E}(X)\mathbb{E}[Y]+\mathbb{E}(X)\mathbb{E}(Y) \\ &=\mathbb{E}(XY)-\mathbb{E}(X)\mathbb{E}(Y) \end{split} $$
여기서 만약 $X$와 $Y$가 독립이라면 $\mathbb{E}(XY)=\mathbb{E}(X)\mathbb{E}(Y)$이다. 따라서 다음과 같은 결과를 얻는다.
$$ X\perp Y\Rightarrow\mathrm{Cov}(X,Y)=0 $$
이 명제의 역은 성립하지 않는다. $\mathbb{E}(XY)=\mathbb{E}(X)\mathbb{E}(Y)$이라고 해서 반드시 $X$와 $Y$의 독립을 보장하지는 않기 때문이다. $X$와 $Y$가 독립이 아니지만 공분산이 0인 경우가 존재한다. 예를 들어 $X$와 $Y$의 관측값이 단위원 $x^2+y^2=1$에 균등하게 분포하고 있다고 가정해보자.
만약 $x=1$일 경우 $y=0$이다. $x=1/2$일 경우 $y=\pm\sqrt{3/4}$이다. $x=1/4$일 경우 $y=\pm\sqrt{15/16}$이다. 이것을 일반화 해서 $x=x_0$에 대해 $y=\pm\sqrt{1-x_0^2}$이다. 즉, $x$가 어떤 값이든지 $y$의 관측값은 0이거나 한 쌍의 반수(Opposite Number; 相反数)이다. 그러므로 $y$의 관측값의 합은 항상 0이된다.
그리고 $y$가 균등하게 분포하고 있다고 가정했으므로 이 두가지의 값을 가질 확률은 0.5로 같다. 그래서 임의의 $x$에 대해 $\mathbb{E}(Y\mid X=x)$를 계산해보면 항상 0이고, 같은 논리로 모든 $y$에 대해 $\mathbb{E}(X\mid Y=y)=0$이다.
$$ \mathbb{E}(Y\mid X=x)=0.5\cdot\left(-\sqrt{1-x^2}\right)+0.5\cdot\left(+\sqrt{1-x^2}\right)=0 $$
이번에는 $X=x$라는 조건이 없다고 하고 $\mathbb{E}(Y)$를 구해보자. 이 경우 $Y$의 관측값은 0이거나 여러쌍의 반수이다. 결국 기댓값을 구하는 도중 반수끼리 상쇄되어 0이 될 것이다. 따라서 다음과 같이 $\mathrm{Cov}(X,Y)=0$임을 유도할 수 있다.
$$ \begin{split} &\mathbb{E}(XY)=\mathbb{E}[\mathbb{E}(XY\mid X=x)]=\mathbb{E}[x\cdot\mathbb{E}(Y\mid X=x)]=\mathbb{E}[x\cdot 0]=0 \\ &\mathbb{E}(X)\mathbb{E}(Y)=0\cdot 0=0 \\ &\therefore \mathrm{Cov}(X,Y)=\mathbb{E}(XY)-\mathbb{E}(X)\mathbb{E}(Y)=0-0=0 \end{split} $$
공분산은 0이다. 하지만 $X$와 $Y$는 결코 독립이라고 할 수 없다. $X^2+Y^2=1$이라는 아주 명확한 관계가 있다. 위와 같은 반례를 통해 공분산이 0이라는 사실이 두 확률변수의 ‘독립’을 의미하지는 않는다는 사실을 알 수 있다.
하지만 공분산이 0이라는 사실은 분명 의미가 있다. 이것을 비상관(Uncorrelated; 不相关)이라고 정의한다. 즉, 비상관의 정의는 ‘공분산이 0’으로 할 수 있고, 독립의 정의는 ‘결합분포를 주변분포의 곱으로 나타낼 수 있음’으로 하며, ‘독립은 비상관을 함축하지만 비상관은 그렇지 못하다’라고 요약할 수 있다.
$$
\begin{split}
&독립\Leftrightarrow f(x,y)=f_X(x)f_Y(y)
\\
&비상관\Leftrightarrow \mathrm{Cov}(X,Y)=0
\\
&독립\Rightarrow비상관
\end{split}
$$
$\space$
TFAE.
(1) $\mathrm{Cov}(X,Y)=0$
(2) $\mathbb{E}(XY)=\mathbb{E}(X)\mathbb{E}(Y)$
(3) $\mathrm{Var}(X\pm Y)=\mathrm{Var}(X)+\mathrm{Var}(Y)$
$\space$
note: 공분산이 0임을 ‘비상관’이라고 하는 이유는 ‘상관계수’라는 개념과 관련이 있다. 추후 작성 예정.
#3. 공분산의 성질
공분산이 포함된 식을 정리할 때 쓰는 성질들을 요약해둔다.
(1) $\mathrm{Cov}(X,X)=\mathrm{Var}(X)$
(2) $\mathrm{Cov}(X,Y)=\mathrm{Cov}(Y,X)$
(3) $\mathrm{Cov}(aX,bY)=ab\mathrm{Cov}(X,Y)$
(1)과 (2)는 공분산의 정의에 의해 당연히 성립하는 식이다. (2)는 공분산의 대칭성이라고 부른다. (3)은 기댓값의 선형성에 의해 성립한다.
선형합의 분산처럼 선형합의 공분산 역시 공식이 있다.
(4) $\mathrm{Cov}(\sum_{i=1}^{n}a_iX_i,\sum_{j=1}^{m}b_jY_j)=\sum_{i=1}^{n}\sum_{j=1}^ma_ib_j\mathrm{Cov}(X_i,Y_j)$
예를 들어, $(n,m)=(2,2)$의 경우 공분산을 전개했을 때 다음과 같이 $2\times2=4$개의 항이 있을 것이고
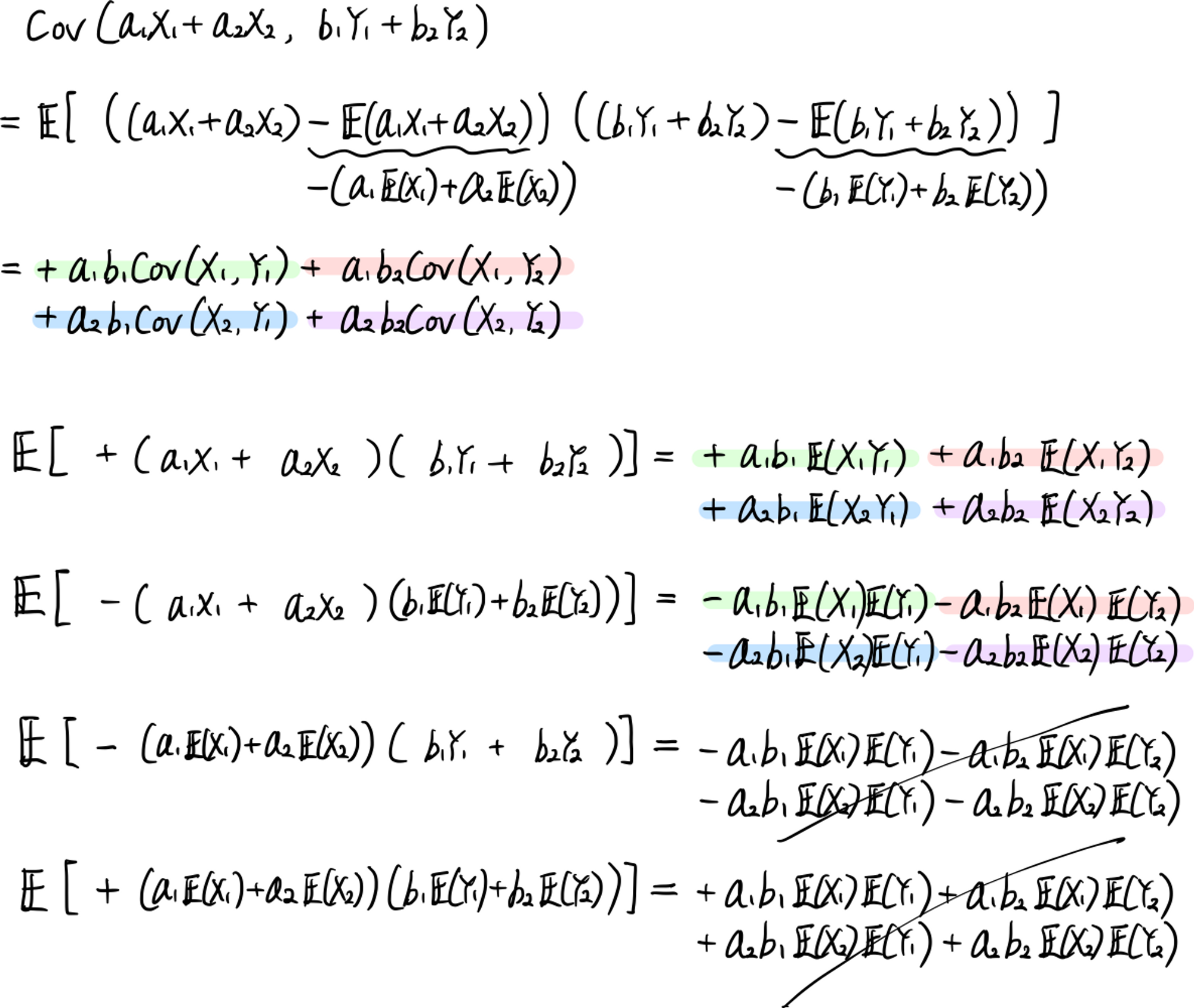
$(n,m)=(2,1)$의 경우 다음과 같이 $2\times1=2$개의 항이 있을 것이다.
$$
\mathrm{Cov}(a_1X_1+a_2X_2,b_1Y_1)=a_1b_1\mathrm{Cov}(X_1,Y_1)+a_2b_1\mathrm{Cov}(X_2,Y_1)
$$



