#1. 삼점추정과 삼각분포
어떤 확률변수가 있는데 그것의 자세한 분포를 모를 때, 흔히 삼점추정(Three-point Estimation; 三点估计)으로 해결하곤 한다. 삼점이란, 관측값의 최소, 최대, 최빈값을 의미한다. 즉, 확률변수가 가질 수 있는 양극단의 값 $a$, $b$와 가장 많이 등장하는 관측값 $c$로 분포를 묘사하는 것이다.
note: 예를 들어, 가게의 한 달 매출 $X$가 $x$이상일 확률을 추정하고 싶을 때, 우선 과거의 경험에 비추어 $X$의 범위를 설정한다. 여기서 $a$와 $b$가 결정된다. 그리고 최고봉에서 매출이 얼마나 나왔는지에 따라 $c$가 결정된다. 그러면 $P(X\ge x)=1-P(X<x)$이고, $P(X<x)=\int_{-\infty}^{x}f_X(x;a,b,c)\space dx$이므로 원하는 확률을 추정할 수 있게 된다.
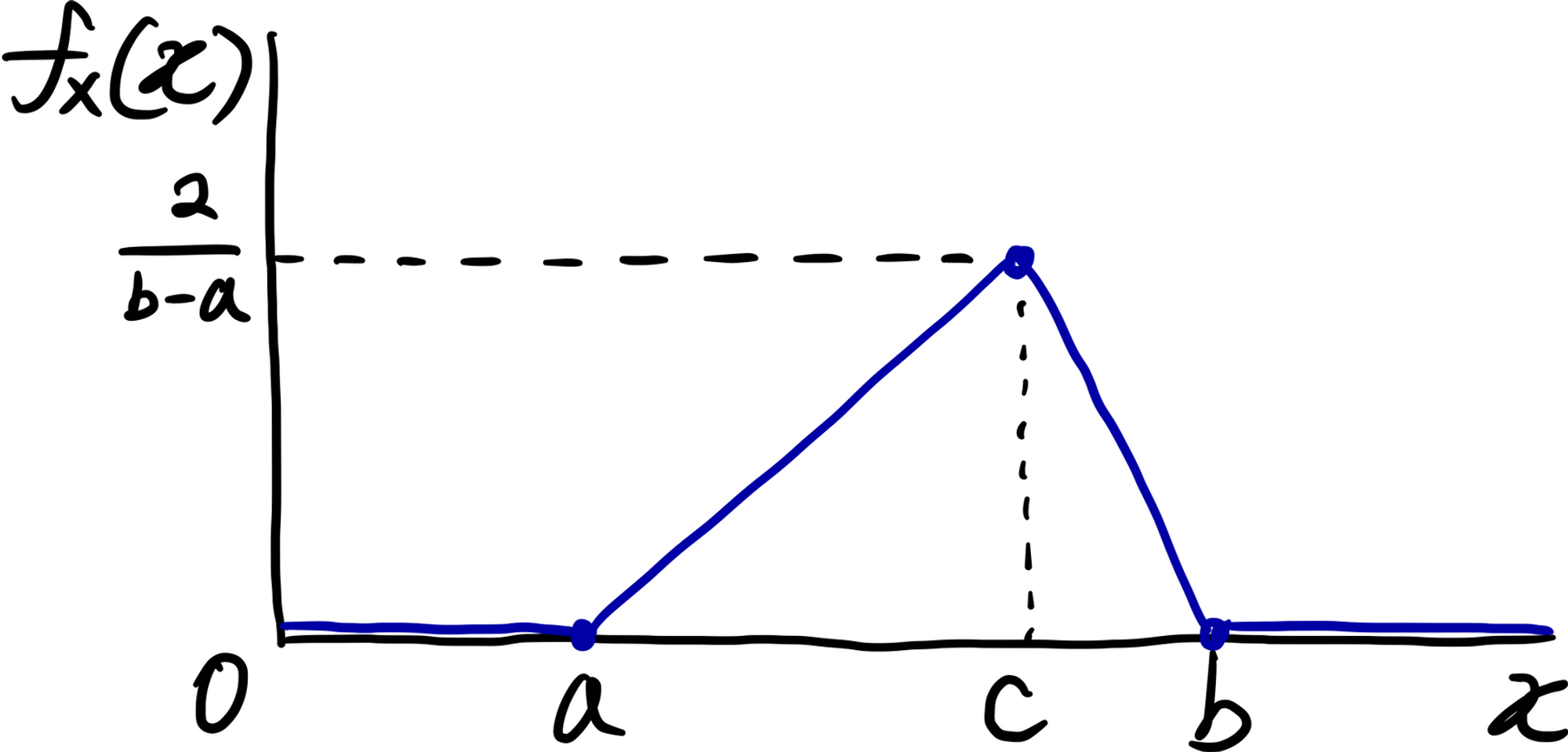
위 그림은 삼점추정에 의해 그려진 그래프로, 이러한 그래프를 갖는 분포를 삼각분포(Triangular Distribution; 三角分布)라고 한다. 삼각분포의 기호는 따로 없고, 확률밀도는 다음과 같이 주어진다.
$$
f_X(x;a,b,c)=
\begin{cases}
\frac{2}{b-a}\cdot\frac{x-a}{c-a},&a\le x<c
\\
\frac{2}{b-a},&x=c
\\
\frac{2}{b-a}\cdot\frac{b-x}{b-c},&c<x\le b
\\
0,&\mathrm{otherwise}
\end{cases}
$$
식이 복잡해보이지만 늘 그래왔듯이 직접 유도하면 전혀 복잡하지 않다. 핵심은 PDF아래 면적이 1임을 이용하는 것이다. 이것도 자주 써왔던 테크닉이다.

#2. 대칭삼각분포와 균등분포의 합성곱
한편, 최빈값 $c$가 구간 $[a,b]$의 정중앙에 위치하면, 다시말해 $c=\frac{a+b}{2}$이면 삼각분포는 직선 $x=c$에 관해 대칭이며, 이를 대칭삼각분포(Symmetric Triangular Distribution; 对称三角分布)라고 한다. 대칭삼각분포는 대칭성 외에도 아주 중요하고 재미있는 성질이 하나 있는데, 바로 두 균등분포의 합성곱으로 나타낼 수 있다는 것이다.
이 사실을 보이기 위해, 먼저 ‘두 주사위 눈의 합이…일 확률을 구하는 문제’를 생각해보자. 이 문제는 기초수학에서 흔히 등장하는 단순한 문제이지만 아주 심오한 뜻을 담고있다. 두 주사위의 눈을 각각 확률변수 $X$와 $Y$로 두고, 그것의 합을 $Z=X+Y$라고 하자.
$X$는 1부터 6까지의 값을 같은 가능성으로 갖는다. 따라서 $X\sim\mathrm{U}[1,6]$이라고 할 수 있다. 본래 균등분포는 연속확률변수에 대해서 정의되는 것이지만, 사실 이렇게 이산적인 균등분포를 정의해도 아무런 문제가 없다. 같은 방식으로 $Y\sim\mathrm{U}[1,6]$이다. 그렇다면 합성곱의 정의에 의해 다음이 성립한다.
$$
Z=X+Y\sim\mathrm{U}[1,6]\ast\mathrm{U}[1,6]
$$
확률질량함수 $f_Z(z)$를 구해보자. 직접 $X$와 $Y$를 나열하고, 그것의 합 $Z$를 계산하여 나열한다. $Z$는 36개의 값을 가진다. 그런데 과연 이 36개의 값이 같은 빈도로 나왔을까? 아니다. 분명히 7이라는 숫자가 6회로 가장 많고, 그 다음은 6과 8이 각각 5회의 빈도로 등장한다. 그 다음으로는 5와 9이고, 총 4회 등장한다. 이런식으로 세다 보면, 2와 12가 각각 1회씩 등장하는 것으로 마무리된다. 이제 이 사실을 다음과 같이 보기 좋게 정리해보자.

그림을 보면, $Z$의 분포는 대칭삼각분포임을 알 수 있다. 한편, 구간을 바꾸어 $\mathrm{U}[1,4]$와 $\mathrm{U}[2,5]$의 합성곱을 구해도 여전히 대칭삼각분포이다.
#3. 사다리꼴 분포
그렇다면 임의의 두 균등분포를 합성곱하면 대칭삼각분포를 얻을 수 있을까? 다음 그림을 보면 그렇지 않다라는 사실을 알 수 있다.

이렇게 생긴 분포는 사다리꼴 분포(Trapezoidal Distribution; 梯形分布)라고 하며, 여기서는 그중에서도 특수한 대칭사다리꼴 분포를 얻었다. 대칭삼각분포와 다른 이유는, 합성곱을 이루는 두 균등분포의 ‘구간의 길이가 다르다’는 데 있다.
다시 말해 두 균등분포를 합성곱할 때, 구간의 길이가 같다면 대칭삼각분포를 얻고, 다르다면 대칭사다리꼴분포를 얻는다. 또 하나 중요한 사실은 항상 대칭인 분포를 얻는다는 것이다.
일반적인 사다리꼴 분포의 PDF도 삼각분포와 비슷한 방식으로 구할 수 있다.
$$
f_X(x;a,b,c,d)=
\begin{cases}
\frac{2}{b-a+d-c}\cdot\frac{x-a}{c-a},&a\le x<c
\\
\frac{2}{b-a+d-c},&c\le x\le d
\\
\frac{2}{b-a+d-c}\cdot\frac{b-x}{b-d},&d<x\le b
\\
0,&\mathrm{otherwise}
\end{cases}
$$

#4. 균등분포 합성곱의 Python 구현
#4-1. np.convolve()
Python에서 합성곱은 np.convolve(fx,fy)로 구현할 수 있는데, fx와 fy자리에는 array 또는 list가 들어가는 점을 주의해야 한다.
예를 들어 정상적인 주사위의 눈 $X$와 홀수만 나오도록 조작된 주사위의 눈 $Y$의 합 $Z=X+Y$의 분포를 np.convolve(fx,fy)로 구하는 문제를 생각해보자. 이 경우 이산확률변수 $X$와 $Y$의 분포는 다음과 같이 표현된다.
$$ X\sim \left[ {\begin{array}{} 1&2&3&4&5&6 \\ \frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6} \end{array}} \right] \\[2ex] Y\sim \left[ {\begin{array}{} 1&2&3&4&5&6 \\ \frac{1}{3}&0&\frac{1}{3}&0&\frac{1}{3}&0 \end{array}} \right] $$
분포행렬의 제1행은 확률변수의 관측값이고 제2행은 각 관측값을 가질 확률질량이다. np.convolve()는 2행인 확률질량만을 입력으로 받는다. 따라서 이 문제를 해결하기 위해서는 다음과 같은 코드를 실행시켜야 한다. (각 확률질량 값은 소수점 3자리만 남긴다.)
import numpy as np
fx = np.array([round(i / 6, 3) for i in [1, 1, 1, 1, 1, 1]])
fy = np.array([round(i / 3, 3) for i in [1, 0, 1, 0, 1, 0]])
fz = np.array([round(i, 3) for i in np.convolve(fx, fy)])
print("fx = %s" % fx)
print("fy = %s" % fy)
print("fz = %s" % fz)
코드를 실행시키면 다음과 같은 결과를 얻는다.
fx = [0.167 0.167 0.167 0.167 0.167 0.167]
fy = [0.333 0. 0.333 0. 0.333 0. ]
fz = [0.056 0.056 0.111 0.111 0.167 0.167 0.111 0.111 0.056 0.056 0. ]
결과물인 fz가 어떻게 나왔는지 쉽게 와닿지 않는다. 그렇다면 직접 손으로 계산하며 어떻게 .convolve() 매서드가 작동하는지 알아보기로 하자. 두 신호의 합성곱은 어느 하나를 뒤집어서 겹치는 면적(=확률)을 계산한 것임을 알고있다. 여기서는 fy를 뒤집기로 하자. 이제 fx와 fy를 조금씩 겹쳐가며 fz를 계산해보자. np.convolve()는 대략 다음과 같은 방식으로 작동한다는 사실을 알 수 있다.

$$ Z\sim \left[ {\begin{array}{} 2&3&4&5&6&7&8&9&10&11&12 \\ \frac{1}{18}&\frac{1}{18}&\frac{1}{9}&\frac{1}{9}&\frac{1}{6}&\frac{1}{6}&\frac{1}{9}&\frac{1}{9}&\frac{1}{18}&\frac{1}{18}&0 \end{array}} \right] $$
#4-2. 균등분포의 합성곱 구현
np.convolve() 매서드의 작동원리를 참고해서 두 균등분포의 합성곱을 구해보고, 그래프도 그려보자. $\mathrm{U}[2,4]$와 $\mathrm{U}[3,6]$의 합성곱을 예시로 들어보자.
<hide/>
import numpy as np
import matplotlib.pyplot as plt
n = 6
x = np.arange(1, n + 1, 1)
y = np.arange(1, n + 1, 1)
z = np.arange(2, 2 * n + 1, 1)
def uniform(a, b):
distr = []
name = "U[%s" % a + ",%s]" % b
length = b - a + 1
while len(distr) < n:
distr.append(1)
for i in range(n + 1):
if a <= i <= b:
distr[i - 1] = 1
else:
distr[i - 1] = 0
return np.array(distr), name, length
fx, fxname, fxlength = uniform(2, 4)
fy, fyname, fylength = uniform(3, 6)
fz = np.convolve(fx, fy)
print("fx = %s" % fx + "/%s" % fxlength)
print("fy = %s" % fy + "/%s" % fylength)
print("conv(fx,fy) = %s" % fz + "/(%s" % fxlength + "*%s)" % fylength)
fig, ax = plt.subplots(3, 1)
ax[0].stem(
x,
[i / fxlength for i in fx],
label="%s" % fxname,
linefmt="red",
basefmt=" ",
)
ax[0].set_xticks(x)
ax[0].set_yticks([round(i / fxlength, 2) for i in fx])
ax[1].stem(
y,
[i / fylength for i in fy],
label="%s" % fyname,
linefmt="blue",
basefmt=" ",
)
ax[1].set_xticks(y)
ax[1].set_yticks([round(i / fylength, 2) for i in fy])
ax[2].stem(
z,
[i / (fxlength * fylength) for i in fz],
label="%s" % fxname + "*%s" % fyname + "\n(Convolution)",
linefmt="purple",
basefmt=" ",
)
ax[2].set_xticks(z)
ax[2].set_yticks([round(i / (fxlength * fylength), 2) for i in fz])
for i in range(3):
ax[i].legend(loc="upper right")
ax[i].set_xlim(0, 2 * n + 3)
plt.show()실행 결과:
fx = [0 1 1 1 0 0]/3
fy = [0 0 1 1 1 1]/4
conv(fx,fy) = [0 0 0 1 2 3 3 2 1 0 0]/(3*4)

'확률론과 수리통계' 카테고리의 다른 글
| 평균과 기댓값 (0) | 2022.12.27 |
|---|---|
| Irwin-Hall 분포 (0) | 2022.12.25 |
| 확률변수의 최대, 최소의 분포 (0) | 2022.12.09 |
| 확률변수의 사칙연산의 분포 (0) | 2022.12.08 |
| 합성곱 (0) | 2022.12.01 |



