지난 글에서 구간의 길이가 같은 두 균등분포의 합성곱은 대칭삼각분포임을 보였다. 이번 글에서는 이것을 일반화하여 3개의 균등분포, 4개의 균등분포, 더 나아가 임의의 $n$개의 균등분포에 대한 합성곱 연산이 어떤 결과를 가져다 주는지 알아보자. 이 모든 결과는 Irwin-Hall 분포 한 가지로 나타낼 수 있다.
Irwin-Hall 분포는 다음과 같이 정의되는 분포이다:
$\space$
i.i.d. $X_i\sim\mathrm{U}(0,1)(i=1,2,\cdots,n)$이면 $X:=\sum_{i=1}^{n}X_i$는 모수가 $n$인 Irwin-Hall 분포를 따른다.
$\space$
즉, Irwin-Hall 분포는 서로 독립인 표준균등분포의 합성곱이다. 모수가 $n$인 Irwin-Hall 분포의 확률밀도를 $f_n(x)$이라고 하면, 정의에 의해 $f_1(x)=\mathbf{1}_
{(0,1)}(x)$이다.
그리고 지난 글에서 주사위 눈의 합 문제를 통해 구간의 길이가 같은 두 균등분포의 합성곱은 대칭삼각분포임을 알았다. 따라서 $f_2(x)$는 대칭삼각분포임을 짐작할 수 있다. (삼각분포 참조.) 이번에는 주사위 눈의 합이 아닌 합성곱 공식을 통해 $f_2(x)$를 구해보자.
$$
\begin{split}
f_2(x)&=f_1(x)\ast f_1(x)
\\
&=\int_{-\infty}^{\infty}f_1(x-t)f_1(t)\space dt=\int_{0}^{1}f_1(x-t)\space dt
\\
&=\int_{x-1}^{x}f_1(u)\space du,\space u:=x-t
\\
&=
\begin{cases}
x,&0<x<1
\\
2-x,&1<x<2
\\
0,&\mathrm{otherwise}
\end{cases}
\end{split}
$$
마지막의 정적분을 계산할 때는 다음과 같이 그림을 그리는 것이 좋다. 정적분 값은 그래프 아래의 넓이이므로 기하학적 넓이를 구하는 방식으로 접근하는 것이 간편하다.
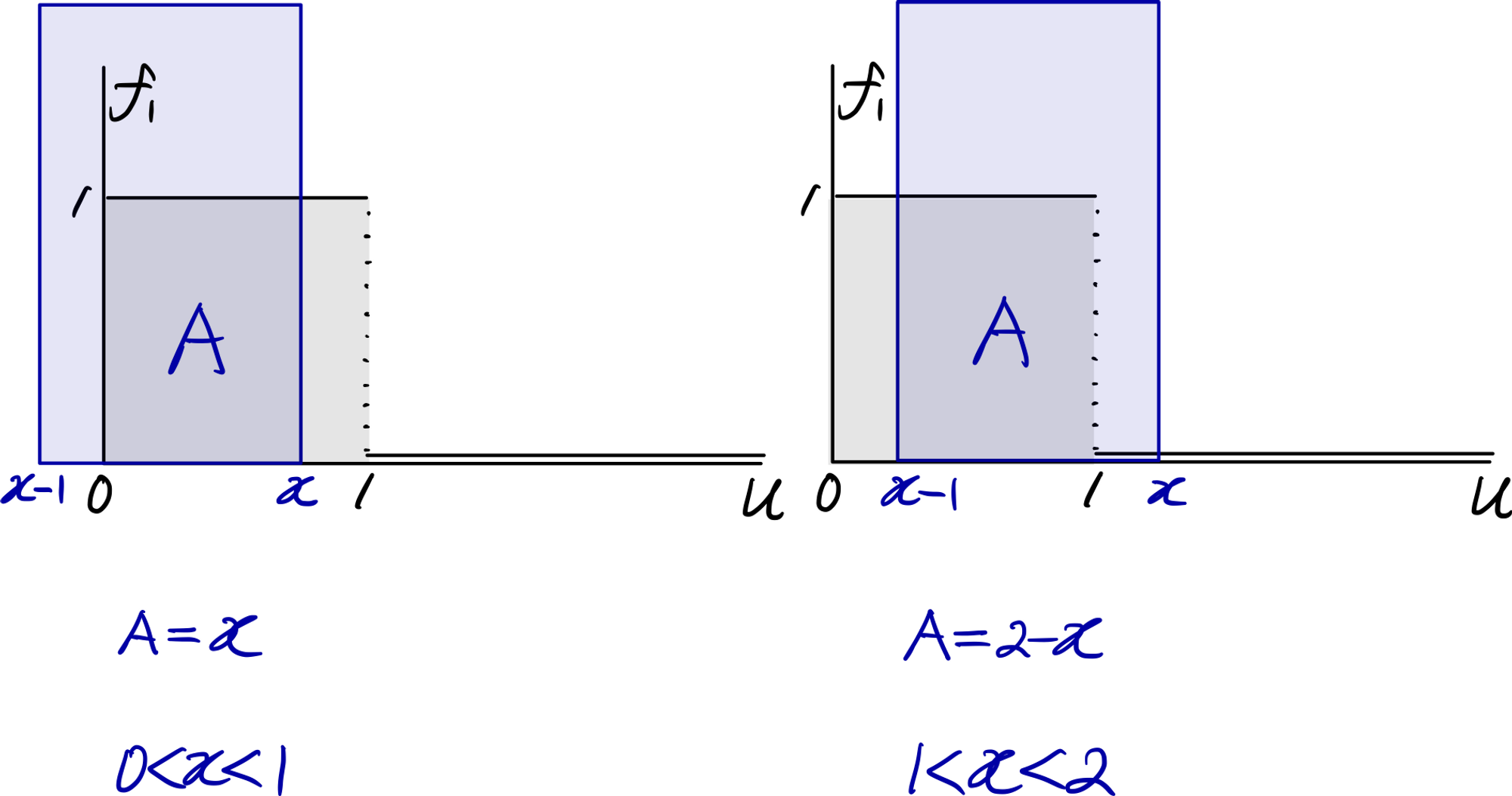
note: 임의의 두 신호에 대해, 한 신호를 뒤집어서 조금씩 이동시킬 때 겹치는 면적을 합성곱이라고 표현하기도 하는데, 그림을 관찰하면 왜 그런 표현을 쓰는지 알 수 있다.
비슷한 방식으로 $f_3(x)$도 구해보자. $f_3(x)$을 계산할 때도 마찬가지로 그림을 통해 이해하는 방법이 좋다.
$$
\begin{split}
f_3(x)&=f_2(x)\ast f_1(x)
\\
&=\int_{-\infty}^{\infty}f_2(x-t)f_1(t)\space dt=\int_{0}^{1}f_2(x-t)\space dt
\\
&=\int_{x-1}^{x}f_2(u)\space du,\space u:=x-t
\\
&=
\begin{cases}
\frac{1}{2}x^2,&0<x<1
\\
\frac{1}{2}[(2-x)x+(x-1)(3-x)],&1<x<2
\\
\frac{1}{2}(3-x)^2,&2<x<3
\\
0,&\mathrm{otherwise}
\end{cases}
\end{split}
$$
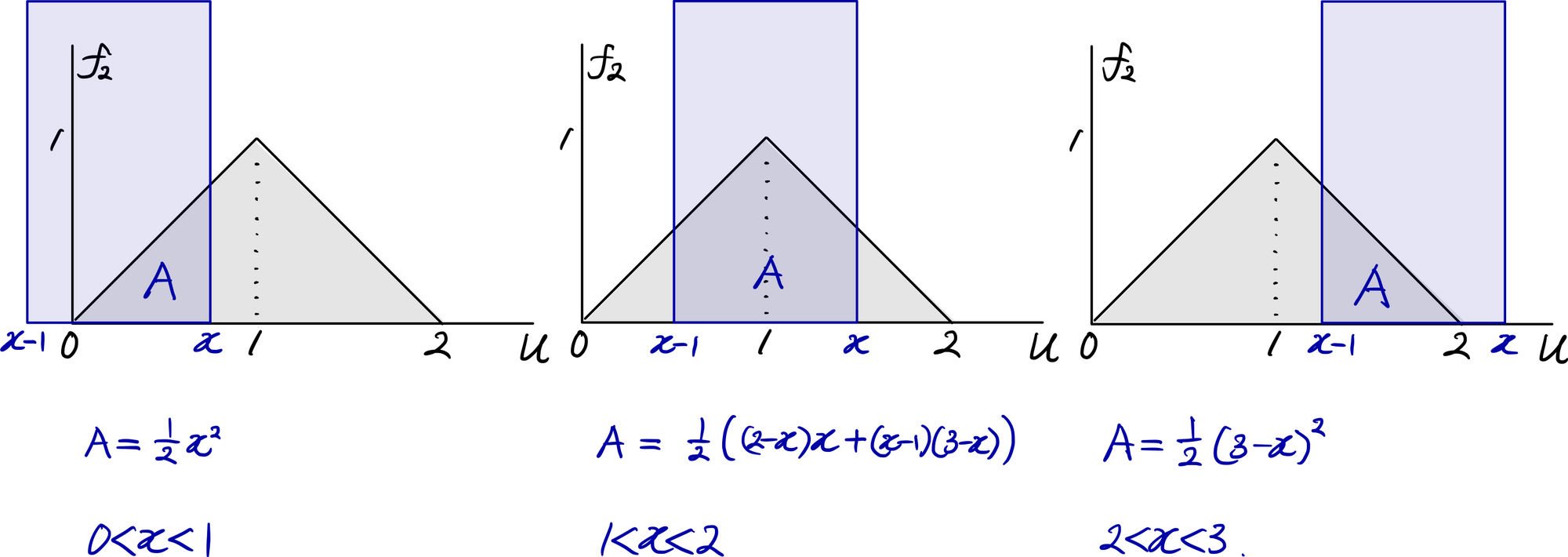
계속해서 비슷한 방식으로 $f_4(x)$, $f_5(x)$역시 얼마든지 구할 수 있다. 식 대신 그래프를 첨부하겠다.
<hide/>
import numpy as np
import matplotlib.pyplot as plt
dt = 0.01
t = np.arange(-30, 30, dt)
a, b = 0, 1
uniform = np.heaviside(t - a, 1) - np.heaviside(t - b, 1)
i, n = 1, 6
convlist = []
alplist = []
ilist = []
while i <= n:
convlist.append(uniform)
alplist.append(1 / (n + 1 - i))
ilist.append(i)
uniform = np.convolve(uniform, uniform, "same") * dt
i = i + 1
for item in range(n):
plt.plot(
t,
convlist[item],
alpha=alplist[item],
label="n=%s" % ilist[item],
color="#000000",
)
plt.legend(fontsize=8, frameon=False, loc="upper right")
plt.xlim([0, 25])
plt.show()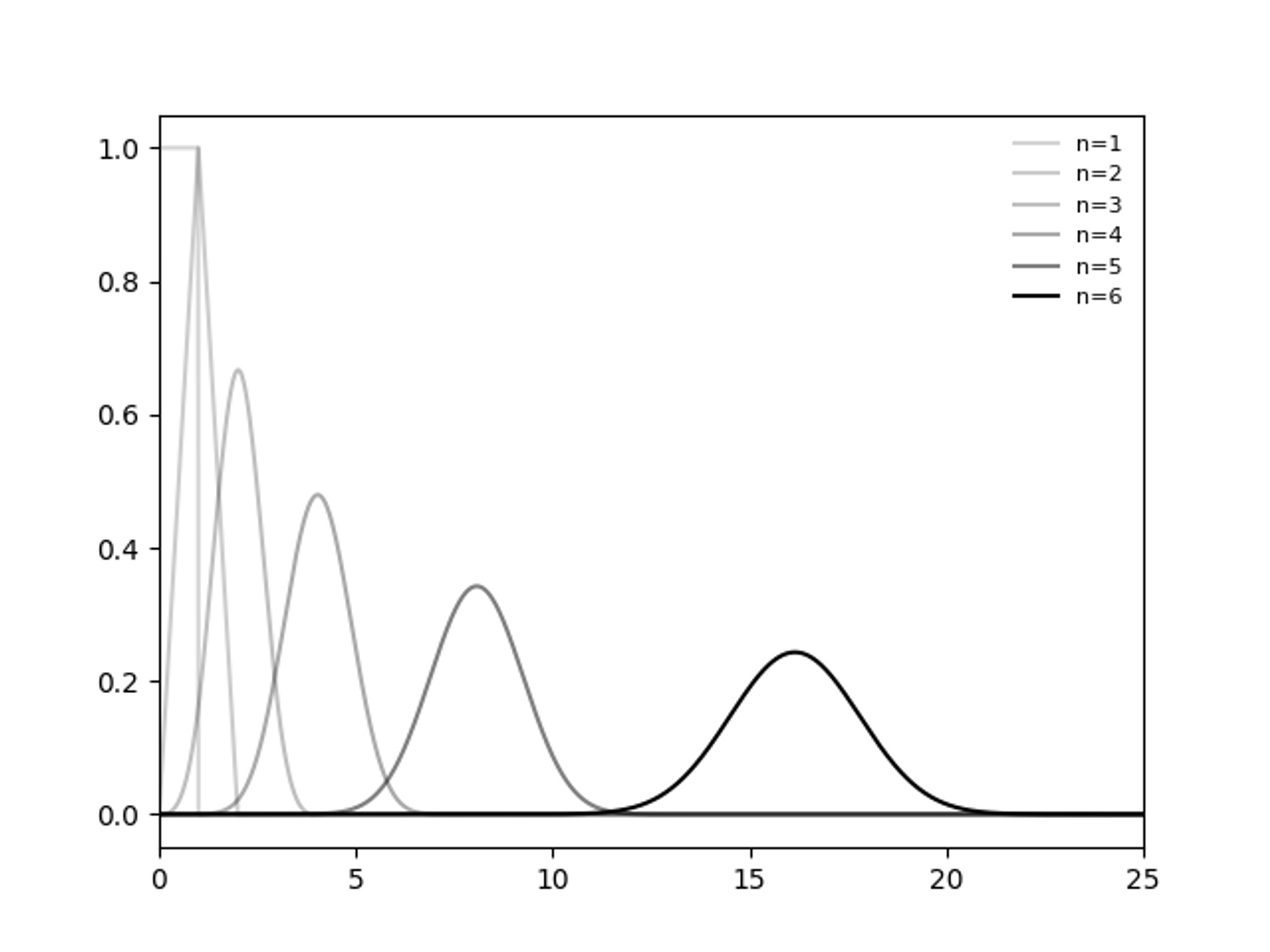
하지만 일반적인 $n$에 대해 $f(x;n)$을 구하려면 이와 같은 방식으로는 어렵다. 일반적인 Irwin-Hall 분포의 PDF는 다음과 같이 주어진다. (https://en.wikipedia.org/wiki/Irwin–Hall_distribution)
$$
f_X(x;n)=\frac{1}{(n-1)!}\sum_{k=0}^{\lfloor x \rfloor}(-1)^{k}{n \choose k}(x-k)^{n-1}
$$
이 식은 $\mathrm{U}(0,1)$을 임의의 $n$번 합성곱한 결과물이다. 식이 매우 복잡하므로, 한꺼번에 일반화를 통해 이해하기보다는 앞서 서술한대로 차근차근 합성곱을 해나가며 Irwin-Hall 분포의 의미를 되새기는 편이 좋겠다.
사실 균등분포의 구간으로서 $(0,1)$이 아닌 임의의 $(a,b)$를 가정해도 무방하다. 이 경우 지난 글에서 보았듯이 여러 균등분포의 구간의 길이가 다를 수 있고, 결과물로서 사다리꼴분포도 얻을 수 있다.
하지만 Irwin-Hall 분포는 그 부품으로서 $\mathrm{U}(0,1)$만을 가정한다. 왜 그럴까? 통계학에서는 많은 변수들이 0에서 1사이의 값을 가진다. 심지어 어떤 변수의 범위가 0부터 1사이가 아닌 경우, 데이터 전처리 과정을 통하여 0부터 1사이의 값을 가지도록 만들기도 한다. (Box-Muller 변환의 ‘정규화’ 참조.) 만약 데이터의 관측값이 특정 값에 편향되지 않는다면, 0과 1사이의 모든 값이 같은 가능성으로 관측될 것이고, 그렇다면 $\mathrm{U}(0,1)$을 따른다고 할 수 있다. 따라서 수많은 균등분포 중에서도 $\mathrm{U}(0,1)$이 특별히 자주 쓰이는 분포이며, 이 분포를 표준균등분포라고 한다.
note: 표준균등분포에서 ‘표준’은 데이터의 ‘표준화’를 일컫는 말이 아니라, 그냥 자주 쓰여서 ‘표준’이라고 하는 것 같다. 실제로 $\mathrm{U}(0,1)$의 평균과 분산을 구해보면 각각 1/2, 1/12로 0과 1이 아니다. 표준정규분포 $\mathrm{N}(0,1)$에서 ‘표준’이 데이터의 표준화를 의미하는 것과 대조적이다.
Irwin-Hall 분포는 단순히 여러개의 균등분포를 합성곱한 결과물이지만, 의외로 중요한 사실이 하나 있는데, $n$이 커질 수록 Irwin-Hall 분포는 정규분포에 가까워진다는 사실이다.
<hide/>
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from UniformSumDistribution import UniformSumDistribution
for n in range(1, 13):
distribution = UniformSumDistribution(n)
start = distribution.ppf(0.0001)
end = distribution.ppf(0.9999)
x = np.linspace(start, end, 100)
y = distribution.pdf(x)
pdf = pd.Series(y, x)
ax = pdf.plot(
kind="line",
label="n=%s" % n,
legend=True,
lw=3,
color="#000000",
alpha=n / 12,
)
ax.set_title("Irwin-Hall Distribution")
plt.show()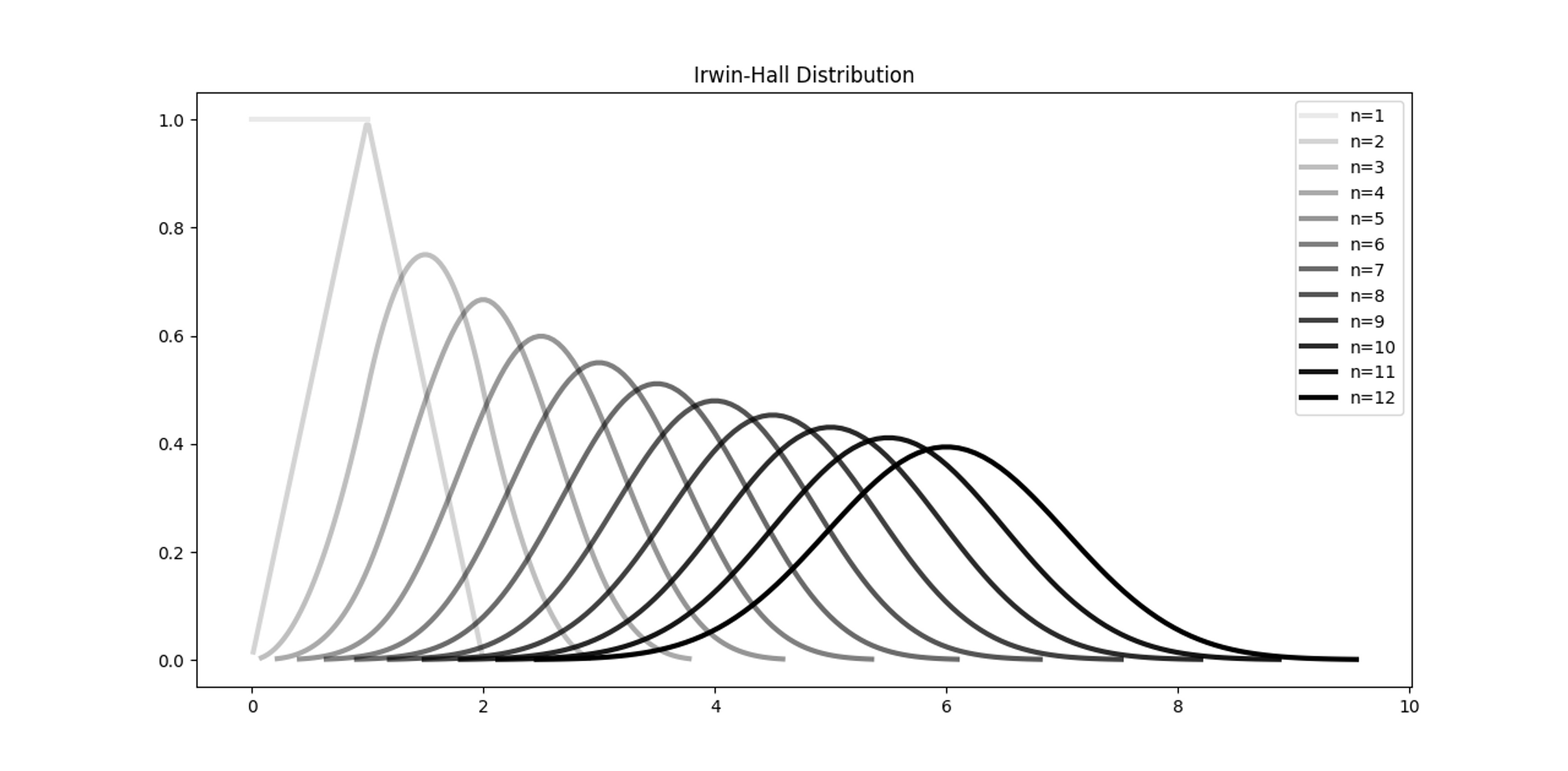
그래프를 보면 $n=12$일 때 정규분포와 매우 닮았다. 실제로 표준정규분포를 따르는 난수를 생성하는 방법 중, 지난글에서 소개한 Box-Muller 변환 외에도 다음과 같이 12개의 균등분포를 따르는 확률변수를 더하고 6을 빼는 방법이 있다.
$$
U_i\sim\mathrm{U}(0,1)\Rightarrow
Z=\sum_{i=1}^{12}U_i-6\sim\mathrm{N}(0,1)
$$
균등분포 $\mathrm{U}(0,1)$의 평균은 $\frac{1}{2}$이고, 분산은 $\frac{1}{12}$이므로, 이 공식은 아래의 중심극한정리(Central Limit Theorem, CLT; 中心极限定理) (추후 작성 예정.)에 $n=12$를 대입하면 얻을 수 있다.
$$
Z=\frac{\sum_{i=1}^{n}U_i-\frac{n}{2}}{\sqrt{n}\sqrt{\frac{1}{12}}}\sim\mathrm{N}(0,1)
$$
물론 $n$이 더 크면 클 수록 좋지만, 일반적으로 $n=12$를 사용하는 이유는 공식의 간편함 덕분이다. 그리고 12정도면 충분히 큰 숫자다.
균등분포를 여러번 합성한 결과물이 정규분포라는 사실은 어떻게 응용될까? 대표적인 것으로 이미지처리 분야에서 가우시안 블러가 있다. 가우시안 블러에서 가우시안은 정규분포의 또 다른 이름인 가우시안 분포에서 따왔다. 어떤 이미지에 가우시안 블러처리를 한다는 것은 기존의 이미지분포에 정규분포를 합성곱한다는 것과 같다.
보통 이미지는 여러개의 픽셀로 구성되며, 1개의 픽셀은 0부터 1사이의 색상치를 갖는다. 초기의 이미지 신호는 딱딱한 사각파의 형태, 즉 균등분포의 형태를 갖고 있다. 여기에 정규분포를 합성곱하면 부드러운 정규곡선 형태의 신호를 얻는다. 정규분포 자체가 이미 수많은 사각파의 합성이므로 사각파 하나가 더 더해진들 큰 영향이 없다는 점을 이용하는 것이다.
'확률론과 수리통계' 카테고리의 다른 글
| 분산과 표준편차 (0) | 2022.12.28 |
|---|---|
| 평균과 기댓값 (0) | 2022.12.27 |
| 삼각분포 (0) | 2022.12.12 |
| 확률변수의 최대, 최소의 분포 (0) | 2022.12.09 |
| 확률변수의 사칙연산의 분포 (0) | 2022.12.08 |



