#1. 평균과 기댓값의 정의
어떤 학생의 기말고사 성적이 다음과 같다고 하자.

이 경우 이 학생의 평균성적은 다음과 같이 계산된다.
$$ 평균성적=\frac{85+92+98}{3}=\frac{85+92+98}{1+1+1} $$
이것은 전형적인 평균의 산출 예시이다. 이 예시에서는 각 과목의 가중치(Weight; 权重)가 1:1:1로 동일함을 가정하고 있다. 즉, 수학에서 100점을 맞느냐 영어에서 100점을 맞느냐가 동일한 취급을 받기 때문에 단순 합산해서 나누는 방식으로 평균이 계산된다.
만약 평정자가 수학점수를 중시하여, 피평정자의 수학점수에만 2배의 가중치를 부여했다고 가정할 경우, 평균은 다음과 같이 계산된다.
$$ 평균성적=\frac{85+92+98\times 2}{1+1+2} $$
즉, 수학에서 100점을 1번 맞은 것을 2번 맞은 것으로 취급하여 총점에 200이 더해진다는 얘기이다. 동시에 과목 숫자도 수학은 2배로 늘어난다. 이와 같이 가중치를 달리하여 산출한 평균을 가중평균(Weighted Mean; 加权平均)이라고 한다. 한편, 위 가중평균의 식을 다음과 같이 변형할 수 있다.
$$ \begin{split} 평균성적&=\frac{85\times 1+92\times 1+98\times 2}{1+1+2} \\ &=\frac{1} {4}\cdot(85,92,98)\cdot(1,1,2) \\ &=(85,92,98)\cdot\left(\frac{1}{4},\frac{1}{4},\frac{2}{4}\right) \end{split} $$
식에서 벡터 $(85,92,98)$은 각 과목의 점수, 즉, 변수이고, 벡터 $\left(\frac{1}{4},\frac{1}{4},\frac{2}{4}\right)$는 각 과목의 가중치를 나타낸다 . 따라서 식의 변형을 통해, 가중평균은 곧 변수벡터와 가중치벡터의 스칼라곱임을 알 수있다.
note: 가중평균을 두 벡터의 스칼라곱으로 나타낼 수 있다는 사실은 엑셀이나 Python을 이용하여 가중평균을 산출할 때 도움이 되는 사실이다. 그리고 공식을 기억하는 데도 도움이 된다.
가중평균이 적극적으로 활용되는 예시가 바로 대학교에서의 평균 평점(Grade Point Average, GPA) 산출이다. 어떤 대학생의 한 학기 수강목록과 각 과목의 평점, 이수단위가 다음과 같다고 하자.

한편, GPA를 산출하는 공식은 다음과 같이 주어진다.
$$ \mathrm{GPA}=\frac{\sum(평점\times이수단위)}{\sum(이수단위)} $$
따라서 이 학생의 이번학기 GPA는 다음과 같이 계산된다. 식을 관찰하면 GPA는 이수단위를 가중치로 삼는 가중평균임을 알 수 있다.
$$ \begin{split} \mathrm{GPA}&=\frac{3.0\times 3+3.3\times 3+3.6\times 4+4.0\times 4}{3+3+4+4} \\ &=\frac{1}{14}\cdot(3.0,3.3,3.6,4.0)\cdot(3,3,4,4) \\ &=(3.0,3.3,3.6,4.0)\cdot\left(\frac{3}{14},\frac{3}{14},\frac{4}{14},\frac{4}{14}\right) \end{split} $$
확률변수의 가중평균도 이 GPA와 비슷한 방식으로 생각할 수 있다. 위 예시에서 이 대학생은 총 14회의 수강 중 3.0점이 3회, 3.3점이 3회, 3.6점이 4회, 4.0점이 4회인 상황과 같다. 그리고 총 14회의 수강 중 3회가 3.3점이라는 것은 3.3점일 확률이 3/14인 것과 동일하다.
이제 이 대학생의 각 과목의 평점을 확률변수 $X$로 두면, 각 과목의 가중치는 $f_X(x)=P(X=x)$이다. 확률변수 $X$의 ‘확률을 가중치로 삼는 가중평균’을 $\mathbb{E}(X)$라고 표시하고, 다음과 같이 정의한다.
$$ \mathbb{E}(X):=\sum xf_X(x) $$
이것은 $X$가 이산확률변수일 경우의 정의이다. $X$가 연속확률변수이면 다음과 같이 정의한다.
$$ \mathbb{E}(X):=\int_{-\infty}^{\infty} xf_X(x)\space dx $$
$X$가 이산인 경우와 연속인 경우를 통틀어 다음과 같이 정의한다.
$$ \mathbb{E}(X):=\int_{-\infty}^{\infty} x\space dF_X(x) $$
그리고 가중평균 $\mathbb{E}(X)$를 간단히 $X$의 평균(Mean; 均值) 또는 기댓값(Expected Value; 期望)이라고 부른다. 엄밀하게는 평균과 기댓값은 다르지만, 지금은 구별하지 않기로 하자. $X$의 기댓값의 다른 기호로는 $EX$, $E(X)$, $E[X]$, $\mathbb{E}[X]$ 등이 있다.
한편, $X$가 아닌 $X$의 변환 $T(X)$의 기댓값은 다음과 같이 구한다.
$$ \mathbb{E}(T(X))=\int_{-\infty}^{\infty}T(x)\space dF_X(x) $$
원래 공식의 $x$를 전부 $T(x)$로 대체한 것이 아님을 주의하자. 뒷부분인 $dF_X(x)$의 $x$는 그대로이다. 이와 같은 이유로 $\mathbb{E}()$를 기댓값 ‘연산자’라고 부를 수 없다.
이 식은 무의식적 통계학자의 법칙(Law of the Unconscious Statistician, LOTUS; 无意识统计学家法则)이라고 불린다. 이 법칙을 이용하면, 변환 후의 확률변수 $T(X)$의 분포 $F_{T(X)}$를 모르더라도 원래 확률변수 $X$의 분포 $F_X$만으로 변환 후의 기댓값 $\mathbb{E}(T(X))$를 계산할 수 있다.
#2. 기댓값의 각종 성질
#2-1. 선형성 관련
정적분과 시그마는 선형성을 가진다. 따라서 기댓값도 선형성을 가진다.
(1) $\mathbb{E}(\mathrm{constant})=\mathrm{constant}$
(2) $\mathbb{E}(aX+bY)=a\mathbb{E}(X)+b\mathbb{E}(Y)$
(3) $a\le X\le b\Rightarrow a\le\mathbb{E}(X)\le b$
#2-2. 독립성 관련
확률의 곱셈과 비슷하게, 서로 독립인 확률변수의 곱의 기댓값을 기댓값의 곱으로 나타낼 수 있다. 독립성이 보장될 때 $\mathbf{X}=(X_1,X_2,\cdots,X_n)$의 결합분포 $f_{\mathbf{X}}(\mathbf{x})$를 주변분포의 곱인 $\prod_{i=1}^{n}f_{X_i}(x_i)$으로 나타낼 수 있음을 생각하면 당연한 사실이다.
(4) $X_i(i=1,2,\cdots,n)$가 독립이면 $\mathbb{E}\left(\prod_{i=1}^{n}X_i\right)=\prod_{i=1}^{n}\mathbb{E}(X_i)$
#2-3. 조건부 관련
한편, 조건부분포가 있듯이 조건부 기댓값(Conditional Expectation; 条件期望)도 생각해볼 수 있다. $X=x$인 조건 하의 $Y$의 기댓값을 다음과 같이 정의한다. 주의할 점은 이 경우 $\mathbb{E}(Y\mid x)$는 $x$에 관한 함수라는 것이다. 따라서 동시에 확률변수이기도 하다.
$$ \begin{split} \mathbb{E}(Y\mid x)&:=\mathbb{E}(Y\mid X=x) \\ &=\sum_{y}yP(Y=y\mid X=x) \\ &=\frac{\sum_{y}yP(X=x,Y=y)}{P(X=x)} \end{split} $$
note1: $\mathbb{E}(Y\mid X=x)$가 $x$에 관한 함수이자 확률변수라는 사실은 놓치기 쉬우며 매우 매우 중요하므로 다시한번 강조. 이 사실은 후술할 전체 기댓값의 법칙을 유도할 때의 핵심사항이다.
note2: 조건부 기댓값의 정의를 보면, 원래 기댓값을 계산할 때 가중치의 역할을 하는 확률만 조건부 확률로 고친 것임을 알 수 있다. 나머지는 변하지 않는다. 따라서 위와 같이 $\mathbb{E}(Y\mid x)$를 구하려는 경우 시그마는 $y$에 관한 것으로 한다. $\mathbb{E}(Y)$를 구할 때 시그마는 $y$에 관한 것이기 때문이다. 마찬가지로 $\mathbb{E}(X\mid y)$를 구할 때는 $x$에 관한 시그마를 쓸 것이다. 원래 $\mathbb{E}(X)$를 구할 때 $x$에 관한 시그마를 쓰기 때문이다.
조건부 기댓값은 조건부확률과 비슷하게 다음과 같은 성질을 갖고 있다.
(5) $X\perp Y$이면 $\mathbb{E}(Y\mid x)=\mathbb{E}(Y)$
그리고 전체확률의 법칙이 있듯이 전체 기댓값의 법칙(Law of Total Expectation; 全期望法则)이 있다. 우선 다음 등식이 성립함을 받아들여야 한다.
$$ \mathbb{E}[\mathbb{E}(Y\mid x)]=\sum_{x}\mathbb{E}(Y\mid x)P(X=x) $$
앞서 강조했던 $\mathbb{E}(Y\mid x)$가 $x$의 함수라는 사실과, 지난글에서 언급한 무의식적 통계학자의 법칙을 떠올린다면, 이 등식이 성립한다는 것을 당연하게 받아들일 수 있다. 계속 익숙하지 않다면 ($\mathbb{E}(Y\mid x)$ 대신 $g(x)$를 넣어보자.)
이제 전체확률의 법칙을 떠올려보자. 표본공간 $\Omega$의 분할 $\lbrace X=x\rbrace$를 정의하고, $P(Y=y)$를 구하면
$$ P(Y=y)=\sum_{x}P(Y\mid x)P(X=x) $$
위에서 언급한 등식이 전체 기댓값의 법칙이라고 불리려면 $\mathbb{E}[\mathbb{E}(Y\mid x)]=\mathbb{E}(Y)$이면 좋을 것 같다. 이제 이 사실을 유도해보기로 하자.
$$ \begin{split} \mathbb{E}[\mathbb{E}(Y\mid x)] &=\sum_{x}\mathbb{E}(Y\mid x)P(X=x) \\ &=\sum_{x}\sum_{y}yP(Y=y\mid X=x)P(X=x) \\ &=\sum_{x}\sum_{y}yP(X=x,Y=y) \\ &=\sum_{y}\sum_{x}yP(X=x,Y=y)\cdots(\ast) \\ &=\sum_{y}y\sum_{x}P(X=x,Y=y) \\ &=\sum_{y}yP(Y=y) \\ &=\mathbb{E}(Y) \end{split} $$
note1: 유도과정에서 $(\ast)$부분이 중요하다. 이산일 경우 시그마의 자리를 바꾸는 것은 연속일 경우 정적분의 순서를 바꾸는 것으로 표현된다. 푸비니 정리(Fubini’s Theorem; 富比尼定理)라고 한다.
note2: 수학적인 유도 외에도, $\mathbb{E}(Y)=\mathbb{E}[\mathbb{E}(Y\mid x)]$라는 사실을 직관적으로 받아들일 수도 있다. $\mathbb{E}(Y)=\sum_{x}\mathbb{E}(Y\mid x)P(X=x)$에서 우변의 의미는 $P(X=x)$를 가중치 삼아 $g(x)=\mathbb{E}(Y\mid x)$라는 확률변수의 기댓값을 구하는 것이다. 따라서 우변을 $\mathbb{E}[\mathbb{E}(Y\mid x)]$로 대체할 수 있다.
따라서 전체 기댓값의 법칙은 다음과 같이 두 가지의 버전으로 요약된다.
(6) $\mathbb{E}(Y)=\sum_{x}\mathbb{E}(Y\mid x)P(X=x)$
(7) $\mathbb{E}(Y)=\mathbb{E}[\mathbb{E}(Y\mid x)]$
(7)은 기댓값에 관한 식을 정리할 때 ‘$\mathbb{E[]}$’와 ‘$\mid x$’를 한방에 날려버릴 수 있는, 또는 덧붙일 수 있는 좋은 법칙 같다. ‘조건부 기댓값의 기댓값은 무조건 기댓값’이라고 기억해두자.
한편, 조건부 기댓값을 다룰 때 이미 알고 있는 사실은 상수 취급하여 밖으로 끄집어 낼 수 있다. $g(x)=\mathbb{E}[Y\mid X=x]$에 대해,
(8) $\mathbb{E}[h(X)Y\mid X=x]=h(x)\mathbb{E}[Y\mid X=x]=h(x)g(x)$
이 성질을 이해하기 위해 기댓값 $\mathbb{E}[h(X)Y\mid X=x]$을 계산하는 과정을 머릿속에 그려보자. 우선 간단하게 $h(X)=X$로 두고 해보고, 그 다음에 임의의 $h(X)$로 확장시키자.
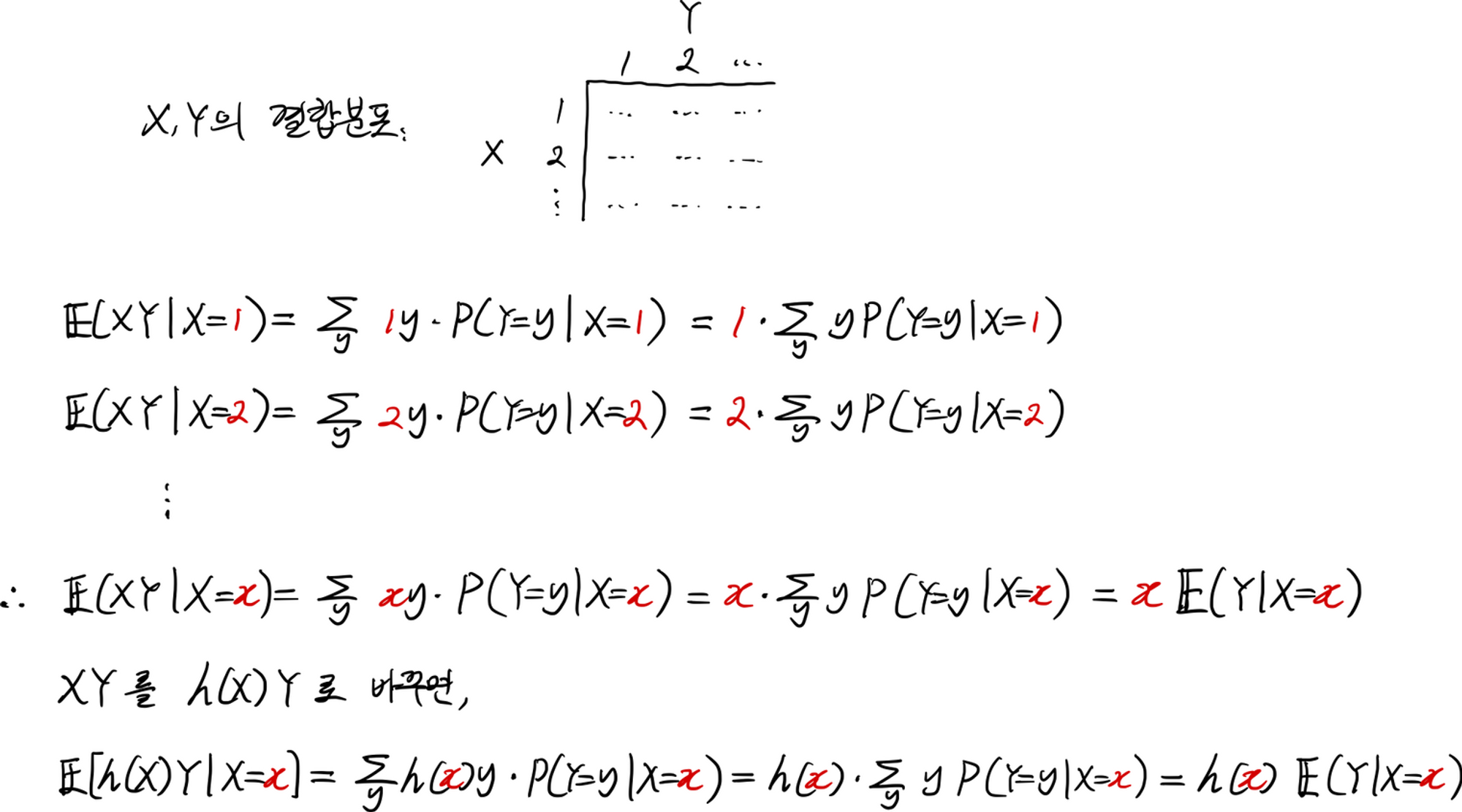
계산과정에서 $h(X)$는 상수취급되고, 시그마의 선형성에 의해 밖으로 끄집어 낼 수 있음을 알 수 있다. $X=x$라는 조건이 알려졌으므로 $h(X)=h(x)$로 값이 고정이 되고, 고정이 됐다는 것은 상수취급을 받는다는 것을 의미한다. 따라서 이 공식을 ‘Pulling out known factors’라고 표현한다. 물론 $\mathbb{E}[h(X)Y\mid X=x]$는 여전히 $x$의 함수이다. $x=1$일 수도 있고, $x=2$일 수도 있다. $x=1$인 경우, 그 값은 $\mathbb{E}[h(1)Y\mid X=1]=h(1)\mathbb{E}[Y\mid X=1]=h(1)g(1)$일 것이다.
'확률론과 수리통계' 카테고리의 다른 글
| 공분산 (0) | 2023.01.01 |
|---|---|
| 분산과 표준편차 (0) | 2022.12.28 |
| Irwin-Hall 분포 (0) | 2022.12.25 |
| 삼각분포 (0) | 2022.12.12 |
| 확률변수의 최대, 최소의 분포 (0) | 2022.12.09 |



