Three-Line Summary!
- Priority queue: a data structure where elements have priorities.
- Heap: a special case of a CBT, used for implementation of a priority queue.
- Complete binary tree (CBT): a special case of a binary tree.
Binary Tree

A binary tree is a hierarchical data structure where each node can have at most two children.
- The two children are called the left child and the right child.
- If a binary tree has $k$ levels, the maximum number of nodes at level $k$ is $2^k$, where $k=0,1,2,\cdots$
Full Binary Tree
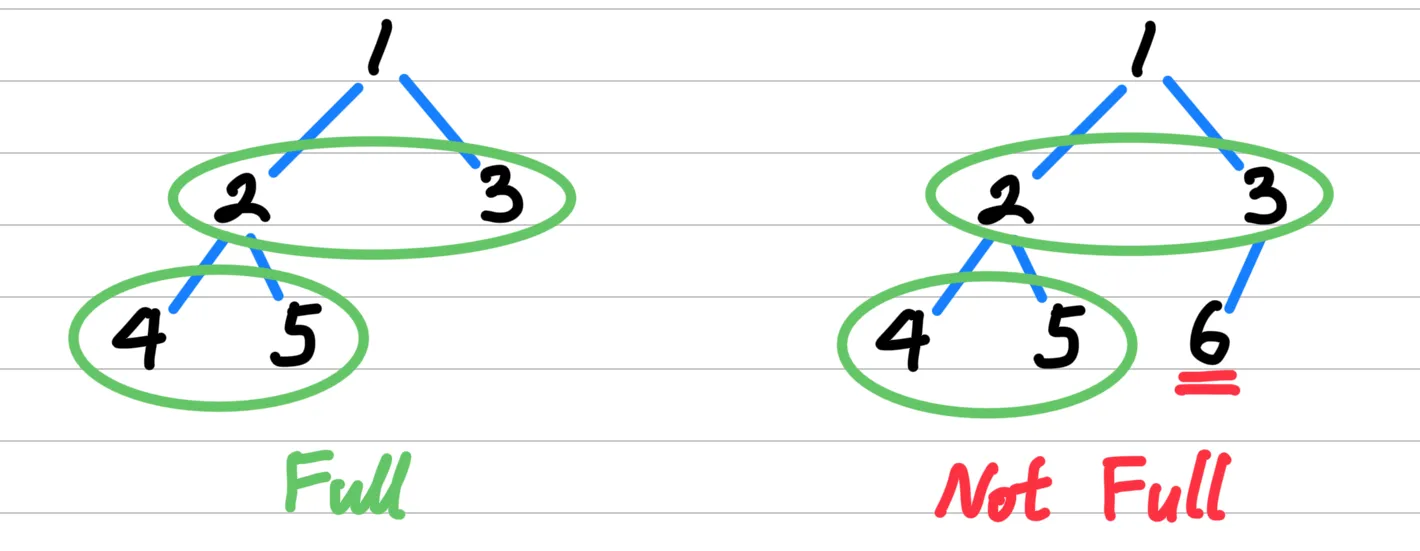
A full binary tree is not the main focus of this article, but it is important to define it to avoid confusion.
A binary tree is full if every node has either 0 or 2 children.
- In other words, if any node has exactly one child (either left or right), then the tree is not a full binary tree.
Complete Binary Tree
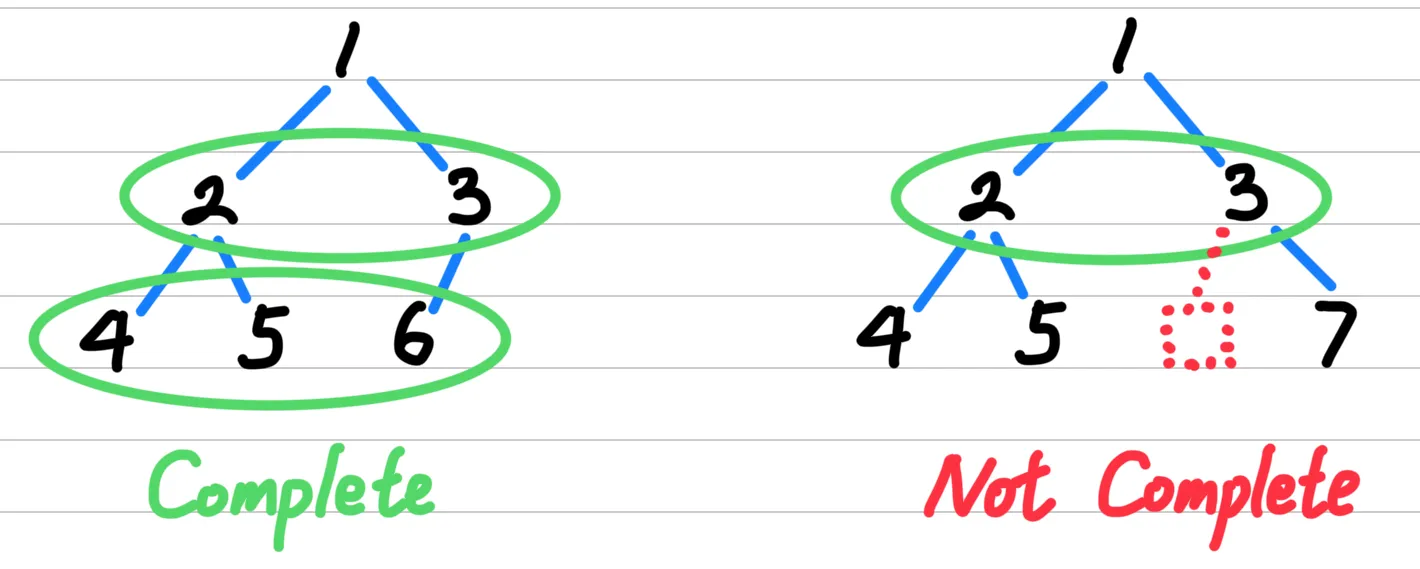
A complete binary tree (CBT) is the main topic of this article. It satisfies the following conditions:
- All levels, except possibly the last, are completely filled with nodes.
- In the last level, nodes must be filled from left to right without any gaps.
Why is a CBT Important?
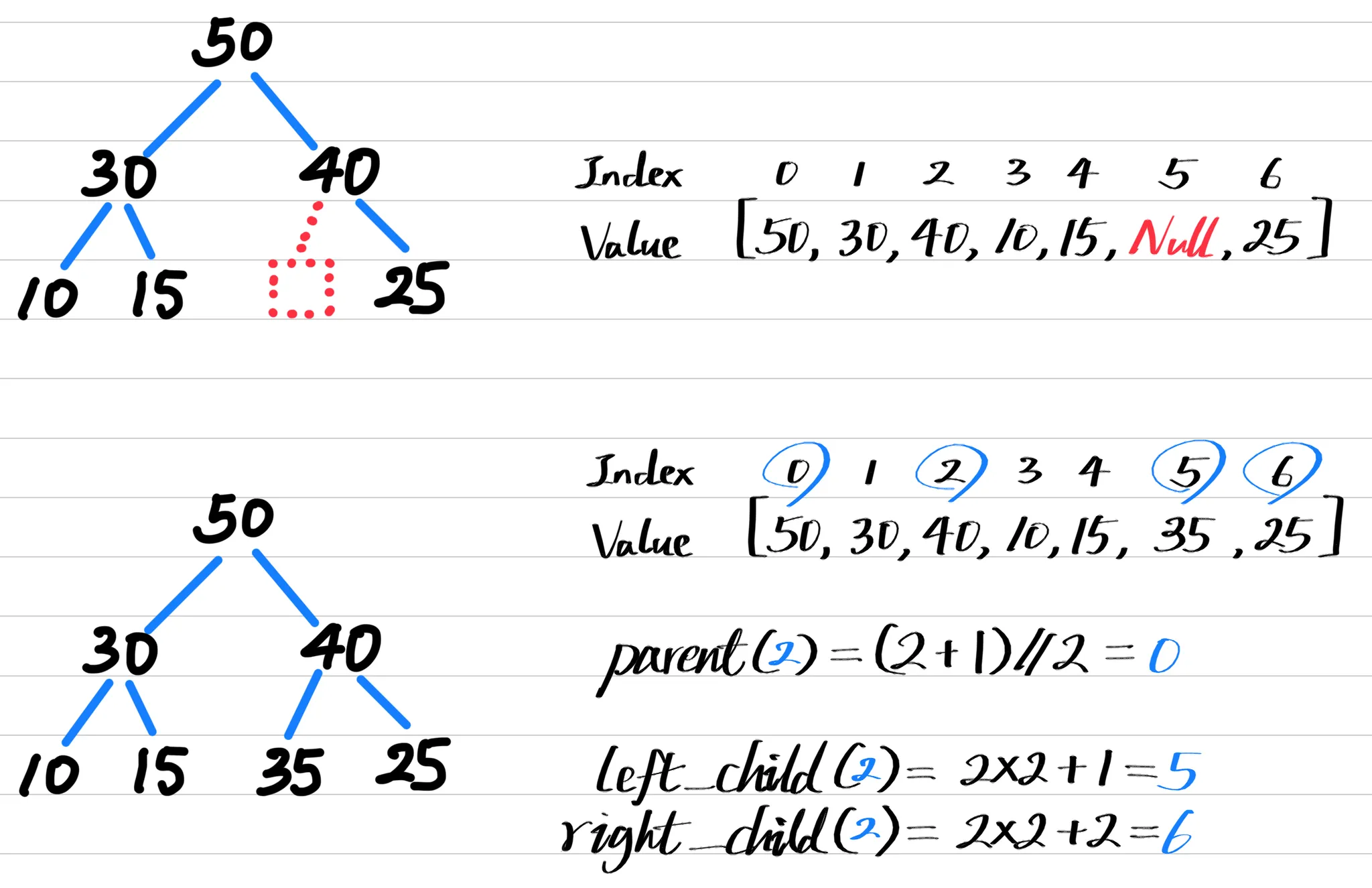
Binary trees can be represented using arrays. Note that there are $2^k$ spaces for nodes at each level. Empty spaces are stored as null values in the array.
CBTs can be stored in an array without using null values, since there is no gap between nodes due to its properties. This allows efficient indexing (0-based) of parent and child nodes in $O(1)$ time complexity, using simple formulas below:
- parent(i) = (i + 1) // 2
- left_child(i) = 2*i + 1
- right_child(i) = 2*i + 2
Heap = Special Case of CBT
A CBT can be classified into three categories based on whether it satisfies the heap property:
- Max-Heap: A CBT where parent ≥ children.
- Min-Heap: A CBT where parent ≤ children.
- Not a Heap: A CBT that does not follow the heap property.
Why is a Heap Useful?
Heap always keeps the max/min at the root, making it $O(1)$ for retrieval, while a CBT that is not a heap requires $O(n)$.
- Min-Heap allows efficient extraction of the minimum value in $O(1)$ time, since the root always (index 0) contains the minimum value.
- Max-Heap allows efficient extraction of the maximum value in $O(1)$ time, since the root always (index 0) contains the maximum value.
Heap as Priority Queue
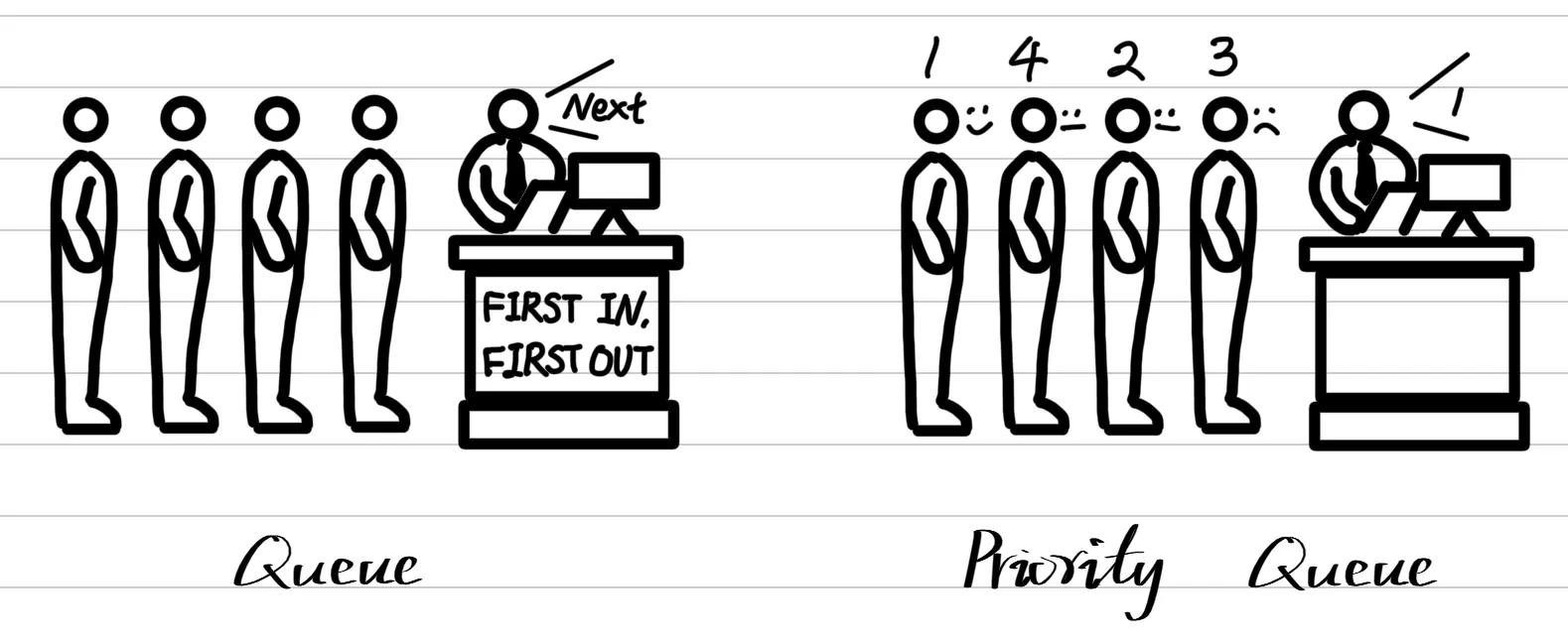
A priority queue is an abstract data type (ADT) where elements are assigned priorities and are dequeued based on their priority. (It does not follow the FIFO order.)
A min-heap can be used to implement a priority queue where the smallest element has the highest priority.
Code
import heapq # Python's built-in heap (min-heap)
pq = [] # Empty list, used for priority queue
# Insert elements assigning priorities
heapq.heappush(pq, 5) # Insert 5
heapq.heappush(pq, 2) # Insert 2
heapq.heappush(pq, 8) # Insert 8
heapq.heappush(pq, 1) # Insert 1 (highest priority)
# Extract elements in priority order
print(heapq.heappop(pq)) # Output: 1 (highest priority)
print(heapq.heappop(pq)) # Output: 2
print(heapq.heappop(pq)) # Output: 5
print(heapq.heappop(pq)) # Output: 8
Using pq.append(item), we are simply adding elements to a regular list, which does not maintain any order. If we later process elements using pq.pop(), it will remove and process the last inserted element first, which behaves like a stack (LIFO order).
- When using heapq.heappush(pq, item), it ensures that the smallest element is always at the top of the heap.
'Algorithm' 카테고리의 다른 글
| Breadth-Frist Search (BFS) vs Depth-First Search (DFS) (0) | 2025.02.15 |
|---|---|
| Stack vs Queue (0) | 2025.02.13 |
| Union-Find Algorithm (0) | 2025.02.12 |
| Dijkstra’s Algorithm (0) | 2025.02.11 |



