2022.10.05 - [확률론과 수리통계] - 이산확률변수, 확률질량함수, 이산분포, 누적분포함수
2022.10.14 - [확률론과 수리통계] - 연속확률변수, 확률밀도함수, 연속분포, 누적분포함수
연속확률변수에 대해 어느정도 공부하고 나서 궁금증이 생겼다. 어떤 연속확률변수의 확률분포를 나타내는 함수를 왜 확률밀도함수(Probability Density Function, PDF; 概率密度函数)라고 이름 붙였으며, 확률밀도함수의 적분이 왜 특정 구간의 확률 값이 되는 것일까? 확률 ‘밀도’라고 하니, ‘질량’과 ‘부피’가 생각난다. 확률밀도함수는 물리학의 이 개념들과 모종의 연관이 있지 않을까?
#1. 물리학에서의 밀도
이 질문에 답하기 위해, 다음 그림과 같이 어떤 각목 형태의 물체를 생각하자.

이 각목의 밀도는 $\rho = 0.1\space\mathrm{kg/m^3}$으로 주어진다. 부피를 $V = 100\space\mathrm{m^3}$라 하면, 질량 $m$을 다음과 같이 계산할 수 있다.
$$
\begin{split}
m &= \rho V
\\
&= 0.1\space\mathrm{kg/m^3}\cdot 100\space\mathrm{m^3}
\\
&= 10\space\mathrm{kg}
\end{split}
$$
note: $1\space\mathrm{m^3}$의 작은 공간당 어떤 물질이 $0.1\space\mathrm{kg}$만큼 있다고 생각해보자. 그러면 $100\space\mathrm{m^3}$의 공간에서는 $10\space\mathrm{kg}$만큼 있다고 생각할 수 있다.
이것은 각목의 밀도가 $\rho = 0.1\space\mathrm{kg/m^3}$라는 일정한 값으로 주어졌을 때의 계산이다. 이제 각목을 다음 그림과 같이 이질적인 두 부분으로 나누자.
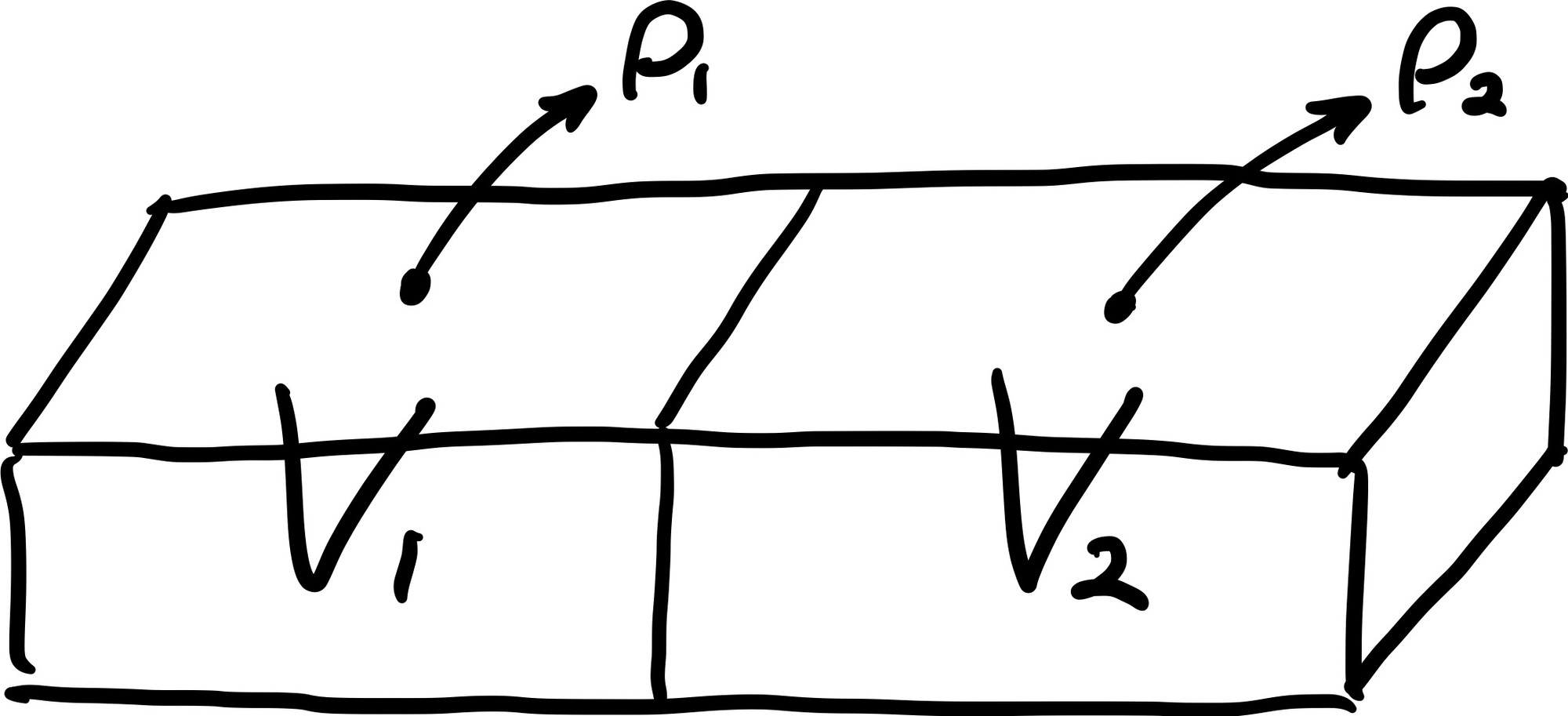
각 부분의 밀도를 $\rho_1 = 0.1\space\mathrm{kg/m^3}$, $\rho_2 = 0.2\space\mathrm{kg/m^3}$, 부피를 $V_1 = 40\space\mathrm{m^3}$, $V_2 = 60\space\mathrm{m^3}$이라고 했을 때, 이 각목의 질량은 다음과 같이 계산된다.
$$
\begin{split}
m &= \rho_1 V_1 + \rho_2 V_2
\\
&= 0.1\space\mathrm{kg/m^3} \cdot 40\space\mathrm{m^3} + 0.2\space\mathrm{kg/m^3} \cdot 60\space\mathrm{m^3}
\\
&= 4\space\mathrm{kg} + 12\space\mathrm{kg}
\\
&= 16\space\mathrm{kg}
\end{split}
$$
각목을 3부분으로 나누면, 각목의 질량은 $\rho_1 V_1 + \rho_2 V_2 + \rho_3 V_3$이고, $n$부분으로 나누면 $\sum_{i=1}^n \rho_i V_i$일 것이다. 각목을 아주 많은 부분(i.e., $n \rightarrow \infty$)으로 쪼개면, 질량을 다음과 같이 기술할 수 있다.
$$
m = \lim_{n \rightarrow \infty} \sum_{i=1}^n \rho_i V_i = \iiint_V \rho(x,y,z)\space\mathrm{d} V
$$
note: 각목을 아주 많은 부분으로 쪼갤 때, 각 부분은 미세한 부피 $\mathrm{d}V$를 갖는다. 또한, 잘게 쪼개는 과정에서 각목의 밀도는 더 이상 상수가 아니고, 어느 위치에 있는가에 따라서 변할 것이다. 즉 밀도는 3차원 위치벡터 $(x,y,z)$의 함수인 $\rho(x,y,z)$이고, 질량은 이 밀도함수를 $V$라는 공간에서 적분한 값이다.
3차원의 물체인 각목의 질량을 기술했으니, 이제 ‘2차원의 물체’인 종이의 질량을 기술해보자. 간단하다. 넓이를 $A$로 놓으면, 종이의 질량은 다음과 같다.
$$
m = \lim_{n \rightarrow \infty} \sum_{i=1}^n \rho_i A_i = \iint_A \rho(x,y)\space\mathrm{d} A
$$
같은 방식으로, ‘1차원의 물체’인 실의 질량은 길이를 $L$로 놓고, 다음과 같이 나타내자.
$$
m = \lim_{n \rightarrow \infty} \sum_{i=1}^n \rho_i L_i = \int_L \rho(x)\space\mathrm{d} L
$$
지금까지의 사고과정을 다음과 같이 그림으로 요약하자.

#2. 확률밀도함수 vs 밀도함수
연속확률변수 $X$가 구간 $[a,b]$안의 값을 가질 확률을 $P(a \leq X \leq b) = \int_{a}^{b} f(x)\space\mathrm{d}x$로 나타낼 수 있을 때, 이 $f(x)$를 확률밀도함수라고 했다.
1차원 물체의 질량 $\int_L \rho(x)\space\mathrm{d} L$은 확률밀도함수의 정적분인 $\int_{a}^{b} f(x)\space\mathrm{d}x$와 비슷하다. 그래서 확률밀도함수 $f(x)$에서 ‘밀도’라는 말은 일종의 비유라고 볼 수 있다. $\rho$대신 $f$를 쓴 것 뿐이다.
note: $L$을 집합 $\lbrace
x \mid a \leq x \leq b
\rbrace$으로 생각하자.
이 비유에 따르면, $P(a \leq X \leq b)$는 ‘확률질량’이다. 그런데 ‘확률질량’이라 하지 않고 확률 값 또는 확률이라고 하는 것 뿐이다. 또한, 연속확률변수 $X$가 특정한 값 $x$를 취할 확률 $P(X=x)$를 굳이 표현하자면 ‘미세한 확률질량’ $f(x)\space\mathrm{d}x$가 되며, 그 값은 0에 가깝다. 구간 $[a,b]$안에서 이 $f(x)\space\mathrm{d}x$들을 모두 더한 값이 곧 $P(a \leq X \leq b) = \int_{a}^{b} f(x)\space\mathrm{d}x$이 된다.
note: 이산확률변수의 경우 $P(X=x) = f(x)$를 확률질량함수(Probability Mass Function, PMF; 概率质量函数)라고 부르는데, 여기서는 $\mathrm{d}x$같은 것을 고려할 필요가 없다. 애초에 확률질량함수의 정의 자체가 연속확률변수와 다르기 때문이다. ($\mathrm{d}x$가 1이 된 것이 결코 아니다.) 이름 자체는 마음에 든다. 확률밀도함수의 비유를 생각해 보면, 특정 확률 값에 대응하는 것은 확률질량이기 때문이다.
이제 이 비유를 다음과 같이 그림을 그려 확인해보자. 아까의 1차원 물체의 그림에서 각 지점의 밀도 $\rho(x)$를 그대로 세로축으로 나타낸다. 이제 밀도 곡선을 그리자. 아무렇게나 그려도 상관없으나, (다만, 값이 마이너스가 안 된다는 것과 특정 위치에서 두 가지 이상의 다른 밀도가 나올 수는 없는 점만 주의하자.) 여기서는 각목의 중간지점 쯤(그림에서 $x_0$지점)의 밀도가 가장 높고, 그 주위로 갈수록 낮아진다고 하겠다.

아니, 이것은 어디서 보던 모양이 아닌가? 그렇다. $\rho$대신 $f$를 쓰면 우리가 알던 확률밀도함수의 그래프이다. 그림에서 $\rho(x_0)$이 $\rho(x)$의 최댓값이다. $\rho(x_0)$이 질량이 아니라 $x_0$에서의 밀도 값이지만, 그래도 밀도가 높은 쪽은 비교적 질량이 클 것이다. 정확히는 이 $x_0$근방의 질량 $m(x_0 - \epsilon < x < x_0 + \epsilon)$이 비교적 클 것이다. $\epsilon$은 매우매우 작은 양수이다.
마찬가지로 $x_0$에서의 확률밀도함수의 값 $f(x_0)$은 결코 확률 값은 아니지만, 그 값이 클 수록 확률변수가 그 주변 값을 가질 확률 $P(x_0 - \epsilon < x < x_0 + \epsilon)$은 비교적 크다는 것을 나타낼 수는 있다. 그래서 확률밀도곡선의 어떤 지점에서의 높이를 보고, 확률변수가 그 지점에서 값을 가질 ‘확률’이 크다고 표현해도 무리는 아니다.
note: 예를 들어, 흔히 정규분포에서 $X = \mu$일 ‘확률’이 제일 크다고 표현하지만, 사실 연속확률분포에서 모든 $x$에 대해 $P(X=x)=0$이 성립하므로 이는 잘못된 표현이라고 할 수 있다. 확률밀도가 크다고 해야 맞다.
밀도함수의 그래프 아래 넓이는 질량이고, 확률밀도함수의 그래프 아래 넓이는 확률값이다. 다음 그림을 보자. 즉, 질량과 확률은 대응된다.

이제 1차원에서 $\int_L \rho(x)\space\mathrm{d} L$이 $\int_{a}^{b} f(x)\space\mathrm{d}x$에 대응된다는 사실을 알았으니, 2차원에서 $\iint_A \rho(x,y)\space\mathrm{d} A$는 $\iint_{A} f(x,y)\space\mathrm{d}x\mathrm{d}y$에 대응된다고 생각할 수 있고, 같은 방식으로 3변수, 더 나아가 $n$변수 확률밀도함수를 이해할 수 있다.
note: 2변수일 때 $\mathrm{d}A = \mathrm{d}x\mathrm{d}y$, 3변수일 때 $\mathrm{d}V = \mathrm{d}x\mathrm{d}y\mathrm{d}z$임을 기억하자.
#3. 더 생각해볼 점
확률밀도함수는 결국 물리학의 개념으로 비유한 것으로 이해된다. 과학에서 비유(metaphor)란 매우 강력하다. 때로는 현상을 쉽게 설명하는 것에 그칠지 몰라도, 때로는 새로운 무언가를 발견하는 강력한 도구가 될 수도 있다. 과학에서 비유란, source domain을 target domain으로 보내는 mapping이라고 할 수 있겠다. 이제 통계학에서의 확률밀도를 물리학에서 물체의 밀도와 연관지었으니, 물리학세계에서 밀도와 관련된 개념들을 통계학세계로 수입해올 수 있다.
대표적인 것이 모멘트인데, 통계학에서는 적률(moment, 矩)이라고 한다. $n$차 모멘트는 $\int r^n \rho(r)\space\mathrm{d}r$인데, 여기서 $\rho$는 각종 물리량(질량, 힘, 전하 등)의 밀도(또는 주어진 공간 안에서의 분포)를 나타내며, $r$은 그 물리량이 작용하는 위치로 볼 수 있다. 이와 비슷하게, $n$차 적률은 $\int x^n f(x)\space\mathrm{d}x$이고, $f$는 확률변수의 확률밀도(확률변수의 분포)를 나타내며, $x$는 확률변수의 관측 값이다.
다만, 물리학에서의 밀도함수함수를 문자 그대로 끌고 올 수는 없고, 통계학의 세계에서는 모종의 제약이 따른다. 그것은 바로 $\int_{- \infty}^{\infty} f(x)\space\mathrm{d}x = 1$으로, 모든 확률의 합은 1임을 나타낸다. 이 조건을 만족하지 않는 $f(x)$는 결코 확률밀도함수라고 할 수 없다. 즉 확률변수 $X$의 분포를 새로 구축할 때, 아무 함수(e.g., $f(x) = x^2$)나 가져다 쓸 수 없다는 뜻이다.
note: 실제로 어떤 함수의 형태가 마음에 들어 이를 PDF로 삼으려 할 경우, 적절한 상수를 곱하는 방법을 쓴다. 이와 관련된 구체적 예시는 ‘베타분포의 이해’를 참고하면 좋다.
2022.10.02 - [확률론과 수리통계] - 베타분포의 이해


